Formule de règle Simpson, démonstration, exemples, exercices

La Règle Simpson Il s'agit d'une méthode pour calculer, approximativement, des intégrales définies. Il est basé sur la division de l'intervalle d'intégration en une paire de sous-intervalos également espacés.

Les valeurs extrêmes de deux sous-intervalles consécutifs définissent trois points, qui ajuste une parabole, dont l'équation est un polynôme au deuxième degré. 

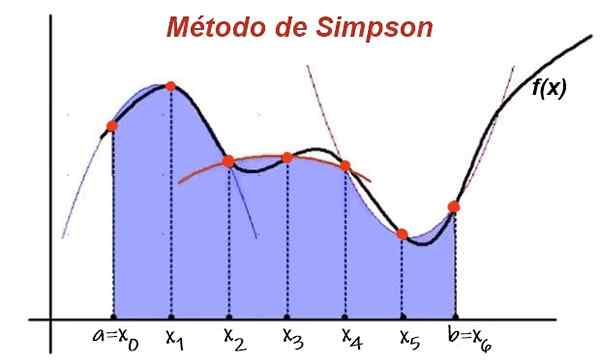
Figure 1. Dans la méthode Simpson, l'intervalle d'intégration est subdivisé en une paire d'intervalles de largeur égale. La fonction est approximée par une parabole dans tous les 2 sous-intervalos et les approches intégrales par la somme de la zone sous les paraboles. Source: UPV.est.

Ensuite, la zone sous la courbe de la fonction dans les deux intervalles consécutifs est approximée par la zone polynomiale d'interpolation. Ajoutant la contribution à la zone sous la parabole de toutes les sous-intervalles successifs, il y a la valeur approximative de l'intégrale.

D'un autre côté, comme l'intégrale d'une parabole peut être calculé de manière algébrique exactement, il est possible de trouver une formule analytique pour la valeur approximative de l'intégrale définie. Est connu comme le Formule Simpson.

L'erreur du résultat approximatif ainsi obtenu diminue dans la mesure où le nombre de subdivisions n est un nombre plus élevé (étant un couple).

En dessous, une expression sera donnée qui permet d'estimer le niveau supérieur de l'erreur d'approche à l'intégrale I, lorsqu'une partition de sous-intervalles réguliers de l'intervalle total [a, b] a été fait [b].

[TOC]

Formule

L'intervalle d'intégration [a, b] est subdivisé en n sous-intervalles avec N étant un couple. La largeur de chaque subdivision sera:

H = (b - a) / n

De cette façon, sur l'intervalle [a, b], la partition est faite:

X0, x1, x2, ..., xn-1, xn

Étant x0 = a, x1 = x0 + h, x2 = x0 + 2h,…, xn-1 = x0 + (n-1) h, xn = x0 + nh = b.

Il peut vous servir: différence entre cercle et circonférence (avec des exemples)

La formule qui permet de calculer approximativement la fonction intégrale et continue définie, et de préférence douce, dans l'intervalle [a, b] est:

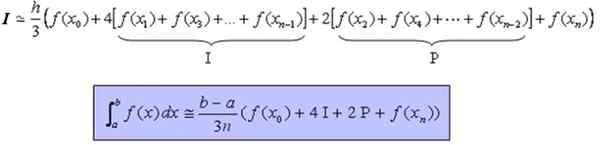
Manifestation

Pour obtenir la formule Simpson, dans chaque sous-intervalle [xi, xi + 2], la fonction F (x) s'approche d'un deuxième degré P (x) polynôme (parabole) qui passe par les trois points: [xi, f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f xi)]; [Xi + 1, f (xi + 1)] et [xi + 2, f (xi + 2)]]].

Alors l'intégrale polynomiale p (x) est calculée dans [xi, xi + 2] qui se rapproche de l'intégrale de la fonction f (x) dans cet intervalle.

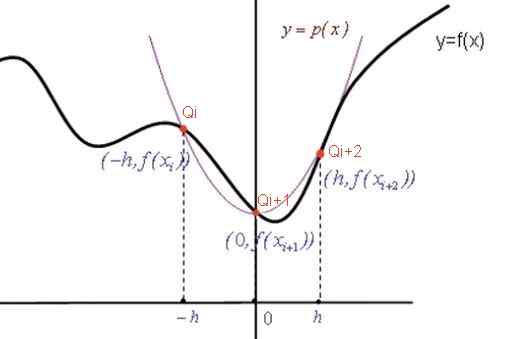Figure 2. Graphique pour démontrer la formule Simpson. Source: F. Zapata.

Coefficients polynomiaux d'interpolation

L'équation de parabole p (x) a la forme générale: p (x) = a x² + B x + c. Comme la parabole passe par les points indiqués en rouge (voir figure), les coefficients a, b, c sont déterminés à partir du système d'équations suivant:

A (-H)² - B h + c = f (xi)

C = f (xi + 1)

A (h)² + B h + c = f (xi + 2)

On peut observer que le coefficient c est déterminé. Pour déterminer le coefficient, nous ajoutons la première et la troisième équation à l'obtention:

2 A H² + 2 c = f (xi) + f (xi + 2).

Ensuite, la valeur de C est remplacée et il est clair:

A = [f (xi) - 2 f (xi + 1) + f (xi + 2)] / (2 h²)

Pour déterminer le coefficient B, la troisième équation du premier est soustraite et B se nettoie:

B = [f (xi + 2) - f (xi)] = 2 h.

En résumé, le polynôme du deuxième degré P (x) qui passe par les points Qi, Qi + 1 et Qi + 2 a des coefficients:

A = [f (xi) - 2 f (xi + 1) + f (xi + 2)] / (2 h²)

B = [f (xi + 2) - f (xi)] = 2 h

C = f (xi + 1)

Calcul de l'intégrale approximative dans [xi, xi + 2]

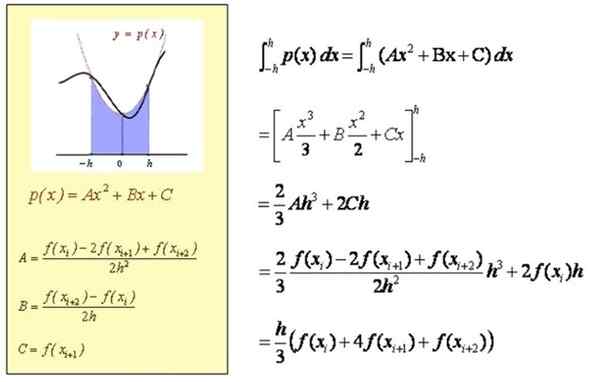
Calcul approximatif de l'intégrale dans [a, b]

Comme cela a déjà été dit, sur l'intervalle d'intégration total [a, b] une partition x0, x1, x2,…, xn -1, xn avec étape h = xi + 1 - xi = (b - (b -) / n, où n est un couple.

Peut vous servir: Erreur d'échantillonnage: formules et équations, calcul, exemples

Ensuite, l'intégrale définie dans l'intervalle total [a, b] est la somme des intégrales dans les sous-intervalles [xi, xi + 2], qui sont abordées par les intégrales des polynômes d'interpolation P (x):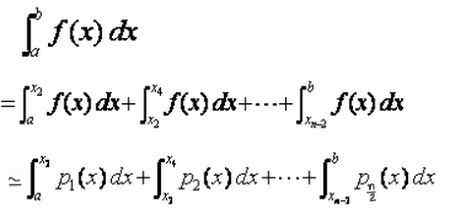

Dans la section précédente, la formule des intégrales polynomiales dans les sous-intervalles a été trouvée. L'application de ce résultat à chaque intégrale a: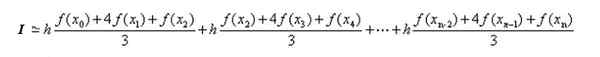

Qui peut être réécrit de manière plus compacte comme suit: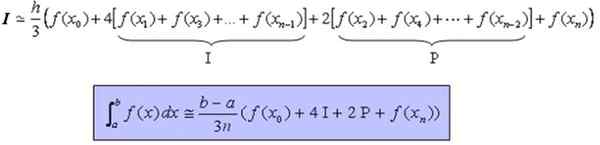

Erreur d'approche

Si la fonction à laquelle vous souhaitez vous intégrer dans l'intervalle [a, b] a dérivé du quatrième ordre, continu dans cet intervalle, il est possible de trouver une formule qui permet de déterminer le niveau d'erreur maximum dans l'approche par des moyens de la Formule Simpson SN Pour la valeur de l'intégrale: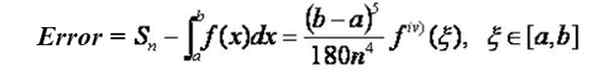

Notez que l'erreur diminue avec la quatrième puissance du numéro de subdivisions d'intervalle. Par exemple, si vous passez de n subdivisions à 2n, alors l'erreur diminue d'un facteur 1/16.

Le niveau d'erreur supérieur obtenu par l'approche Simpson peut être obtenu à partir de cette même formule, remplaçant le quatrième dérivé par la valeur absolue maximale du quatrième dérivé dans l'intervalle [a, b].

Exemples résolus

- Exemple 1

Considérez la fonction f (x) = 1 / (1 + x²). 

Trouvez l'intégrale définie de la fonction f (x) dans l'intervalle [-1, 1] en utilisant la méthode Simpson avec deux subdivisions (n ​​= 2).

Solution 

Est pris n = 2. Les limites d'intégration sont a = -1 et b = -2, alors la partition est comme ceci: 

X0 = -1; X1 = 0 et x2 = +1.

Par conséquent, la formule de Simpson adopte comme suit:

Avec n = 2 → xo = -1, x1 = 0; x2 = 1, donc:

- Exemple 2

Considérez la fonction f (x) = 1 / (1 + x²). 

Trouvez l'intégrale définie de la fonction f (x) dans l'intervalle [-1, 1] par la formule Simpson avec quatre subdivisions (n ​​= 4).

Il peut vous servir: estimation par intervalles

Solution 

Est pris n = 4. Les limites d'intégration sont a = -1 et b = -2, alors la partition est comme ceci: 

X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 et x4 = +1.

La formule de Simpson est établie comme suit:

Intégral ≃ [(b -a) / (3 n)] [f (x0) + 4 i + 2 p + f (xn)]

Pour le cas dans lequel il est appliqué, c'est comme suit:

Intégral ≃ (1- (1)) / (3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)

Intégral ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1,5666

- Exemple 3

Déterminez exactement l'intégrale définie des exemples précédents et faites une comparaison du résultat exact avec ceux obtenus par la formule Simpson dans les exemples 1A et 1B.

Solution 

L'intégrale indéfinie de la fonction f (x) = 1 / (1 + x²) est la fonction Arctan (x).

Lors de l'évaluation des limites d'intégration:

Intégral = arctan (1) - arctan (-1) = π / 4 - (-π / 4) = π / 2 = 1 5708

Si nous comparons le résultat de la solution exacte avec celle obtenue par la méthode Simpson avec n = 2 et n = 4 nous avons:

Pour n = 2, la différence entre la solution exacte et la solution approximative est π / 2 -5/3 = -0959, c'est-à-dire une différence en pourcentage de -0,06%.

Et pour l'approche Simpson avec n = 4, la différence entre la solution exacte et la solution approximative est π / 2 - 47/30 = 0,0041, c'est-à-dire une différence en pourcentage de 0,003%.

Exercice proposé

La méthode de Simpson est adaptée pour être appliquée dans les langages de programmation et les applications informatiques destinées aux calculs mathématiques. Il est proposé au lecteur qui, sur la base des formules données dans cet article, écrivez son propre code dans son programme préféré.

Le chiffre suivant montre un exercice dans lequel la formule Simpson a été mise en œuvre dans Studio smath, logiciel gratuit disponible pour les systèmes d'exploitation les fenêtres et Android.

figure 3. Exemple d'intégration numérique via la règle Simpson à l'aide du logiciel. Source: F. Zapata.

Les références

1. Casteleiro, J. M. 2002. Calcul complet (édition illustrée). Madrid: éditorial ESIC.
2. UPV. Méthode Simpson. Université polytechnique de Valence. Récupéré de: youtube.com
3. Purcell, E. 2007. Calcul de la neuvième édition. Prentice Hall.
4. Wikipédia. Règle Simpson. Récupéré de: est.Wikipédia.com
5. Wikipédia. Interpolation polynomiale de Lagrange. Récupéré de: est.Wikipédia.com