Règle Sarrus

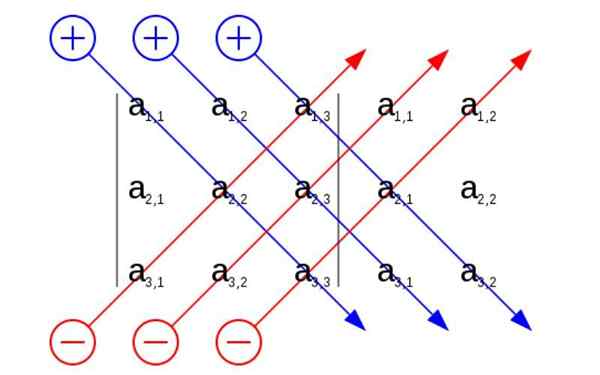
Règle Sarrus. Source: utilisateur: Sevela.P, CC BY-SA 4.0, Wikimedia Commons

Quelle est la règle de Sarrus?

La Règle Sarrus Il s'agit d'une technique pour calculer les déterminants d'une matrice carrée de 3 × 3 ou plus. Ce système permet à la solution d'être plus facilement. Il est également utilisé pour déterminer si les ensembles de vecteurs sont linéairement indépendants et forment la base de l'espace vectoriel.

Ces applications sont basées sur l'invertibilité des matrices. Si une matrice est régulière, son déterminant est différent de 0. S'il est singulier, son déterminant vaut 0. Les déterminants ne peuvent être calculés que dans les matrices carrées.

Pour calculer les matrices de n'importe quel ordre, le théorème de Laplace peut être utilisé. Ce théorème nous permet de simplifier les matrices de dimensions élevées, en sommes de petits déterminants que nous décomposons de la matrice principale.

Indique que le déterminant d'une matrice est égal à la somme des produits de chaque ligne ou colonne, par le déterminant de sa matrice attachée.

Cela réduit les déterminants, de sorte qu'un déterminant du degré n devient déterminant de n-1. Si nous appliquons cette règle de manière successive, nous pouvons obtenir des déterminants de la dimension 2 (2 × 2) ou 3 (3 × 3), où son calcul est beaucoup plus facile.

Règle Sarrus

Pierre Frederic Sarrus (1798-1861) était un mathématicien français. La plupart de ses traités mathématiques sont basés sur des méthodes de résolution des équations et le calcul des variations, dans les équations numériques.

Dans l'un de ses traités, il a résolu l'une des énigmes les plus complexes de la mécanique. Pour résoudre les problèmes des pièces articulées, Sarrus a introduit la transformation des mouvements rectilignes alternatifs, dans des mouvements circulaires uniformes. Ce nouveau système est connu comme le mécanisme Sarrus.

Il peut vous servir: externalisation et internalisation des coûts

La recherche qui lui a donné le plus était celle dans laquelle il a introduit une nouvelle méthode de calcul des déterminants, dans l'article «Nouveles Methody Weep La Résolution des Équations» («Nouvelle méthode pour la résolution des équations»), publiée en 1833. Cette façon de résoudre les équations linéaires est connue sous le nom de règle Sarrus.

La règle Sarrus permet de calculer le déterminant d'une matrice 3 × 3, sans utiliser le théorème de Laplace, introduisant une méthode beaucoup plus simple et plus intuitive. 

Pour pouvoir vérifier la valeur de la règle Sarrus, nous prenons toute matrice de dimension 3:

Le calcul de son déterminant serait fait par le produit de ses principales diagonales, soustrayant le produit des diagonales inverses. Ce serait le suivant:

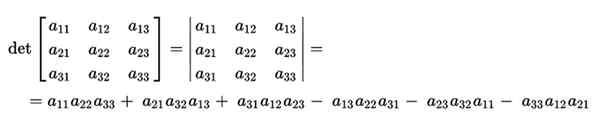
La règle Sarrus nous permet d'obtenir une vision beaucoup plus simple lors du calcul des diagonales du déterminant. Il serait simplifié en ajoutant les deux premières colonnes à l'arrière de la matrice.

De cette façon, il est plus clair sur ses principales diagonales et à laquelle l'inverse, pour le calcul du produit.

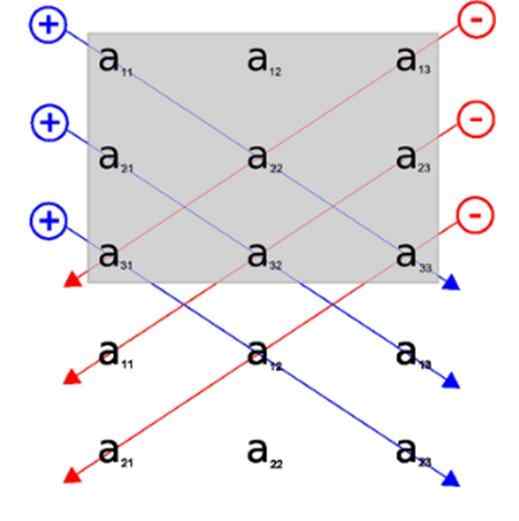
Grâce à cette image, nous pouvons voir l'application de la règle Sarrus, nous incluons les lignes 1 et 2, sous la représentation graphique de la matrice initiale. De cette façon, les principales diagonales sont les trois diagonales qui apparaissent en premier lieu.

Les trois diagonales inverses, à leur tour, sont celles qui apparaissent en premier dans le dos.

De cette façon, les diagonales apparaissent d'une manière plus visuelle, sans compliquer la résolution du déterminant, essayant de savoir quels éléments de la matrice appartiennent à chaque diagonale.

Peut vous servir: des mots quechua traduits en espagnol

Comme il apparaît dans l'image, nous choisissons les diagonales et calculons le produit résultant de chaque fonction. Les diagonales qui apparaissent en bleu sont celles qui s'additionnent. À la somme de ceux-ci, nous soustrayons la valeur des diagonales qui apparaissent en rouge.

Pour que la compression soit plus facile, nous pouvons utiliser un exemple numérique, au lieu d'utiliser des termes algébriques et des termes subterdants.

Si nous prenons une matrice 3 × 3, par exemple:

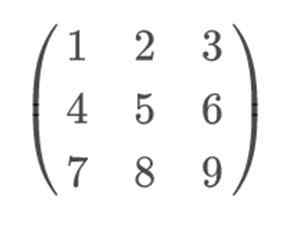
Pour appliquer la règle Sarrus et le résoudre de manière plus visuelle, nous devons inclure respectivement les lignes 1 et 2, comme les lignes 4 et 5. Il est important de maintenir la ligne 1 en 4e position et la rangée 2 dans le 5e. Car si nous les échangeons, la règle de Sarrus ne sera pas efficace.

Pour calculer le déterminant, notre matrice serait la suivante:

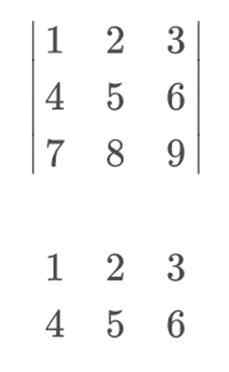
Pour continuer le calcul, nous multiplierons les éléments des diagonales principales. Le descendant qu'ils commencent à gauche porteront un signe positif, tandis que les diagonales inverses, qui sont celles qui commencent à droite, portent un signe négatif.

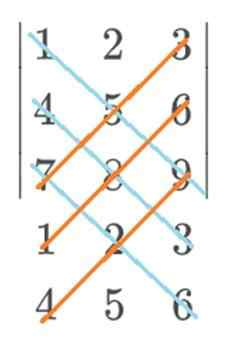
Dans cet exemple, le bleu irait avec un signe positif et le rouge avec un signe négatif. Le calcul final de la règle de Sarrus resterait ainsi:

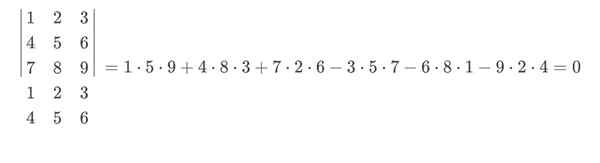
Gars des déterminants

Déterminant de la dimension 1

Si la dimension matricielle est 1, la matrice est de cette manière: a = (a)

Par conséquent, son déterminant serait le suivant: DET (A) = | A | = A

Résumé, le déterminant de la matrice A est égal à la valeur absolue de la matrice A, qui dans ce cas est un.

Déterminant de dimension 2

Si nous allons aux matrices de la dimension 2, nous obtenons des matrices du type:

Peut vous servir: Taumaticgy

Où son déterminant est défini comme:

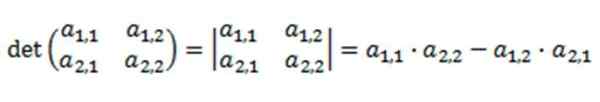
La résolution de ce déterminant est basée sur la multiplication de sa diagonale principale, soustrayant le produit de sa diagonale inverse.

Déterminant de la dimension 3

Si la dimension matricielle est de 3, la matrice résultante serait de ce type:

Le déterminant de cette matrice serait résolu par la règle de Sarrus de cette manière:

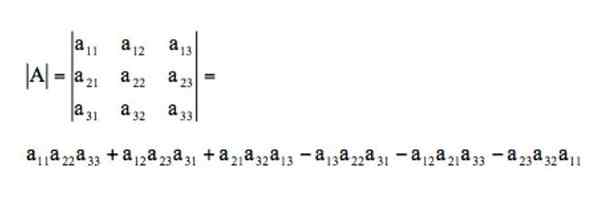
Les références

1. Anthony Nicolaides (1994). Déterminants et matrices. Publication de passage.
2. M. Casteleiro Villalba (2004). Introduction à l'algèbre linéaire. Éditorial ESIC.