Règle de levier

Quelle est la règle du levier?

La règle de levier Il s'agit d'une procédure mathématique qui permet de calculer les fractions, pourcentages ou quantités des phases présentes en équilibre dans un système binaire. Non seulement il est mathématique, mais aussi assez graphique et affirmé, étant très utile dans les calculs physicochimiques et d'ingénierie.

Cette règle s'applique aux diagrammes de phase pour les systèmes binaires, quel que soit le type de système lui-même. C'est-à-dire que les phases peuvent être solides, comme avec les alliages; ou liquide et gazeux, comme nous le voyons dans les systèmes de l'équilibre liquide-vapeur.

Le principe physique et mathématique du levier est également utilisé à des fins chimiques et dans la physique des matériaux. Source: Jimbowley, CC BY-SA 3.0, via Wikimedia Commons

La règle de levier peut être appliquée directement en tenant compte des valeurs graphiques dans l'axe de l'abscisse, où les fractions globales ou les pourcentages de la composante la plus volatile vont généralement, dans le cas des liquides; ou réfractaire, dans le cas des métaux dans leurs alliages.

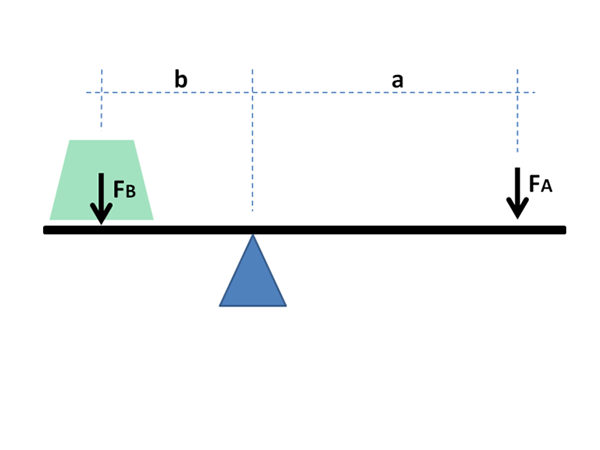
Comme on le verra ci-dessous, son nom est dû à l'immense similitude qu'il a avec les expressions mathématiques qui démontrent l'équilibre entre deux masses situées aux extrémités d'un rocker avec Fulcro.

Les bras de levier doivent équilibrer pour équilibrer les masses des charges; Dans le cas des diagrammes de phase, des fractions et des moles des phases en équilibre de matériau.

Explication

Aspects graphiques

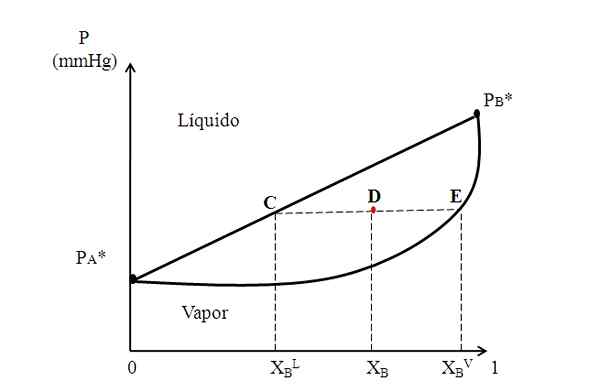Diagramme binaire hypothétique où une ligne de liaison montre les compositions des phases liquide et vapeur. Source: Gabriel Bolívar.

Au milieu du diagramme ci-dessus, nous avons une région où le liquide et la vapeur coexistent; c'est-à-dire la région d'équilibre de vapeur liquide. Au-dessus de cette région, le mélange de A et B sera liquide, et en dessous, il sera de la soude en raison des pressions inférieures.

Maintenant, considérez un mélange avec une composition X_B et dont la pression le positionne au point D. Nous nous étendons du point d une ligne horizontale qui touche la ligne et la courbe sur les côtés, les points d'origine C et E, respectivement. Cette ligne, qui communique les points C, D et E, C-D-E, est celle connue sous le nom de ligne d'union, et en la projetant vers l'axe et doit nous donner la pression du système.

Il peut vous servir: Alcalinité de l'eau: ce qui est, la détermination et l'importance

Ensuite, à partir de ces points, nous dessinons d'autres lignes perpendiculaires à la ligne de liaison, qui jouera l'axe x. Comme le point E repose sur la courbe de vapeur, alors nous aurons la fraction molaire de B dans la phase de vapeur (x_B^V). De même, le point C, sur la ligne droite du liquide, nous donnera la fraction molaire de B dans la phase liquide (x_B^L).

La règle de levier est basée précisément sur la ligne de liaison et les distances entre x_B^L, X_B et x_B^V.

Déduction mathématique

La fraction molaire globale de B est égale à:

X_B = n_B / (n^L + n^V)

Où n_B Ce sont les moles totaux de B à la fois en phase liquide et vapeur, et n^L et n^V sont les moles respectives pour ces phases. Clairière n_B nous aurons:

n_B = X_Bn^L + X_Bn^V (1)

D'un autre côté, n_B Il est également égal à:

n_B = n_B^L + n_B^V

= X_B^Ln^L + X_B^Vn^V  (2)

Désormais, égalise les équations (1) et (2) nous donnera:

X_Bn^L + X_Bn^V = X_B^Ln^L + X_B^Vn^V

Et réorganiser:

n^L(X_B - X_B^L) = n^V(X_B^V - X_B) (3)

n^L(C-d) = n^V(DE)

Ces deux dernières expressions mathématiques sont la règle du levier. Notez que x_B - X_B^L C'est la distance entre les points C et D; et x_B^V - X_B, C'est la distance entre les points D-E: les deux moitiés de la ligne de liaison (bras de levier).

Cette équation est très similaire à celle décrivant l'équilibre des masses sur un rocker avec Fulcro:

m₁l₁ = m₂l₂

Ainsi, la règle de levier nous permettra de calculer le total des grains n^L et n^V à condition que les moles totales du mélange soient connues, n_T (n_T = n^L + n^V).

Deuxième forme

L'expression précédente pour la règle de levier sert à calculer les quantités (masses, taupes, etc.) des phases en équilibre. Cependant, la version la plus connue de la règle du levier nous permet de calculer les fractions ou les pourcentages de chaque phase, ne prenant que les distances entre x_B, X_B^L et x_B^V.

Considérez le même système ci-dessus, ayant une autre forme de la règle du levier:

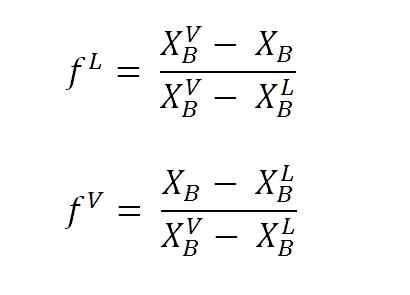Équations pour calculer les fractions liquides et vapeur à l'aide des bras de levier. Source: Gabriel Bolívar.

Où F ^L et F ^VCe sont des fractions molaires (ou pour pourcentage, selon le graphique) des phases liquide et vapeur, respectivement. Notez que, évidemment, F ^L et F ^V Ils n'ont pas d'unités; tandis que n^L et n^V Oui, ils ont des unités (grammes, grammes, etc.).

Peut vous servir: chaleur de réaction

Exemples

Méthode 1

Dans un conteneur 28 moles de b et 12 moles de a sont mélangés. Déterminez les quantités et les fractions molaires pour les phases formées.

Nous calculons x_B:

X_B = (28 moles B) / (28 moles B + 12 moles A)

= 0.7

Cette valeur correspond à x_B du diagramme supérieur. Les interceptions nous donneront approximativement les valeurs suivantes pour x_B^L et x_B^V:

X_B^L = 0.41

X_B^V = 0.94

Avec la règle du levier:

n^L(X_B - X_B^L) = n^V(X_B^V - X_B)

Et sachant que n_T = n^L + n^V, et que n_T = 40 moles, alors nous nettoyons n^L soit n^V Selon l'autre:

n^L(X_B - X_B^L) = (40 moles - n^L) (X_B^V - X_B)

Réarrangement et nettoyage n^L nous aurons:

n^L = (40 moles) (x_B^V - X_B) / (X_B^V - X_B^L)

Cette expression ne se souvient-elle pas celle de F ^L? Maintenant en remplacement, nous aurons:

n^L = (40 moles) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 moles en phase liquide

Nous pouvons calculer n^V De deux façons:

n^V = n^L(X_B - X_B^L) / (X_B^V - X_B)

soit

n^V = 40 moles - 18.11 moles

= 21.89 moles en phase de vapeur

Méthode 2

Et si nous calculons d'abord F ^L et F ^V?

F ^L = (X_B^V - X_B) / (X_B^V - X_B^L)

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 ou 45.28%

C'est-à-dire 45.2% des taupes sont en phase liquide, étant cette quantité égale à:

n^L = F ^Ln_T

= (0.4528) (40 moles)

= 18.11 moles

ET F ^V Nous pouvons le calculer également de deux manières:

F ^V = 1 - F ^L

soit

F ^V = (X_B - X_B^L) / (X_B^V - X_B^L)

Étant sa valeur:

F ^V = 0.5472 ou 54.72%

Et par conséquent, n^V Il sera égal à:

n^V = F ^Vn_T

= (0.5472) (40 moles)

= 21.89 moles

Notez que l'application des deux formes de la règle de levier comme méthodes de calcul alternatives, les mêmes résultats peuvent être atteints. La méthode 2 semble plus directe et simple; Mais s'il est observé avec soin, une fois la compensation résolue n^L soit n^V, On verra que les deux méthodes sont en fait tout aussi faciles.

Exercices résolus

Ensuite, deux autres exercices seront résolus, où maintenant les systèmes considérés impliqueront un liquide solide et non-liquide-vapeur. De plus, les diagrammes sont graphiques par rapport à la température du système et non à leur pression.

Exercice 1

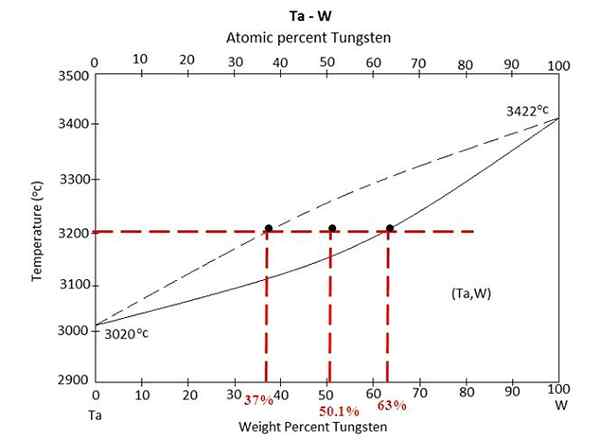Diagramme de phase pour un alliage entre Tantalo et Tungstène. Source: Materimeddia, CC BY-SA 4.0, via Wikimedia Commons

Nous avons le diagramme de phase au-dessus d'un alliage entre Tantalo et Tungsten, Ta-W. Sur l'axe X, les pourcentages de masse mondiaux du tungstène, W% (m / m) sont représentés.

Dans la région d'équilibre liquide (TA + W) et solide (alliage), il y a un mélange à 3200 ºC. Déterminez les masses de chaque phase en supposant que 100 grammes d'alliage ont été chauffés.

Il peut vous servir: métaux, non-métaux et métalloïdes

Procédure

Cette fois, l'exercice sera résolu en utilisant la deuxième forme de la règle du levier. La ligne syndicale nous dit que: dans la phase solide, nous avons 63% du tungstène, tandis que dans la phase liquide, nous avons 37% de tungstène. En effet.

Donc nous avons:

W%^S ou w_S= 63%

W%^L ou w_L= 37%

Et aussi:

W₀ = 50.1%

Nous appliquons la règle du levier à F ^L:

F ^L = (63% - 50.1%) / (63% - 37%)

= 0.4961 ou 49.61%

Notez que la distance correspondant à la phase liquide est le bras de levier près de la phase solide, le côté opposé du point moyen.

La masse de la phase liquide est donc:

(0.4961) (100 grammes) = 49.61 grammes fondus

Et la phase solide sera égale à:

100 grammes - 49.61 grammes = 50.39 grammes d'alliage riche en tungstène

Exercice 2

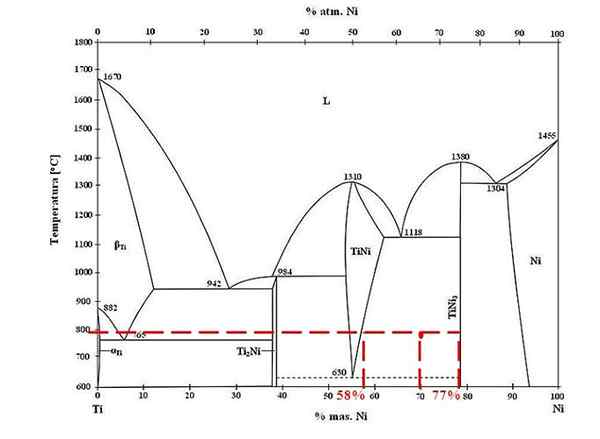Diagramme de phase pour les alliages de nickel en titane. Source: Doomgiver, CC BY-SA 3.0, via Wikimedia Commons

Pour le titane et l'alliage de nickel à 800 ºC, et avec 70% de nickel, déterminez la quantité de Tini et Tini₃ Ils sont présents.

Procédure

Cette fois, ils ne demandent que les fractions de masse de chaque phase. Le point rouge est situé dans la région d'équilibre entre les phases Tini et Tini₃, dont les courbes sont là où il joue la ligne d'union qui s'écoule vers les valeurs de 58% ou pour la phase Tini, et 77% ou pour la phase Tini₃.

Notez que le point rouge est plus proche de la phase Tini₃ celui de la phase Tini. Cela signifie qu'il doit y avoir plus de tini₃ ce tini; Et donc, la distance ou le bras de levier correspondant à Tini₃ Ce doit être le plus long, le contraire (70% -58%).

Sachant cela, nous procédons à calculer F ^Tini3:

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 ou 63.16%

En effet, 63.16% de l'alliage correspond à la phase Tini₃. Pendant ce temps, la phase Tini correspond à:

1 = F ^Tini3 + F ^Inonique

F ^Inonique = 1 - F ^Tini3

= 0.3684 ou 36.84%

En conclusion aux exercices soulevés, nous pouvons dire que la règle du levier est très utile pour déterminer les fractions de chaque phase en équilibre pour un système à deux composantes.

Les références

1. Walter J. Moore. (1963). Chimie physique. Dans la cinétique chimique. Quatrième édition, Longmans.
2. L'Iran. Levine. (2009). Principes de la physicochimie. Sixième édition. Mc Graw Hill.
3. Wikipédia. (2020). Règle de levier. Récupéré de: dans.Wikipédia.org
4. Michael Adewumi. (18 mai 2020). La règle du levier. Récupéré de: Eng.Bibliothèque.org
5. Adam Warren. (1997). Diagrammes de phase: les lignes d'attache et la règle du levier. Récupéré de: Southampton.CA.ROYAUME-UNI
6. Université de Cambridge. (2020). La règle du levier. Récupéré de: Doitpoms.CA.ROYAUME-UNI