Règle de droite

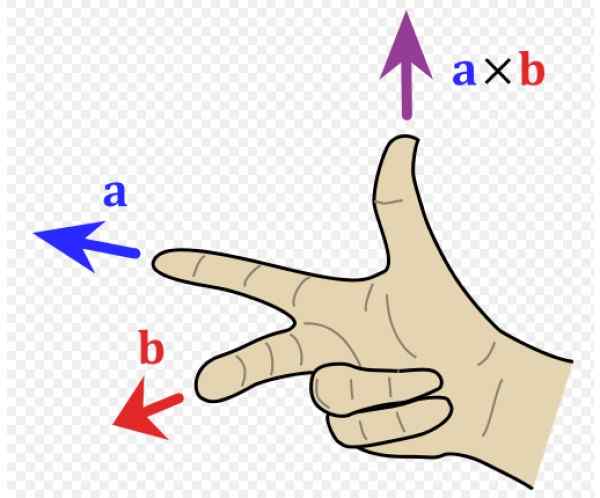
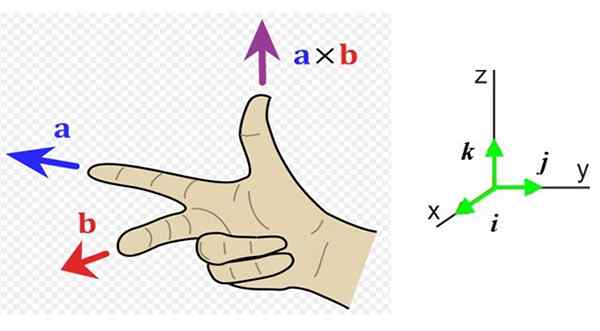Figure 1. Règle de droite. Source: Wikimedia Commons. ACDX [CC BY-S (http: // CreatiVecommons.Org / licences / by-sa / 3.0 /]].

Quelle est la règle de droite?

La règle de droite Il s'agit d'une ressource mnémonique pour établir la direction et la direction du vecteur résultant d'un produit vectoriel ou d'un produit transversal. Il est largement utilisé en physique, car il existe des amplitudes vectorielles importantes qui sont le résultat d'un produit vectoriel. C'est le cas du couple, de la force magnétique, du moment angulaire et du moment magnétique, par exemple.

Être deux vecteurs génériques pour et b dont le produit croisé est pour X b. Le module d'un tel vecteur est:

pour X b = pour.b.Sin α

Où α est l'angle minimum entre pour et b, Tandis que A et B représentent leurs modules. Pour distinguer les vecteurs de leurs modules, des lettres audacieuses sont utilisées.

Maintenant, nous devons connaître la direction et la signification de ce vecteur, il est donc pratique d'avoir un système de référence avec les trois directions de l'espace (figure 1 à droite). Les vecteurs unitaires Toi, J et k Ils pointent respectivement au lecteur (hors de la page), à ​​droite et vers le haut.

Dans l'exemple de la figure 1 à gauche, le vecteur pour se dirige vers la gauche (adresse et négatif et index de la main droite) et le vecteur b va au lecteur (adresse X Positif, doigt majeur de la main droite).

Le vecteur résultant pour X b a la direction du pouce, dans la direction z positif.

Deuxième règle de la main droite

Cette règle est beaucoup utilisée lorsqu'il y a des amplitudes dont la direction et le sens tournent, comme le champ magnétique B produit par un fil mince et rectiligne qui transporte un courant.

En tal caso las líneas de campo magnético son circunferencias concéntricas con el alambre, y el sentido del giro se obtiene con esta regla de la siguiente forma: el pulgar derecho señala la dirección de la corriente y los cuatro dedos restantes se curvan en la dirección del Campagne. Nous illustrons le concept de la figure 2.

Peut vous servir: chocs élastiques: dans une dimension, des cas spéciaux, des exercices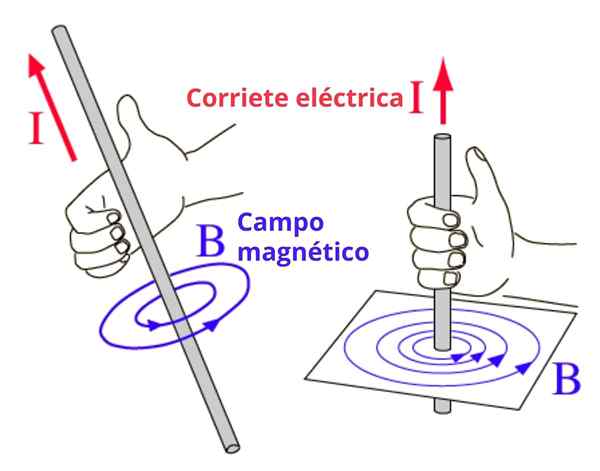Figure 2. Règle de droite pour déterminer la signification de la circulation du champ magnétique

Règle alternative de la main droite

La figure suivante montre une forme alternative de la règle de droite. Les vecteurs qui apparaissent dans les Lumières sont:

• La vitesse V d'une charge ponctuelle qui.
• Le champ magnétique B Dans lequel la charge se déplace.
• F_B La force que le champ magnétique exerce sur la charge.

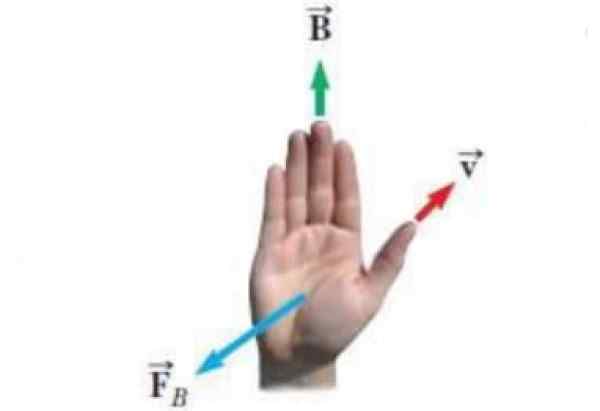figure 3. Règle alternative de la main droite. Source: Wikimedia Commons. ExpertiCuis [cc by-sa (https: // createCommons.Org / licences / by-sa / 4.0)]

L'équation de la force magnétique est F_B = qV X B et la règle de la main droite pour connaître la direction et le sens de F_B Cela s'applique comme ceci: les points du pouce selon V, les quatre doigts restants sont placés selon le champ B. Ensuite F_B C'est un vecteur qui sort de la paume de la main, perpendiculaire à lui, comme s'il poussait la charge.

Noter que F_B pointerait dans la direction opposée si la charge était négative, car le produit vectoriel n'est pas commutatif. En fait:

pour X B = - b X pour

Applications

La règle de la main droite peut être appliquée à diverses amplitudes physiques, en savons certains d'entre eux:

Vitesse et accélération angulaires

À la fois la vitesse angulaire Ω Comme l'accélération angulaire α Ce sont des vecteurs. Si un objet tourne autour d'un axe fixe, c'est possible la vitesse angulaire Ω.

Pour sa part, l'accélération angulaire α aura la même adresse que Ω, Mais sa signification dépend de si Ω augmente ou diminue son ampleur au fil du temps. Dans le premier cas, les deux ont la même direction et le même sens, mais dans la seconde, ils auront des sens opposés.

Peut vous servir: Law Watt: Qu'est-ce que les exemples, les applications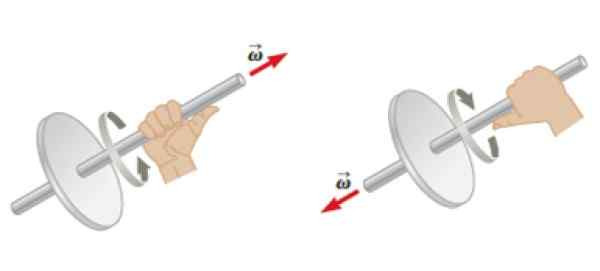Figure 4. La règle de la main droite s'appliquait à un objet en rotation pour déterminer la direction et la direction de la vitesse angulaire. Source: Serow, R. Physique.

Le moment angulaire

Le vecteur angulaire L_SOIT d'une particule qui tourne autour d'un certain axe ou est définie comme le produit vectoriel de son vecteur de position instantanée r  et la quantité de mouvement linéaire p:

L = r X p

La règle de main droite est appliquée de cette manière: l'index est placé dans la même direction et la même direction de r, Le majeur dans le p, les deux sur un plan horizontal, comme sur la figure. Automatiquement, le pouce s'étend verticalement vers le haut en pointant la direction et la direction du moment angulaire L_SOIT.

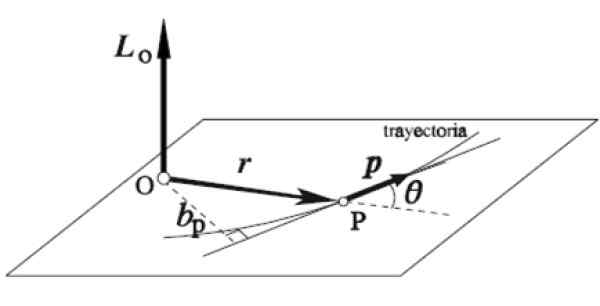Figure 5. Le vecteur angulaire. Source: Wikimedia Commons.

Exercices

Exercice 1

Le spin de la figure 6 va rapidement avec la vitesse angulaire Ω et son axe de symétrie brisé plus lentement autour de l'axe vertical z. Ce mouvement est appelé précession. Décrire les forces qui agissent sur le rotation et l'effet qu'ils produisent.

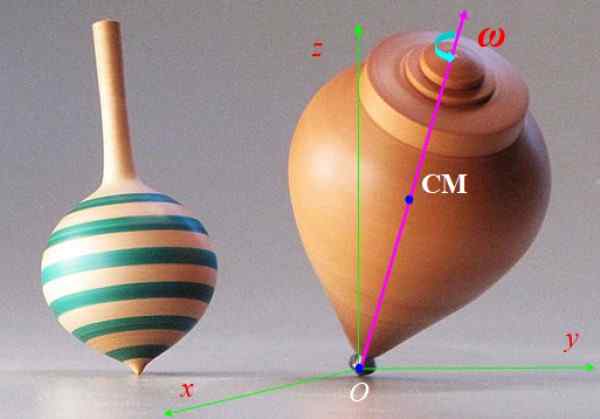Figure 6. Rotation. Source: Wikimedia Commons.

Solution

Les forces agissant sur le spin sont normales N, appliqué au point de support avec le sol ou plus le poids mg, appliqué au centre de la masse cm, avec g Le vecteur d'accélération de gravité, dirigé verticalement en bas (voir figure 7).

Les deux forces sont équilibrées, donc le spin ne bouge pas. Cependant, le poids produit un couple ou un couple τ Net sur le point ou, donné par:

τ_SOIT = r_SOIT X F, avec F = Mg.

Comme r et Mg Ils sont toujours dans l'avion à mesure que le rotation tourne, selon la règle de la main droite le couple τ_SOIT Il est toujours situé dans l'avion Xy, perpendiculaire à la fois un r comme g.

Noter que N ne produit pas de couple par rapport à O, car son vecteur r Concernant ou est nul. Ce couple produit un changement dans le moment angulaire qui provoque la précession de la rotation autour de l'axe z.

Peut vous servir: équilibre thermodynamique: classes et applications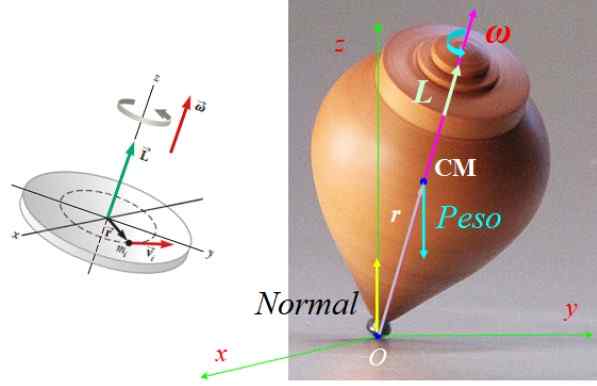Figure 7. Forces agissant sur le spin et son vecteur de moment angulaire. Source de la figure de gauche: Serow, R. Physique pour la science et l'ingénierie.

Exercice 2

Soulignez la direction et la direction du vecteur de moment angulaire L de la Trump de la figure 6.

Solution

Tout point de la rotation a la masse m_Toi, vitesse V_Toi et vecteur de position r_Toi, Quand il tourne autour de l'axe z. Le moment angulaire L_Toi de cette particule est:

L_Toi = r_Toi X p_Toi = r_Toi x m_ToiV_Toi

Étant donné que r_Toi et V_Toi Ils sont perpendiculaires, l'ampleur de L est:

L_Toi = m_Toir_ToiV_Toi

La vitesse linéaire V est lié à la vitesse angulaire Ω à travers:

V_Toi = r_ToiΩ

Donc:

L_Toi = m_Toir_Toi (r_ToiΩ) = m_Toir_Toi²Ω

Le moment angulaire total du tripo l est la somme du moment angulaire de chaque particule:

L = (∑m_Toir_Toi² ) Ω

∑ m_Toir_Toi²  C'est le moment de l'inertie I du spin, alors:

L= IΩ

Donc L et Ω Ils ont la même direction et le même sens, comme le montre la figure 7.