Racine carrée de 3 (solution facile et explication)

La racine carrée de 3 est de 1,73205080756887.

Il peut être exprimé:

√3 = 1,73205080756887

Savoir ce qu'est le Racine à 3 carrés, Il est important de connaître la définition de la racine carrée d'un nombre. Étant donné un nombre positif "A", la racine carrée de "A", désignée par √a, est un nombre positif "B" tel que lorsque "B" est multiplié par lui, le résultat est "A".

La définition mathématique indique: √a = b oui, et seulement si, b² = b * b = a. Par conséquent, pour savoir quelle est la racine carrée de 3, c'est-à-dire la valeur de √3, un nombre «b» doit être trouvé que b² = b * b = √3.

De plus, √3 est un nombre irrationnel, qui se compose d'une quantité infinie non périodique de décimales. Pour cette raison, il est difficile de calculer la racine carrée de 3 manuellement.

Racine à 3 carrés

Si une calculatrice est utilisée, on peut voir que la racine carrée de 3 est de 1,73205080756887…

Maintenant, vous pouvez essayer manuellement de se rapprocher de ce numéro comme suit:

-1 * 1 = 1 et 2 * 2 = 4, cela dit que la racine carrée de 3 est un nombre entre 1 et 2.

-1,7 * 1,7 = 2,89 et 1,8 * 1,8 = 3,24, par conséquent, la première chiffre décimal est 7.

-1,73 * 1,73 = 2,99 et 1,74 * 1,74 = 3,02, donc la deuxième chiffre décimal est 3.

-1 732 * 1 732 = 2,99 et 1 733 * 1 733 = 3,003, par conséquent, la troisième décimale est 2.

Et ainsi de suite vous pouvez continuer. Ceci est un moyen manuel de calculer la racine carrée de 3.

Il existe également d'autres techniques beaucoup plus avancées, comme la méthode Newton-Raphson, qui est une méthode numérique pour calculer les approximations.

Où pouvons-nous trouver le nombre √3?

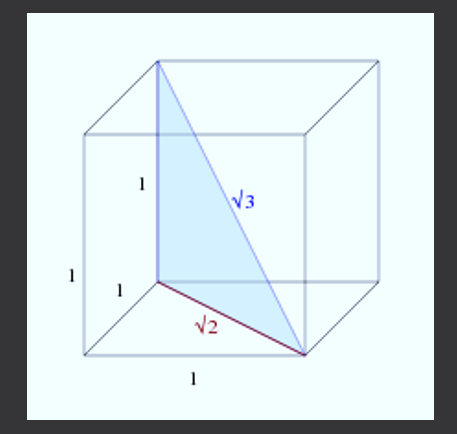
En raison du nombre compliqué, on pourrait penser qu'il n'apparaît pas dans les objets du quotidien mais c'est faux. Si vous avez un cube (boîte carrée), de sorte que la longueur de ses côtés est 1, alors les diagonales du cube auront une mesure de √3.

Pour vérifier cela, le théorème de Pythagore est utilisé qui dit: donner.

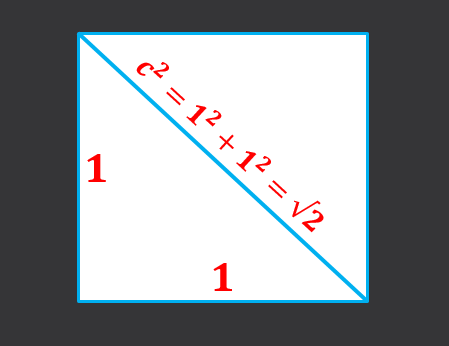
Ayant un côté du côté 1, vous devez diagonale du carré de sa base est égal à la somme des carrés des catégories, c'est-à-dire C² = 1² + 1² = 2, par conséquent, la diagonale de la mesure de base √2.

Maintenant, pour calculer la diagonale du cube, vous pouvez voir la figure suivante.

Le nouveau triangle rectangle a des jambes de longueurs 1 et √2, par conséquent, lors de l'utilisation du théorème de Pythagore pour calculer la longueur de sa diagonale, il est obtenu: c² = 1² + (√2) ² = 1 + 2 = 3, c'est dire , C = √3.

Ainsi, la longueur de la diagonale d'un seau latéral 1 est égale à √3.

√3 Un nombre irrationnel

Au début, il a été dit que √3 est un nombre irrationnel. Pour vérifier cela, il est supposé par l'absurdité qui est un nombre rationnel, qu'il y a deux nombres "A" et "B", des cousins ​​relatifs, tels que A / B = √3.

Lorsque la dernière égalité et claire «a²», l'équation suivante est obtenue: a² = 3 * b². Cela dit que "a²" est un multiple de 3, ce qui conclut que "A" est un multiple de 3.

Étant "un" multiple de 3, il y a un entier "k" tel que a = 3 * k. Par conséquent, en remplaçant dans la deuxième équation, il est obtenu: (3 * k) ² = 9 * k² = 3 * b², qui est le même que b² = 3 * k².

Comme précédemment, cette dernière égalité conduit à la conclusion que "B" est un multiple de 3.

En conclusion, "A" et "B" sont tous deux des multiples de 3, ce qui est une contradiction, car au début, il a été supposé qu'ils étaient des cousins ​​relatifs.

Par conséquent, √3 est un nombre irrationnel.