Test de Tukey dans ce qui est, maître, exercice résolu

La Test de Tukey Il s'agit d'une méthode qui vise à comparer les moyennes individuelles d'une analyse de la variance de plusieurs échantillons sous.

Le test, présenté en 1949 par John.W. Tukey, permet de discerner si les résultats obtenus sont significativement différents ou non. Il est également connu comme le Test de différence de Tukey honnêtement significative (Test de HSD de Tukey pour ses sigles en anglais).

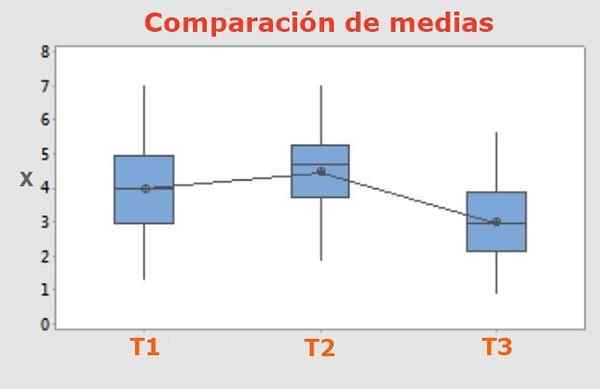
Figure 1. Le test Tukey permet de discerner si les différences de résultat entre trois ou plusieurs traitements différents appliqués à trois groupes ou plus de caractéristiques égales, ont des valeurs moyennes significatives et honnêtement différentes.

Dans des expériences où il compare entre trois ou plusieurs traitements différents appliqués au même nombre d'échantillons, il est nécessaire de discerner si les résultats sont significativement différents ou non.

On dit qu'une expérience est équilibrée lorsque la taille de tous les échantillons statistiques est la même dans chaque traitement. Lorsque la taille de l'échantillonnage est différente pour chaque traitement, il y a alors une expérience non équilibrée.

Parfois, il ne suffit pas d'une analyse de variance (ANOVA) de savoir si dans la comparaison de différents traitements (ou expériences) appliqués à plusieurs échantillons, ils répondent à l'hypothèse nulle (HO: "Tous les traitements sont les mêmes") ou au contraire rencontre l'hypothèse alternative (HA: "Au moins l'un des traitements est différent").

Le test Tukey n'est pas unique, il existe de nombreuses autres preuves pour comparer les moyens d'échantillon, mais c'est l'un des plus connus et appliqués.

[TOC]

Comparateur et table de Tukey

Dans l'application de ce test, une valeur est calculée W appelé le Comparateur de Tukey dont la définition est la suivante:

W = q √ (mse / r)

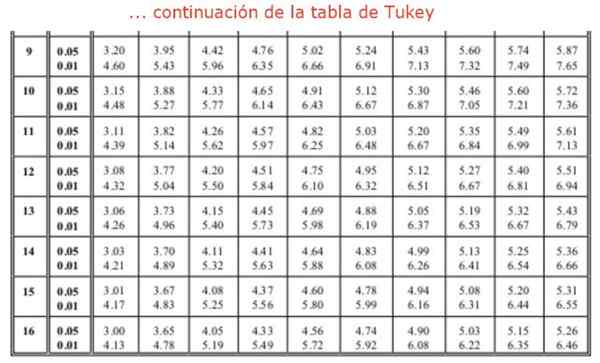
Où le facteur q Il est obtenu à partir d'une table (table Tukey), qui se compose de rangs de valeurs q Pour un nombre différent de traitements ou d'expériences. Les colonnes indiquent la valeur du facteur q Pour différents degrés de liberté. Normalement, les tables disponibles ont des moyens relatifs de 0.05 et 0.01.

Peut vous servir: en attente de ligne: formule et équations, représentation, exemples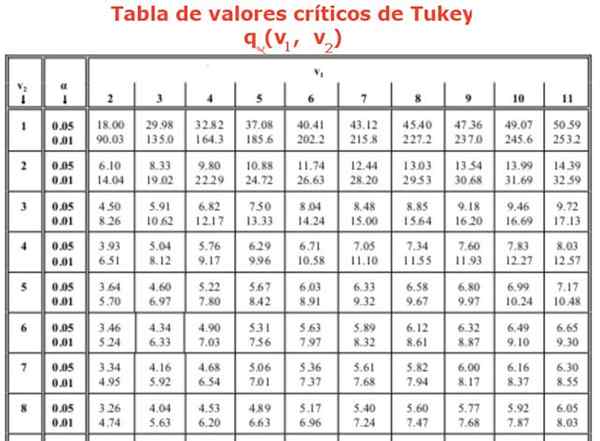

Dans cette formule, dans la racine carrée, le facteur MSE apparaît (carré moyen de l'erreur) divisé par R, ce qui indique le nombre de répétitions. Le MSE est un nombre qui est normalement obtenu à partir d'une analyse des variances (ANOVA).

Lorsque la différence entre deux valeurs moyennes dépasse la valeur W (Comparateur Tukey), alors il est conclu que ce sont des moyennes différentes, mais si la différence est inférieure au nombre de Tukey, alors ce sont deux échantillons avec une valeur moyenne statistiquement identique.

Le nombre W est également connu sous le nom de nombre HSD (différence honnêtement significative).

Ce seul numéro de comparateur peut être appliqué si le nombre d'échantillons appliqués pour le test de chaque traitement est le même dans chacun d'eux.

Expériences déséquilibrées

Lorsque pour une raison quelconque, la taille des échantillons est différente dans chaque traitement à comparer, la procédure décrite ci-dessus diffère légèrement et est connue sous le nom Test de Tukey-Kramer.

Maintenant, un nombre est obtenu W Comparateur pour chaque paire de traitements I, J:

w (i, j) = q √ (½ mse / (ri + rj))

Dans cette formule, le facteur obtenu à partir de la table Tukey. Ledit facteur qui dépend du nombre de traitements et des degrés de liberté d'erreur. r_Toi C'est le nombre de répétitions dans le traitement I, tandis que r_J C'est le nombre de répétitions dans le traitement J.

Exemple de cas

Un éleveur de lapins veut faire une étude statistique fiable qui indique que les quatre marques alimentaires de lapin sont les plus efficaces. Pour l'étude, il forme quatre groupes avec des lapins de six mois et demi qui jusqu'à ce temps avaient les mêmes conditions alimentaires.

De l'expérience au premier groupe, il est appelé A1 car il se nourrira de la nourriture de la marque 1, de même avec le groupe A2, A3 et A4. Une table est faite où le gain de poids (en livres) de chaque spécimen après un mois de nourriture avec les différentes marques alimentaires est enregistré, obtenant les résultats suivants: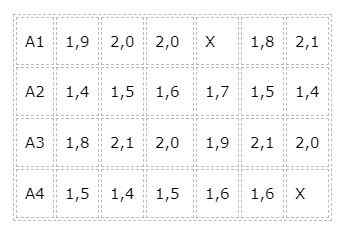Bien qu'il ait commencé par une expérience équilibrée, en ce sens que le nombre de lapins auxquels le traitement serait appliqué était le même, l'expérience ne pouvait pas être terminée de cette manière.

Peut vous servir: homotecia négative

Les raisons étaient que, dans les décès A1 et A4, sur les groupes, en raison de causes non attribuables à la nourriture, car l'un des lapins a été coupé par un insecte et dans l'autre cas, le décès était sûrement la cause d'un défaut congénital. Pour que les groupes soient déséquilibrés, puis il est nécessaire d'appliquer le test Tukey-Kramer.

Exercice résolu

Afin de ne pas trop étendre les calculs, un cas d'expérience équilibrée sera considéré comme un exercice résolu. Ce qui suit sera considéré comme des données:

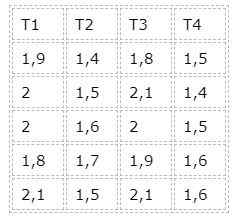
Dans ce cas, il existe quatre groupes correspondant à quatre traitements différents. Cependant, nous observons que tous les groupes ont le même nombre de données, il s'agit donc d'un cas équilibré.

Pour effectuer l'analyse ANOVA, l'outil qui est incorporé dans la feuille de calcul de Libreoffice. Autres feuilles de calcul telles que Exceller Ils ont cet outil pour l'analyse des données incorporée. Vous trouverez ci-dessous un tableau récapitulatif qui a résulté après l'analyse de la variance (ANOVA):

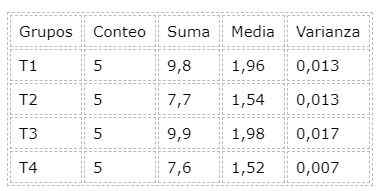
D'après l'analyse de la variance, il y a aussi la valeur p, qui par exemple est 2,24e-6 bien en dessous de 0.05 du niveau de signification, qui conduit directement à rejeter l'hypothèse nulle: tous les traitements sont égaux. 

Autrement dit, parmi les traitements, certains ont des valeurs moyennes différentes, mais vous devez savoir quels sont les points de vue significatifs et honnêtement différents du point de vue statistique en utilisant le test de Tukey.

Pour trouver le nombre w ou comme le nombre HSD est également connu, nous avons besoin du carré moyen de l'erreur MSE. D'après l'analyse ANOVA, il est obtenu que la somme des carrés au sein des groupes est SS = 0,2; Et le nombre de degrés de liberté au sein des groupes est df = 16 avec ces données que nous pouvons trouver MSE:

Peut vous servir: Papomudas

Mse = ss / df = 0,2 / 16 = 0,0125

Il est également nécessaire pour trouver le facteur q de Tukey, en utilisant la table. Il est recherché dans la colonne 4 qui correspond aux 4 groupes ou traitements à comparer et la ligne 16, car l'analyse ANOVA a montré 16 degrés de liberté au sein des groupes. Cela nous amène à une valeur de q égal à: Q = 4,33 correspondant à 0,05 signification ou fiabilité à 95%. Enfin, la valeur de la "différence honnêtement significative" est trouvée:

W = hsd = Q √ (MSE / R) = 4,33 √ (0,0125 / 5) = 0,2165

Pour savoir quels sont les groupes ou traitements honnêtement différents, vous devez connaître les moyennes de chaque traitement:

Il est également nécessaire de connaître les différences entre les valeurs moyennes des paires de traitements, qui sont montrés dans le tableau suivant:

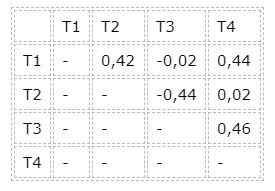Les groupes T3 et T1, ainsi que les groupes T2 et T4, sont de résultats identiques. Ainsi, les groupes honnêtement différents sont les groupes T1 et T2 ou T3 et T4, car la différence dans leurs valeurs moyennes dépasse la valeur HSM du test Tukey.

Il est conclu que les meilleurs traitements, en termes de maximisation du résultat, sont le T1 ou le T3, qui sont indifférents du point de vue statistique. Pour choisir entre T1 et T3, d'autres facteurs extérieurs à l'analyse présentés ici doivent être recherchés. Par exemple, prix, disponibilité, etc.

Les références

1. Cochran William et Cox Gertrude. 1974. Conceptions expérimentales. Trille. Mexique. Troisième réimpression. 661p.
2. Snedecor, G.W. Et cochran, w.g. 1980. Méthodes statistiques. Septième Ed. Iowa, Iowa State University Press. 507p.
3. Acier, R.g.D. Et Torrie, J.H. 1980. Principes et procédures des statistiques: une approche biométrique (2e éd.). McGraw-Hill, New York. 629p.
4. Tukey, J. W. 1949. Comparaison individuelle des moyens dans l'analyse de la variance. Biométrie, 5: 99-114.
5. Wikipédia. Test de Tukey. Récupéré de: dans.Wikipédia.com