Formules de coefficient de détermination, calcul, interprétation, exemples

Il Coefficient de détermination C'est un nombre entre 0 et 1 qui représente la fraction des points (x, y) qui suivent la ligne de réglage par régression d'un ensemble de données avec deux variables.

Il est également connu sous le nom bonté d'ajustement et est indiqué par r². Pour le calculer, le quotient est pris entre la variance des données ŷi estimées par le modèle de régression et la variance des données YI correspondant à chaque xi des données.

R² = Sŷ / sy

Figure 1. Coefficient de corrélation pour quatre paires de données. Source: F. Zapata.

Si 100% des données sont sur la ligne de fonction de régression, le coefficient de détermination sera 1.

Au contraire, si pour un ensemble de données et une certaine fonction d'ajustement, le coefficient R² Il s'avère être égal à 0.5, alors on peut dire que l'ajustement est satisfaisant ou bon à 50%. 

De même, lorsque le modèle de régression jette les valeurs de R² Moins de 0.5, cela indique que la fonction d'ajustement choisie ne s'adapte pas de manière satisfaisante aux données, donc nécessaire pour rechercher une autre fonction d'ajustement.

Et quand covariance ou la Coefficient de corrélation Il tend à zéro, puis les variables x et y des données ne sont pas liées, et donc r² tend également à zéro.

[TOC]

Comment calculer le coefficient de détermination?

Dans la section précédente, il a été dit que le coefficient de détermination est calculé en trouvant le quotient entre les variances:

-Estimé par la fonction de régression de la variable et 

-La variable yi correspondant à chacune des variables Xi. 

Sous forme mathématique, il reste comme ceci:

R² = Sŷ / sy

De cette formule, il s'ensuit que r² représente la proportion de variance expliquée par le modèle de régression. Alternativement, R peut être calculé² Grâce à la formule suivante, totalement équivalent à la précédente:

R² = 1 - (sε / sy)

Où sε représente la variance des déchets εi = ŷi - yi, tandis que sy est la variance de l'ensemble de données des données des données. Pour déterminer ŷi la fonction de régression est appliquée, ce qui signifie affirmer que ŷi = f (xi).

Il peut vous servir: une fraction équivalente à 3/5 (solution et explication)

La variance de l'ensemble de données YI, avec I de 1 à n est calculée de cette manière:

Sy = [σ (yi -)² ) / (N-1)]

Puis procéder de manière similaire pour Sŷ ou pour Sε.

Cas illustratif

En montrant le détail de la façon dont le calcul du Coefficient de détermination Nous prendrons l'ensemble suivant de quatre paires de données: 

(X, y): (1, 1); (23); (3, 6) et (4, 7).

Un ajustement de régression linéaire est proposé pour cet ensemble de données obtenu par la méthode des minimums carrés:

f (x) = 2.1 x - 1 

En appliquant cette fonction d'ajustement, les pairs sont obtenus:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) et (4, 7.4).

Ensuite, nous calculons la moyenne arithmétique pour x et y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Variance sy

Sy = [(1 - 4.25)² + (3. 4.25)² + (6 - 4.25)² +.. ... .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Variance sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +.. ... .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Coefficient de détermination r²

R² = Sŷ / sy = 7.35/7.58 = 0.97

Interprétation

Le coefficient de détermination du cas illustratif considéré dans le segment précédent s'est avéré être 0.98. C'est-à-dire que le réglage linéaire à travers la fonction:

 f (x) = 2.1x - 1

Il est fiable à 98% d'expliquer les données avec lesquelles elle a été obtenue via la méthode carrée minimale. 

En plus du coefficient de détermination, il y a le Coefficient de corrélation linéaire ou également connu sous le nom de coefficient de Pearson. Ce coefficient, désigné comme r, Il est calculé par la relation suivante:

R = sxy / (sx sy)

Ici, le numérateur représente la covariance entre les variables x et y, tandis que le dénominateur est le produit de l'écart type pour la variable x et l'écart type pour la variable et.

Le coefficient de Pearson peut prendre des valeurs entre -1 et +1. Lorsque ce coefficient tend à +1, il y a une corrélation linéaire directe entre x et y. Si à la place, il a tendance à -1, il y a une corrélation linéaire mais quand x se développe et diminue. Enfin, il est proche de 0, il n'y a pas de corrélation entre les deux variables.

Peut vous servir: données groupées: exemples et exercice résolus

Il convient de noter que le coefficient de détermination coïncide avec le carré du coefficient de Pearson, uniquement lorsque le premier a été calculé sur la base d'un ajustement linéaire, mais cette égalité n'est pas valable pour d'autres ajustements non linéaires.

Exemples

- Exemple 1

Un groupe d'élèves du secondaire a l'intention de déterminer une loi empirique pour la période d'un pendule en fonction de sa longueur. Pour atteindre cet objectif, ils effectuent une série de mesures dans lesquelles ils mesurent le temps d'une oscillation pendule pour différentes longueurs obtenant les valeurs suivantes:

Longueur (m)	Période (s)
0.1	0.6
0.4	1.31
0.7	1.78
1	1.93
1.3	2.19
1.6	2.66
1.9	2.77
3	3.62

Il est invité à faire un graphique de dispersion des données et à effectuer un ajustement linéaire par régression. De plus, montrez l'équation de régression et son coefficient de détermination.

Solution

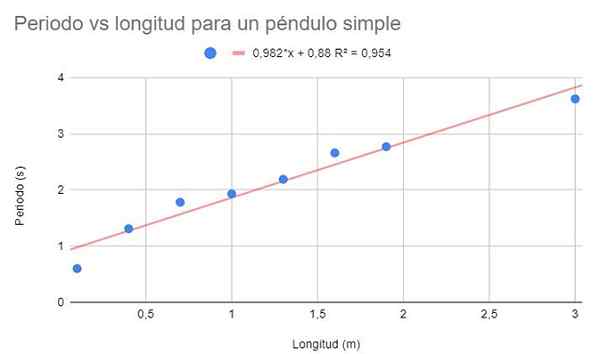Figure 2. Solution graphique de l'exercice 1. Source: F. Zapata.

Un coefficient de détermination assez élevé (95%) peut être observé, il est donc possible de penser que le réglage linéaire est optimal. Cependant, si les points sont observés ensemble, il semble qu'ils aient tendance à se courber. Ce détail n'est pas envisagé dans le modèle linéaire.

- Exemple 2

Pour les mêmes données de l'exemple 1, faites un tableau de dispersion des données. À cette occasion, contrairement à l'exemple 1, il est invité à effectuer un ajustement de régression à travers une fonction potentielle.

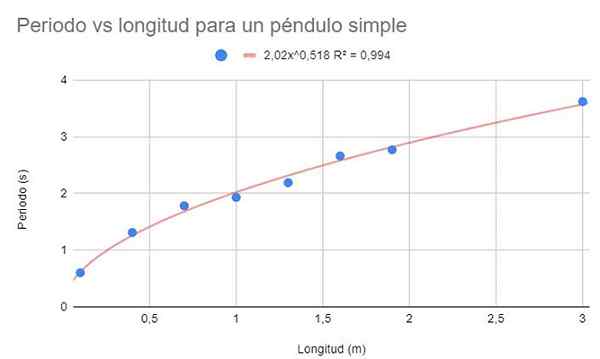figure 3. Solution graphique de l'exercice 2. Source: F. Zapata.

Affichent également la fonction d'ajustement et son coefficient de détermination R².

Solution

La fonction potentielle est de la forme f (x) = hache^B, où a et b sont constants qui sont déterminés par la méthode carrée minimale.

La figure précédente montre la fonction potentielle et ses paramètres, ainsi que le coefficient de détermination avec une valeur très élevée de 99%. Notez que les données suivent la courbure de la ligne de tendance.

Peut vous servir: principe additif

- Exemple 3

Avec les mêmes données d'exemples 1 et d'exemple 2, effectuez un ajustement polynomial de deuxième degré. Afficher le graphique, le polynôme de réglage et le coefficient de détermination r² correspondant.

Solution

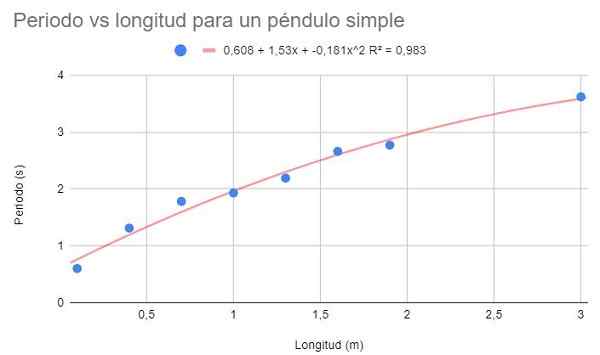Figure 4. Exercice graphique 3 graphique. Source: F. Zapata.

Avec le réglage polynomial au deuxième degré, une ligne de tendance peut être vue qui s'adapte bien à la courbure des données. De même, le coefficient de détermination est au-dessus du réglage linéaire et en dessous du réglage potentiel.

Comparaison de réglage

Des trois ajustements indiqués, celui avec un coefficient de détermination plus élevé est le réglage potentiel (exemple 2).

L'ajustement potentiel coïncide avec la théorie physique du pendule, qui, comme on le sait, établit que la période d'un pendule est proportionnelle à la racine carrée de sa longueur, étant la constante de proportionnalité 2π / √g où g est l'accélération de gravité.

Ce type d'ajustement potentiel a non seulement le coefficient de détermination le plus élevé, mais la constante de l'exposant et de la proportionnalité coïncide avec le modèle physique. 

Conclusions

-L'ajustement de régression détermine les paramètres de la fonction qui vise à expliquer les données par la méthode carrée minimale. Cette méthode consiste à minimiser la somme de la différence quadratique entre la valeur et l'ajustement et la valeur YI des données pour les valeurs Xi des données. De cette façon, les paramètres de la fonction d'ajustement sont déterminés.

-Comme nous l'avons vu, la fonction d'ajustement la plus courante est la ligne, mais ce n'est pas la seule, car les ajustements peuvent également être polynomiques, potentiels, exponentiels, logarithmes et autres. 

-Dans tous les cas, le coefficient de détermination dépend des données et du type d'ajustement et est un indicatif de la bonté de l'ajustement appliqué.

-Enfin, le coefficient de détermination indique le pourcentage de variabilité totale entre la valeur et les données par rapport à la valeur ŷ de l'ajustement pour le x donné.

Les références

1. González c. Statistiques générales. Récupéré de: Tarwi.La Molina.Édu.pe
2. IACS. Institut aragonais des sciences de la santé. Récupéré de: ics-aragon.com
3. Salazar C. et Castillo S. Principes de base des statistiques. (2018). Récupéré de: dspace.Uce.Édu.CE
4. Superprof. Coefficient de détermination. Récupéré de: superprof.est
5. USAC. Manuel des statistiques descriptives. (2011). Récupéré de: statistiques.ingénierie.USAC.Édu.GT.
6. Wikipédia. Coefficient de détermination. Récupéré de: est.Wikipédia.com.