Tests d'hypothèses

Qu'est-ce que le test d'hypothèse?

La tests d'hypothèses, Dans les statistiques, il s'agit d'une procédure utilisée pour vérifier le succès d'une conjecture sur un Ville. Ces conjectures sont appelées hypothèse, qu'en principe, ils sont considérés comme vrais, jusqu'à ce que certaines preuves confirment ou le refuse.

Ces preuves sont fournies par des données d'échantillon, celles qui proviennent d'une partie importante de la population, appelée goûter. La théorie des probabilités fournit les techniques nécessaires pour contraster la véracité des hypothèses.

Des exemples d'hypothèses sont:

-La température corporelle humaine moyenne est de 36.1 ºC.

-En moyenne, un sac d'arachide salé produit dans une usine de collations pèse 50 g.

-80% des habitants d'une ville ont fait des achats en ligne au cours des 6 derniers mois.

-Les résultats des tests de QI pour les étudiants universitaires d'un établissement bien connu, ont un écart-type de 15.

-Une certaine variable aléatoire x suit une distribution de Poisson.

Les quatre premiers sont du type d'hypothèse paramétrique, Parce que ce sont des déclarations sur un paramètre de population, comme la moyenne, l'écart type ou une proportion.

D'un autre côté, la dernière hypothèse établit la distribution d'une variable aléatoire, et comme elle ne fait référence à aucun paramètre ou propriété de la population, il est dit qu'il s'agit d'une hypothèse pas paramétrique.

Hypothèse nulle et hypothèse alternative

Il existe deux types d'hypothèses avec lesquelles effectuer un test, qui servira à les contraster:

-Hypothèse nulle, indiqué comme h₀, indique que le paramètre à l'étude a une valeur établie, ou que la variable aléatoire suit une certaine distribution. Par conséquent, en exprimant symboliquement l'hypothèse nulle, le symbole de l'égalité est toujours utilisé.

-Hypothèse alternative: appelé h₁, Il affirme que le paramètre ou la distribution sont différents de ce que l'hypothèse nulle garantit, par conséquent, pour exprimer symboliquement l'hypothèse alternative, les symboles sont utilisés: ou ≠, mais jamais l'égalité.

Il peut vous servir: propriété de verrouillage de l'algèbre: démonstration, exemples

Lorsque l'hypothèse nulle est acceptée, l'hypothèse alternative est rejetée, de sorte que les deux s'excluent mutuellement.

Niveau de signification

C'est une mesure pour l'erreur qui peut être commise lors de l'exécution d'un test d'hypothèse. Il est défini comme la probabilité de rejeter l'hypothèse nulle, étant qu'il est vrai. Il est généralement indiqué avec la lettre grecque α:

α = p (rejeter h₀ Quand c'est vrai)

Les valeurs couramment utilisées pour α sont 0.01, 0.05, et 0.dix; Être le second l'utilisation la plus fréquente. Équivalent respectivement à 1%, 5% et 10% de probabilité de faire des erreurs lors du rejet H₀, Mais en tout cas, plus le niveau de signification est bas, plus le résultat du test est fiable.

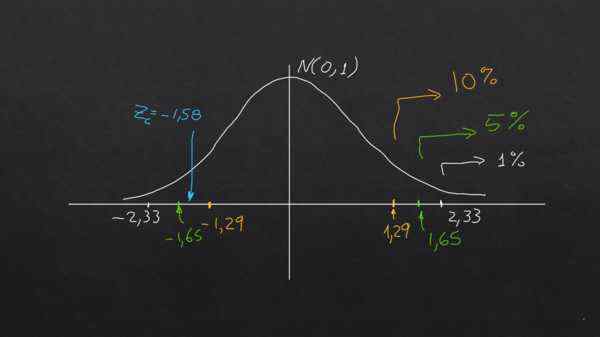
La valeur alpha (α) peut être comprise comme la fraction en pourcentage de la zone de queue droite (ou gauche), dans une distribution normale caractérisée (μ = 0 et σ = 1) et ces valeurs se produisent toujours à z = 2,33 pour α = 0.01; à z = 1,65 pour α = 1,65 et à z = 1,29 pour α = 0,1.

Étapes pour effectuer un test d'hypothèse

Étape 1

Définir respectivement les hypothèses nulles et alternatives. L'hypothèse nulle établit que le paramètre à l'étude, appelé θ, est égal à une valeur de référence, désigné θ₀:

H₀: θ = θ₀

Par exemple, si les effets d'un médicament sont étudiés sur une certaine caractéristique d'une population de souris de laboratoire, l'hypothèse nulle envisage que ce médicament ne fait aucune différence dans une telle caractéristique et que cela a une valeur constante θ₀.

Pour symboliser l'hypothèse nulle, le signe d'égalité est toujours utilisé, en revanche, l'hypothèse alternative utilise l'un des symboles ou ≠.

Dans l'exemple du médicament, l'hypothèse alternative établit que le composé a un certain effet sur la caractéristique en question. Par conséquent, c'est plus grand, inférieur ou tout simplement différent de la valeur de référence θ₀.

Peut vous servir: Notation factorielle: concept, exemples et exercices

Étape 2

Choisissez le niveau de signification approprié, qui est généralement établi à 5%, comme indiqué précédemment.

Étape 3

Déterminer la population et en extraire l'échantillon, ou échantillons, dont l'analyse servira à contraster les hypothèses et à déterminer l'acceptation ou le rejet de l'hypothèse nulle.

Étape 4

Choisissez et calculez la valeur de la statistique de l'essai pour les données collectées, à partir de laquelle les preuves nécessaires sont obtenues pour prendre la décision d'accepter ou de rejeter l'hypothèse nulle. Le choix de la statistique de l'essai dépend du paramètre sélectionné: moyenne, déviation, proportion ou autre.

La statistique de l'essai est obtenue en convertissant un paramètre d'échantillon en un score Z, un étudiant, R Pearson ou Chi Square Statistics, selon la conception expérimentale sélectionnée. Il y a des formules pour cela.

Habituellement, si le paramètre de population est la moyenne μ, la «barre X» est la moyenne de l'échantillon, l'écart type σ est connu et la taille de l'échantillon est n> 30, la statistique de test Z_C Il est calculé avec le score Z:

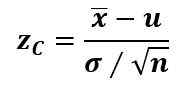
Et quand n < 30, pero σ es desconocida, se usa la t de Student.

Étape 5

Établir des critères d'acceptation ou de rejet de l'hypothèse nulle, qui peut être effectuée par deux procédures:

• À travers les valeurs p.
• Par comparaison avec les valeurs critiques.

Les valeurs de P sont équivalentes à la probabilité d'obtenir les résultats trouvés, car l'hypothèse nulle est vraie. Si ces valeurs sont faibles, l'hypothèse nulle est rejetée, si elles ne le sont pas, elle est acceptée. Dans tous les cas, les valeurs P ne constituent pas la preuve que l'hypothèse alternative est vraie.

Il convient de tenir compte du fait que dans un test d'hypothèse, il est possible de faire deux types d'erreur:

• Erreur de type I: Rejeter h₀ Quand c'est vrai. Sa probabilité est α et équivaut au niveau de signification de preuve.
• Erreur de type II: Accepter h₀ Quand c'est vraiment faux. Sa probabilité est indiquée comme β.

Il peut vous servir: quelle est la relation entre la zone du losange et le rectangle?

Étape 6

Prendre la décision d'accepter ou de rejeter l'hypothèse nulle. Si les valeurs de p sont utilisées, lorsque P < α, se rechaza H₀ Et h est accepté₁, Et sinon, H est accepté₀. L'ensemble des valeurs p < α se conoce como région critique. Si la statistique est dans cet intervalle, H est rejeté₀.

De même, une valeur critique est sélectionnée, selon le paramètre de population choisi. S'il s'agit de la moyenne, procédez comme suit:

• Test d'une queue: θ < θ₀ ou θ> θ₀
• Test de deux queues: | θ | < θ₀

Exemple résolu

Une machine fabrique des vis dont la valeur nominale doit avoir 800 millimètres de long, avec un écart-type de 5%.

Un échantillon aléatoire est prélevé, c'est-à-dire à différents jours de la semaine de production, qui totalise environ 40 vis. Lorsque la longueur moyenne de l'échantillon est calculée, la valeur de 790 millimètres est obtenue.

Déterminez si la durée moyenne est de tolérance avec des niveaux de signification respectivement de 1%, 5% et 10%.

Solution

La première consiste à calculer la statistique moyenne de test, ce qui est dans ce cas l'écart de la moyenne divisée entre l'erreur de population standard:

Zc = (790 - 800) / (40 / √40) = -1,58

Où il a été pris en compte que l'écart type de 5% correspond à 40 sur 800.

L'hypothèse nulle est que l'échantillon moyen se situe dans la tolérance autorisée au niveau de signification requis, à condition que | Zc | est inférieur à la valeur typique | zt |, sinon l'hypothèse nulle est rejetée.

Pour 1% et 5% de signification, l'hypothèse nulle est respectée, puisque | ZC | < 2,33 y |Zc| < 1,65 respectivamente.

Cependant, pour 10% de signification, il arrive que | ZC | > 1.29. C'est-à-dire à ce niveau de signification, l'hypothèse nulle n'est pas respectée.

Le graphique suivant clarifie la conclusion:

Le graphique montre que, selon le niveau de signification, la même hypothèse peut être acceptée ou rejetée avec les mêmes données. Source: F. Zapata.