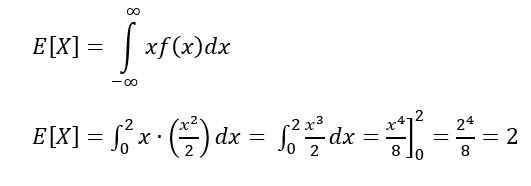Variable aléatoire continue

Nous expliquons quelle est une variable aléatoire continue, ses caractéristiques, ses exemples et un exercice résolu

Qu'est-ce qu'une variable aléatoire continue?

Ongle Variable aléatoire continue C'est une valeur numérique obtenue au hasard, qui résulte de la réalisation d'une expérience et peut prendre des valeurs infinies. Cela signifie que, connues deux valeurs consécutives de la variable, il est toujours possible de trouver une autre valeur intermédiaire entre eux.

En ayant une quantité infinie de valeurs, la collecte de valeurs variables continues n'est pas comptabilité et appartient presque toujours à l'ensemble de nombres réels.

Des exemples de ce type de variables sont la stature, le poids et la température corporelle d'une personne, mais d'innombrables d'entre eux peuvent être définis, plusieurs exemples seront trouvés ci-dessous. Contrairement à la variable aléatoire continue, il y a la variable aléatoire discrète, qui est comptabilité, comme le nombre de filles dans une famille, ou le nombre de voitures qu'une agence vend après un mois.

Les variables aléatoires discrètes suivent fréquemment la distribution de probabilité normale. Source: F. Zapata.

Une variable aléatoire continue est indiquée au moyen d'une lettre majuscule telle que le X, et les valeurs infinies que la variable prend sont les résultats possibles de l'expérience aléatoire:

X = x₁, X₂, X₃,… ∞

Chaque valeur a une certaine probabilité d'occurrence, et au modèle par lequel cette probabilité est calculée, elle est appelée distribution de probabilité.

Mais, puisque X prend des valeurs infinies, la probabilité de valeurs spécifiques de la variable ne peut pas être calculée. Il est donc nécessaire de définir une fonction f (x), appelée Fonction de distribution accumulée, ou simplement fonction de distribution, selon laquelle la probabilité accumulée est calculée à une certaine valeur ou entre deux valeurs:

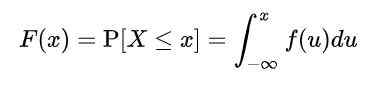
Où f (u) recevoir le nom de fonction de densité. Défini de cette manière, F (x) représente la probabilité que X est entre -∞ et X.

Caractéristiques d'une variable aléatoire continue

Les variables aléatoires continues sont complètes f (x).

La fonction de densité f (x) Doit répondre aux propriétés suivantes:

• La fonction f (x) C'est positif: f (x)> = 0
• La zone sous la courbe y = f (x) Il est toujours égal à 1, c'est-à-dire que la probabilité de survenue d'un résultat X Dans l'intervalle (-∞, + ∞) est à 100%.
• La probabilité que X soit dans l'intervalle [a, b] est calculée par l'intégrale définie suivante:

Peut vous servir: Curtosis: définition, types, formules, à quoi sert, par exemple

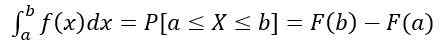
Ce qui équivaut à la zone sous la courbe y = f (x), compris entre pour et b. En outre:

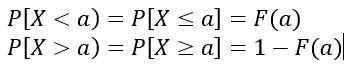
Les valeurs de f (x) Ils ne représentent pas une probabilité, donc P [x = c] = 0. Les valeurs pertinentes sont celles correspondant à la zone sous la courbe y = f (x), qui représentent une probabilité.

• En dérivant la fonction de distribution F (x) en ce qui concerne X, Est obtenu f (x).

Le graphique de f (x) Pour une variable aléatoire continue, elle est analogue au polygone de fréquence construit pour une variable statistique discrète, avec la différence que, pour la variable aléatoire, la largeur de l'intervalle devient infinitésimal.

Espoir

L'espoir est l'une des mesures caractéristiques d'une variable continue. L'espoir ou la valeur attendue de X Indique la valeur qui devrait se produire plus fréquemment et est calculée par l'intégrale suivante:

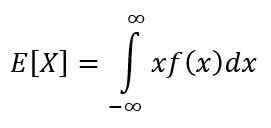
Ses propriétés sont:

• E [a∙ x] = a∙ e [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ x + b∙ y] = a∙ e [x] + b∙ e [y]

Où les montants pour et b Ce sont de vrais nombres.

Exemples

Comme indiqué précédemment, il existe de nombreuses situations dans lesquelles une ou plusieurs variables aléatoires continues peuvent être définies. Dans la science et d'autres domaines, les plus courants sont du temps, de la longueur, du poids, du volume et de la température:

Temps

Afin d'optimiser les processus et les services, des expériences sont conçues qui étudient le temps qu'ils prennent pour être effectué:

X = temps qui emmène un client à la fenêtre de la banque.

Y = ce qui prend un lieu de restauration rapide pour servir une commande.

Z = temps dans lequel une certaine réaction chimique se produit.

STAURES ET POIDS

Dans de nombreuses études sur les personnes et les animaux, les statistiques et les poids sont pertinents:

X = taille des filles dans un 6e cours. Diplôme dans chaque école d'une ville.

Peut vous servir: Congruence: figures congruentes, critères, exemples, exercices

Y = poids des bébés à la naissance dans un hôpital public.

Z = le poids des vaches dans une ferme.

Températures

La température est un paramètre pertinent dans de nombreux processus chimiques, qui prend généralement des valeurs infinies dans une certaine plage:

X = température à laquelle une certaine réaction chimique se produit, sachant que cela se produit entre 80 ºC et 120 ºC.

Exercices résolus

Exercice 1

Déterminez quelles sont les variables aléatoires continues:

1. Le nombre d'étudiants fréquentant le café de l'université.
2. Pression artérielle des patients qui viennent aux urgences.
3. Longueur des ailes d'oiseaux, d'une espèce en voie de disparition, qui habitent une réserve.
4. Le temps entre une personne et une autre est traité dans une banque.
5. Quantité de produits défectueux par mois dans une usine.
6. Taux de cholestérol chez les poulets d'une ferme.
7. Quantité de réverbères dans une rue, d'un total de 12.

Solution

1.- Le nombre d'étudiants assistés à la journée est engourdagé, par conséquent, cette variable n'est pas continue, mais discrète.

2.- C'est continu. La pression artérielle des patients peut prendre n'importe quelle valeur dans une plage donnée.

3.- Variable continue, car la longueur de l'aile d'un oiseau prend toute valeur entre un minimum et un maximum, selon l'espèce.

4.- Le temps entre le service client est variable et peut prendre n'importe quelle valeur dans une plage donnée, par exemple, entre 1 et 5 minutes.

5.- Comme le nombre de produits défectueux est comptable, c'est une variable aléatoire discrète.

6.- Cette variable est continue, car le niveau de cholestérol chez les poulets prend toute valeur dans une plage précédemment déterminée.

Peut vous servir: angles complémentaires: qui et comment ils sont calculés, exemples, exercices

7.- Discret. Le nombre de lumières d'éclairage qui fonctionnent est une quantité comptable.

Exercice 2

La variable aléatoire continue est définie X = "niveau de cholestérol " Dans une certaine variété de poulets d'une ferme, qui a la fonction de densité suivante f (x):

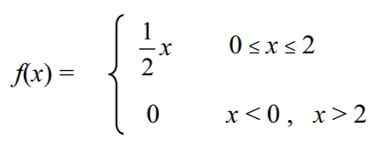
Calculez ce qui suit:

1. F (x)
2. P [x ≤2]
3. L'espoir EX]

Solution à

Selon la définition donnée au début:

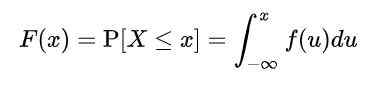
Donc, F (x) C'est une fonction en parties. Pour l'intervalle X<0, F (x) Il est égal à 0, pour les propriétés énoncées au début.

Dans l'intervalle 0≤X≤2, L'intégrale indéfinie est résolue:

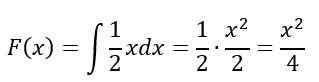
Enfin, pour l'intervalle X> 2, F (x) = 1, Selon les propriétés, donc, F (x) Il reste comme ceci:

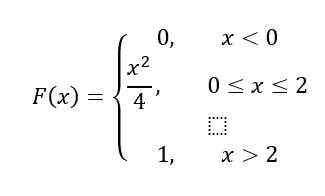
Solution B

La probabilité recherchée est F (1.2) et cOmo x = 1.2 Il se trouve entre 0≤X≤2, cette partie de F (x) pour évaluer:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Solution C

Pour calculer l'espoir ou la valeur attendue, il est utilisé: