Estimation par intervalles

Quelle est l'estimation par intervalles?

La Estimation par intervalles C'est le moyen de déterminer la plage des valeurs dans lesquelles la moyenne de la population peut être incluse, en fonction des informations d'un échantillon de taille finie, extraite au hasard de la population totale.

Il Intervalle d'estimation Il est plus bas car l'échantillon est plus grand, mais il devient plus large si le niveau ou le pourcentage de fiabilité des mêmes augmentations.

Si vous souhaitez connaître la moyenne de la population d'une certaine variable sous forme exacte, alors la population totale doit être prise en compte, quelque chose qui n'est pas toujours possible, car s'il s'agit d'une très grande population, il est coûteux d'obtenir les données de la population entière. Pour cette raison, un ou plusieurs échantillons aléatoires de la population totale sont utilisés pour prélever.

Il est basé sur l'hypothèse qu'en extrait un échantillon aléatoire, non biaisé et en tenant compte proportionnellement de toutes les strates, alors la valeur moyenne de l'échantillon doit être très proche de celle de la moyenne de la population.

La logique indique que plus les données de l'échantillon sont élevées, la différence entre la valeur moyenne de l'échantillon et la valeur de la population moyenne est plus faible.

Intervalle d'estimation

En pratique, à moins que la population complète ne soit connue, il n'est possible que, avec une certaine probabilité, l'intervalle où la moyenne de la population peut être trouvée, sur la base d'un échantillon de taille finie.

Dans le cas d'une population qui suit une distribution normale, avec Écart type σ , la Différence standard Entre la moyenne de la population μ et l'échantillon moyen de taille n est donné par:

| μ - | ≤ σ / √n

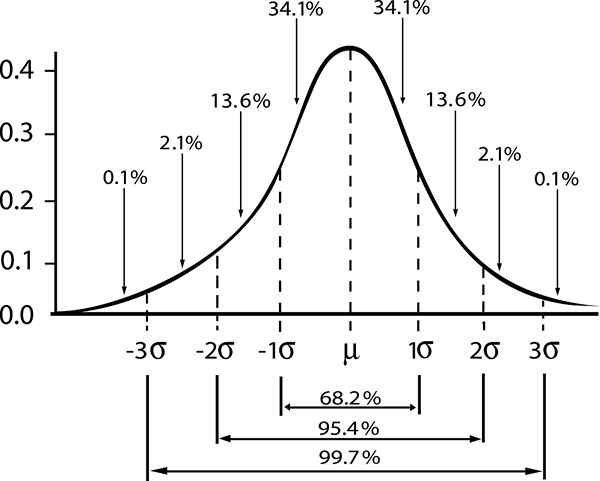
Ici, le mot "standard" indique que 68% des échantillons de taille n, Ils ont une valeur moyenne entre l'intervalle [μ - σ / √n, μ + σ / √n].

Peut vous servir: critères de divisibilité: quels sont-ils, quels sont les usage et les règles

Estimation standard

Une autre interprétation de ce qui précède serait de dire que la moyenne de la population obtenue à partir d'un échantillon de taille n et la valeur moyenne est comprise dans l'intervalle  [- σ / √n, + σ / √n], Avec 68% de probabilité.

Dans la plupart des cas réels, il n'est pas possible de connaître l'écart de population standard, donc σ Il est approximé par l'écart type de l'échantillon s, qui est calculé comme suit:

S = √ (∑ (x_Toi - )² / √ (n-1).

De là, vous obtenez l'intervalle qui pourrait contenir la moyenne de la population avec un niveau de confiance de 68% (niveau de confiance standard), donné par:

  -s / √n ≤ μ ≤ + s / √n

Cet intervalle de mesure de la population est connu sous le nom intervalle d'estimation standard et a été obtenu uniquement avec les données disponibles en taille n.

D'après la formule précédente, il s'ensuit que si vous vouliez renforcer l'intervalle d'estimation en deux, c'est nécessaire quadruple La taille de l'échantillon.

Estimation par intervalles de confiance

Dans certaines études, un niveau standard de 68% peut être insuffisant, alors il est nécessaire de déterminer les intervalles avec un niveau de confiance arbitraire γ.

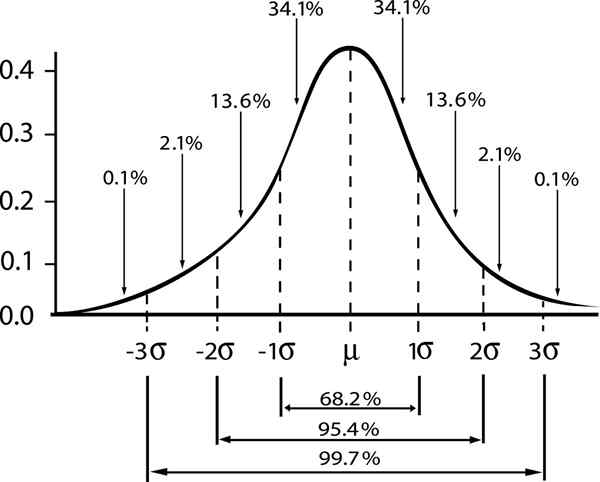La relation entre la marge de fiabilité et l'intervalle dans une distribution gaussienne est indiquée

Si nous désignons ε L'erreur standard s / √n, puis l'erreur d'estimation pour un niveau de confiance γ sera donné par:

E = zγ⋅ε.

Où Zγ Il s'agit d'un nombre par lequel l'erreur standard est multipliée et obtient ainsi la marge d'erreur avec un niveau de confiance arbitraire γ.

Pour obtenir le facteur Zγ, procédez comme suit:

Il peut vous servir: Nombres rationnels: propriétés, exemples et opérations

Étape 1

Est l'appel niveau de signification α correspondant au niveau de confiance γ par la formule suivante:

α = 1 - γ

Étape 2

La valeur est déterminée:

Il s'agit de la fréquence accumulée dans une distribution normale caractérisée N (0,1) Dans l'intervalle (-∞, Zγ ]].

Étape 3

Il efface Zγ L'équation:

N (zγ) = 1 - α / 2

Comme il s'agit d'une équation intégrale, cette clairance est obtenue à partir des tables de distribution normales, en utilisant la méthode d'interpolation linéaire.

Étape 4

Alternativement à l'utilisation de tables, les fonctions statistiques incorporées dans les feuilles de calcul telles que Exceller, soit Feuille Google. Ces programmes intègrent une fonction inverse normale N^-1, Pour que le facteur de correction Zγ Il est obtenu directement en évaluant cette fonction inverse:

Zγ = n^-1(1 - α / 2).

Intervalles de confiance typiques

Les niveaux de confiance les plus fréquemment utilisés sont:

• Zγ = 1; Niveau de confiance standard γ = 0,68.
• Zγ = 2; un niveau de confiance γ = 0,95 (ou niveau de signification 5%).
• Zγ = 3; un niveau de confiance γ = 0,997 (ou 0,3% de niveau de signification)

Exemples

Exemple 1

Déterminez l'intervalle de poids moyen des nouveau-nés au cours du mois d'août dans une grande ville basée sur un échantillon aléatoire de 100 bébés, dans lequel un poids moyen de 3100 grammes a été obtenu avec un écran d'échantillon de l'écran S = 1500 grammes.

Solution

Premièrement, l'erreur standard de l'échantillon est déterminée:

ε = s / √n = (1500 g) / √100 = 150 g.

Par conséquent, à partir de cet échantillon, on peut en déduire que le poids moyen des bébés nés en août dans cette ville se situe entre 2950 g et 3250 g, avec une probabilité de 68%.

Exemple 2

Supposons la taille de l'échantillon de bébés nés le même mois d'août et dans la même ville d'exemple 1. Le poids moyen de l'échantillon est de 3100 g avec une dispersion standard de 1500 g. 

Il peut vous servir: décomposition de nombres naturels (exemples et exercices)

Il est invité à estimer l'intervalle de poids moyen des nouveau-nés de cette ville, de ce nouvel échantillon.

Solution

Maintenant, l'erreur standard diminue du facteur 1 /√2, Ainsi, la nouvelle erreur standard du poids moyen sera de 106 g.

Il peut ensuite être estimé à partir de ce nouvel échantillon que le poids moyen des nouveau-nés est composé de 2994 g à 3206 g, avec une probabilité de 68%.

Exercices

Exercice 1

Déterminez la plage de poids moyenne des nouveau-nés en août, à partir de l'échantillon spécifié dans l'exemple 1, avec une probabilité de 95%.

Solution

Un niveau de fiabilité de 95% double la plage de poids moyenne, par rapport à un niveau de fiabilité de 68%.

Par conséquent, le poids moyen des nouveau-nés est inclus dans la fourchette de 2800 grammes à 3400 grammes avec une certitude à 95%.

Exercice 2

Estimer avec un niveau de confiance de 99,7% L'intervalle dans lequel le poids moyen des nouveau-nés d'une grande ville sera trouvé, si un échantillon est disponible avec le poids moyen de 100 bébés égaux à 3100 g, et avec un écart d'échantillon standard s = 1500 g.

Solution

La marge d'erreur de poids moyenne, avec 99,7% de certitude, sera triple de l'erreur moyenne, c'est-à-dire:

3 * 1500 /√100.

Ensuite, il est déduit, de cet échantillon, que le poids moyen des nouveau-nés sera inclus dans l'intervalle: 2650 grammes à 3550 grammes, avec un niveau de certitude de 99,7%. 

De ce résultat, il est observé comme pour un plus grand niveau de certitude augmente l'incertitude du poids moyen à un intervalle beaucoup plus large.