Propriété de la propriété, exemples

La Propriété de verrouillage de l'algèbre Il s'agit d'un phénomène qui relie deux éléments d'un ensemble avec une opération, où la condition nécessaire est qu'après les 2 éléments sous cette opération, le résultat appartient également à l'ensemble initial.

Par exemple, si même les nombres sont pris dans son ensemble et une somme en tant qu'opération, une serrure de ce jeu en ce qui concerne la somme est obtenue. En effet.

Source: Unsetpash.com

[TOC]

Caractéristiques

Il existe de nombreuses propriétés qui déterminent les espaces ou les corps algébriques, tels que les structures ou les anneaux. Cependant, la propriété Lock est l'une des plus connues dans l'algèbre de base.

Toutes les applications de ces propriétés ne sont pas basées sur des phénomènes ou des éléments numériques. De nombreux exemples de tous les jours peuvent fonctionner à partir d'une approche théorique algébrique pure.

Un exemple peut être les citoyens d'un pays qui assument une relation juridique de toute nature, comme la société commerciale ou le mariage entre autres. Après cette opération ou cette gestion, ils sont toujours citoyens du pays. Ainsi, les opérations de citoyenneté et de gestion en ce qui concerne deux citoyens représentent une serrure.

Algèbre numérique

En ce qui concerne les chiffres, il existe de nombreux aspects qui ont été une raison d'étude dans différents courants de mathématiques et d'algèbre. À partir de ces études, un grand nombre d'axiomes et de théorèmes ont émergé qui servent de base théorique de la recherche et des œuvres contemporaines.

Si vous travaillez avec des ensembles numériques, nous pouvons établir une autre définition valide de la propriété Lock. On dit qu'un ensemble A est la serrure d'un autre ensemble B si A est le plus petit ensemble qui contient tous les ensembles et opérations qui maison B.

Peut vous servir: propriété distributive

Manifestation

La démonstration de verrouillage est appliquée aux éléments et opérations présentes dans l'ensemble des nombres N réels.

Soit A et B deux nombres qui appartiennent à l'ensemble R, la serrure de ces éléments est définie pour chaque opération contenue dans R.

Ajout

- Sum: ∀ a ˄ b ∈ R → A + b = c ∈ R

C'est la façon algébrique de dire que Pour tous A et B qui appartiennent à des nombres réels, il doit être la somme d'un plus b est égal à C, qui appartient également au réel.

Il est facile de vérifier si cette proposition est vraie; Il suffit de faire la somme entre tout nombre réel et de vérifier si le résultat appartient également aux nombres réels.

3 + 2 = 5 ∈ R

-2 + (-7) = -9 ∈ R

-3 + 1/3 = -8/3 ∈ R

5/2 + (-2/3) = 11/6 ∈ R

Il est observé que la condition de verrouillage est remplie pour des nombres réels et la somme. De cette façon, il peut être conclu: La somme des nombres réels est une serrure algébrique.

Multiplication

- Multiplication: ∀ a ˄ b ∈ R → A . B = c ∈ R

Pour tous A et B qui appartiennent aux vrais, la multiplication de A pour B est égale à C, qui appartient également au réel.

Lors de la vérification avec les mêmes éléments de l'exemple précédent, les résultats suivants sont observés.

3 x 2 = 6 ∈ R

-2 x (-7) = 14 ∈ R

-3 x 1/3 = -1 ∈ R

5/2 x (-2/3) = -5/3 ∈ R

Il s'agit d'une preuve suffisante pour conclure que: La multiplication des nombres réels est un verrou algébrique.

Cette définition peut être étendue à toutes les opérations de nombres réels, bien que nous trouverons certaines exceptions.

Source: Pixabay.com

Cas spéciaux en r

Division

Dans un cas particulier, la division est observée, où l'exception suivante est appréciée:

Peut vous servir: Probabilité classique: calcul, exemples, exercices résolus

∀ a ˄ b ∈ R → a / b ∉ r ↔ b = 0

Pour tous A et B qui appartiennent à R Il doit entre B n'appartient pas à la reais si et seulement si B est égal à zéro.

Cette affaire fait référence à la restriction de ne pas pouvoir diviser entre zéro. Parce que zéro appartient aux nombres réels, il est conclu que: lLa division n'est pas une serrure dans le réel.

Radio

Il existe également des opérations de potentialisation, plus spécifiquement celles du dépôt, où des exceptions sont présentées pour les pouvoirs radicaux de l'indice de couple:

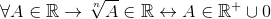; Avec n par

Pour tout ce à quoi il appartient au royal.

De cette façon, il est indiqué que les racines uniformes ne s'appliquent qu'aux réelles positives et il est conclu que la potentialisation n'est pas une serrure en R.

Logarithme

Il est approuvé pour la fonction logarithmique, qui n'est pas définie pour les valeurs plus petites ou égales à zéro. Pour vérifier si le logarithme est un verrouillage R procède comme suit:

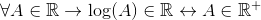
Pour tout ce à quoi il appartient à la reais, le logarithme de A appartient à la reais, si et seulement s'il appartient au réel positif.

Lorsque les valeurs négatives et nulles qui appartiennent également à R sont exclues, il peut être confirmé que:

Le logarithme n'est pas une serrure de nombres réels.

Exemples

Vérifiez le verrou pour la somme et la soustraction des nombres naturels:

Somme en n

La première chose est de vérifier la condition de verrouillage pour différents éléments de l'ensemble donné, où s'il est observé que certains éléments se cassent avec la condition, l'existence de verrouillage peut être automatiquement refusée.

Peut vous servir: Radio de convergence: définition, exemples et exercices résolus

Cette propriété est remplie pour toutes les valeurs possibles de A et B, comme observé dans les opérations suivantes:

1 + 3 = 4 ∈ N

5 + 7 = 12 ∈ N

1000 + 10000 = 11000 ∈ N

Il n'y a pas de valeurs naturelles qui brisent la condition de verrouillage, il est donc conclu:

La somme est une serrure en n.

Soustrait en n

Des éléments naturels sont recherchés capables de briser la condition; A - B appartient aux indigènes.

En fonctionnement, il est facile de trouver des paires d'éléments naturels qui ne répondent pas à l'état de verrouillage. Comme par exemple:

7 - 10 = -3 ∉ A n

De cette façon, nous pouvons conclure que:

La soustraction n'est pas une serrure de l'ensemble des nombres naturels.

Exercices proposés

1-Samp.

2-explaçant si l'ensemble des nombres réels est une serrure de l'ensemble des nombres.

3-détermine quel ensemble numérique peut être le verrouillage des nombres réels.

4 échantillonnez la propriété de verrouillage pour l'ensemble des nombres imaginaires, en ce qui concerne la somme, la soustraction, la multiplication et la division.

Les références

1. Panorama of Pure Mathematics: The Bourbakist Choice. Jean Dieudonné. Reverte, 1987.
2. Théorie des nombres algébriques. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. Université nationale autonome du Mexique, 1975.
3. Algèbre linéaire et ses applications. Sandra Ibeth Ochoa García, Eduardo Guérrez González.
4. Structures algébriques V: théorie du corps. Héctor A. Merklen. Organisation des États américains, Secrétariat général, 1979.
5. Introduction à l'algèbre commutative. Michael Francis Atiyah, je. g. Macdonald. Reverte, 1973.