Prisme carré

Nous expliquons ce qu'est un prisme quadrangulaire, ses caractéristiques, les visages, les sommets, les bords, comment calculer le volume, les exemples et les exercices résolus

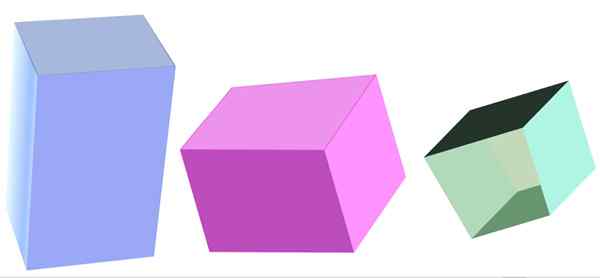
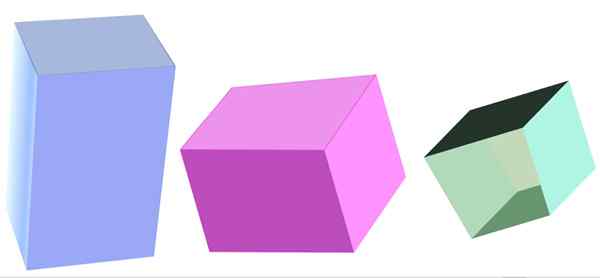Divers types de prisme quadrangulaire. Source: F. Zapata

Qu'est-ce qu'un prisme quadrangulaire?

Il Prisme carré Il s'agit d'une figure géométrique à trois dimensions de la famille Polyèdros. Il est composé de deux faces égales et parallèles, avec la forme d'un quadrilatère, comme base, et quatre parallélogrammes sur les côtés, pour un total de six faces.

Il existe plusieurs critères pour les classer, car il existe de nombreuses possibilités pour la forme des visages et de l'inclinaison. Par exemple, il y a Prismes à domicile droit et les prismes quadrangulaires inclinés.

Dans le premier cas, les côtés sont perpendiculaires à la base, puis ce sont des rectangles ou des carrés. Dans le deuxième cas, les faces latérales sont inclinées par rapport à la base, par conséquent, elles ne peuvent pas être des rectangles ou du carré.

De plus, le prisme quadrangulaire peut être régulier ou irrégulier, selon la base est un quadrilatère régulier ou irrégulier. Le quadrilatère ordinaire est le carré, dont les quatre côtés et ses quatre angles mesurent le même .

Un exemple de prisme spécial à domicile est le parallélépipé, dont les bases sont des parallélogrammes. Les formes des boîtes et des briques sont inspirées des prismes quadrangulaires, donc de bons exemples de la façon d'utiliser cette figure géométrique dans les applications pratiques.

Caractéristiques du prisme quadrangulaire

Parmi les caractéristiques les plus importantes du prisme quadrangulaire, figurent les suivants:

• Leurs visages ont une forme de polygone.
• Il a un total de 6 faces (2 bases et 4 côtés), 12 bords ou bords et 8 sommets (coins).
• Les faces latérales peuvent être en forme: carré, rectangle, parallélogramme, losange ou rhomboïde.
• Ses côtés peuvent être droits (forme de 90 ° avec les bases) ou inclinés (il y a un angle inférieur à 90 ° du côté interne).
• Les visages latéraux des prismes droits ne peuvent être que carrés ou rectangles.
• Les bases de prisme reçoivent également le nom de des lignes directrices.
• Si la base est un quadrilatère régulier, le prisme quadrangulaire est également régulier. Comme une figure plate est régulière si tous ses côtés ont la même mesure, la seule possibilité est que les bases sont carrées.
• Lorsque la base du prisme est tout autre quadrilatère différent du carré, alors le prisme est considéré comme irrégulier.
• Le prisme quadrangulaire ordinaire peut être enregistré dans un cylindre.

Peut vous servir: statistiques inférentielles: historique, caractéristiques, à quoi sert, des exemples

Éléments du prisme quadrangulaire

Les cinq éléments du prisme quadrangulaire sont communs à tous les prismes:

• Bases, constitué de deux quadrilatéraux identiques et parallèles.
• Visages latéraux, sont les quatre parallélogrammes qui bordent la figure.
• Sommets ou coins, points communs qui ont trois côtés adjacents du prisme.
• Bords ou bords, segment commun qui ont deux faces adjacentes.
• Hauteur: C'est la longueur d'un segment perpendiculaire avec des extrémités dans les bases. Lorsque le prisme est droit, la hauteur coïncide avec la mesure des bords latéraux.
• Section droite, zone d'intersection entre le prisme et un plan qui forme 90º avec les bords latéraux.

L'image suivante montre chacun de ces éléments pour un prisme quadrangulaire droit:

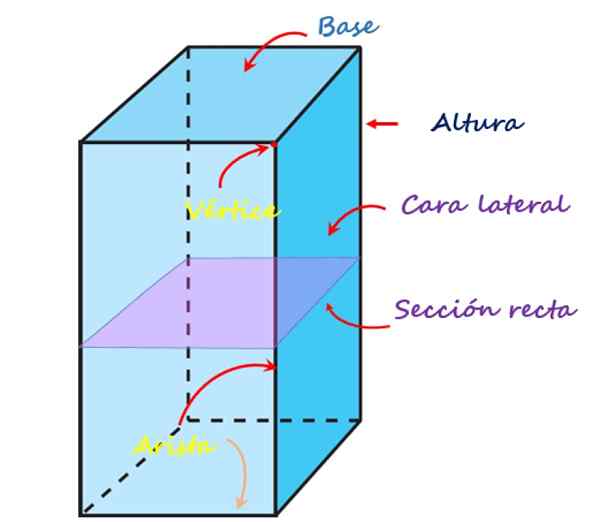Les éléments du prisme quadrangulaire. Source: F. Zapata

Visages, sommets et bords

Les visages, les sommets et les bords: les sommets et les bords:

Visages

Les visages du prisme font un total de 6: les 2 bases identiques sous la forme d'un quadrilatère et des 4 côtés les plus ou des visages sous forme de parallélogramme.

Sommets

Ce sont les coins de la figure, le point où viennent trois visages adjacents.

Bords

Ce sont les segments d'intersection entre les visages du prisme. Les bords sont classés comme:

• Bords de base, Segments communs entre les bases et les faces latérales.
• Bords latéraux, Comme son nom l'indique, ce sont les segments courants parmi les faces latérales.

La figure supérieure montre les deux types d'arêtes, désignées avec différentes flèches de couleur. Le nombre d'arêtes n_POUR peut être déterminé avec le Théorème d'Euler du polyèdros, qui relie le nombre d'arêtes à celle des visages n_C et les sommets n_V:

Peut vous servir: fonctions mathématiques

N_POUR = N_C + N_V −2

Pour le prisme quadrangulaire n_C = 6 et n_V = 8, donc:

N_POUR = 6 + 8 −2 = 12

Par conséquent, le nombre de bords ou de bords du prisme quadrangulaire est 12.

Comment calculer le volume d'un prisme quadrangulaire?

Le volume du prisme est compris comme la partie de l'espace verrouillée par elle et est mesurée en unités cubes, qui peuvent être des mètres cubes, des centimètres cubes, des pieds cubes ou d'autres appropriés, à condition qu'ils soient de longueur au cube.

Le volume V est toujours une quantité positive, et dans le cas de tout prisme quadrangulaire, il est donné par le produit entre la base de la base à_b et hauteur h:

V = a_b × H

Yo) Volume de prisme quadrangulaire régulier

Puisque les bases sont carrées et que le carré du carré est son côté ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ carré:

POUR_b = ℓ²

Ensuite, le volume du prisme dont la hauteur est "H" est:

V = ℓ² × H

Ii) Volume de prisme quadrangulaire irrégulier

Cela dépend de la forme de la base et de la hauteur "h" du prisme:

1.- Prisme de base rectangulaire

La zone des côtés rectangle "A" et "B" est:

POUR_b = A × b

Le volume est donc:

V = a × b × h

2.- Prisme de base habidale

La zone du losange est le semi-produit de ses diagonales «D» et «D»:

Et le volume est:

3.- Prisme de base en forme de Romboïde

La zone de base en forme de rhomboïde est le produit de sa base "B" et de sa hauteur relative "H_r"À cette base, qui est le segment perpendiculaire qui va de cette base au côté parallèle.

POUR_b = B × h_r

Par conséquent, le volume du prisme avec cette base est:

Peut vous servir: quelle est la gamme de statistiques? (Avec des exemples)

V = b × h_r × H

4.- Prisme de base trapézoïdale

Étant donné que la zone du trapèze est le semi-site des côtés parallèles "A" et "B", multiplié par sa hauteur "C":

Le volume du prisme trapézoïdal est:

5.- Prisme de base en forme de trapézoïde

La zone d'un trapèze symétrique est le semi-produit de ses diagonales d et d, donc:

Dans ce cas, le volume du prisme est:

Exercice résolu

Un prisme quadrangulaire de base trapézoïdale a un volume de 648 cm³. Les côtés parallèles de la mesure trapézoïdale A = 10 cm et b = 5 cm, tandis que la hauteur du trapèze est C = 6 cm. Avec ces données, trouvez la hauteur du prisme.

Solution

Étant donné que les dimensions de la base ont, votre zone peut être facilement calculée:

Et de la formule:

V = a_b × H

«H» est éliminé, la hauteur du prisme, car son volume est connu:

H = v / a_b = 648 cm³ / 45 cm² = 14.4 cm

Exemples

Prisme ou cube rectangulaire

Les six visages de ce prisme droit sont carrés ou rectangulaires. Les boîtes sont des exemples de prismes rectangulaires, une forme qui est également utilisée dans de nombreux objets et constructions tels que les bâtiments.

cube

Un cube est un prisme quadrangulaire régulier, dont les six côtés sont en forme de carré, par exemple, un dés ou le jeu de cube Rubik de bien connu.

Le cube fait partie du groupe de solides platoniques, des figures géométriques qui remplissent deux conditions. Le premier est que chaque visage est un polygone ordinaire et le second est que chaque sommet a en commun le même nombre de faces.

Le cube rencontre les deux conditions, car leurs visages ont une forme carrée, qui est un polygone ordinaire. Et dans chacun des huit sommets du cube, trois faces du même converge.

Les solides platoniques restants sont le tétraèdre, l'octaèdre, le Dodécadro et l'Icosaedro.