Cousins ​​relatifs ce que sont, des explications, des exemples

Il s'appelle cousins ​​relatifs (Coprmimos ou cousins ​​les uns par rapport aux autres) à n'importe quelle paire de nombres entiers qui n'ont pas de diviseur commun, sauf 1. En d'autres termes, deux nombres entiers sont des cousins ​​relatifs si dans leur rupture en nombres premiers, ils n'ont aucun facteur commun.

Par exemple, si les 4 et 25 sont choisis, les décompositions des facteurs premiers de chacun sont respectivement de 2² et 5². Comme on peut le voir, ils n'ont aucun facteur commun, donc 4 et 25 sont des cousins ​​relatifs.

D'un autre côté, si vous choisissez 6 et 24, lorsque vous effectuez leur panne dans des facteurs premiers, il est obtenu que 6 = 2 * 3 et 24 = 2³ * 3.

Comme on peut le voir, ces deux dernières expressions ont au moins un facteur commun, par conséquent, ce ne sont pas des cousins ​​relatifs.

Caractéristiques des cousins ​​relatifs

Un détail avec lequel les soins doivent.

D'un autre côté, la définition ci-dessus peut être résumé comme suit: Deux entiers «A» et «B» sont des cousins ​​relatifs si, et seulement, le diviseur commun maximum de ceux-ci est 1, c'est-à-dire MCD (A, B ) = 1.

Deux conclusions immédiates de cette définition sont que:

-Si "a" (ou "b") est un nombre premier, alors mcd (a, b) = 1.

-Si "a" et "b" sont des nombres premiers, alors mcd (a, b) = 1.

Autrement dit, si au moins l'un des nombres choisis est un nombre premier, alors la paire de nombres est des cousins ​​relatifs.

Autres caractéristiques

Les autres résultats utilisés pour déterminer si deux nombres sont des cousins ​​relatifs sont:

-Si deux nombres entiers sont consécutifs, alors ce sont des cousins ​​relatifs.

-Deux nombres naturels "a" et "b" sont des cousins ​​relatifs si, et seulement si, les nombres "(2 ^ a) -1" et "(2 ^ b) -1" sont des cousins ​​relatifs.

-Deux nombres entiers "a" et "b" sont des cousins ​​relatifs si, et seulement si, lors de la graphique en graphiquement le point (a, b) dans le plan cartésien, et construisez la ligne qui passe par l'origine (0,0) et (A (A , b), cela ne contient aucun point avec des coordonnées entières.

Exemples

1.- Considérez les nombres entiers 5 et 12. Les décompositions des facteurs premiers des deux nombres sont: 5 et 2² * 3 respectivement. En conclusion, MCD (5,12) = 1, par conséquent, 5 et 12 sont des cousins ​​relatifs.

2.- Laissez les chiffres -4 et 6. Alors -4 = -2² et 6 = 2 * 3, de sorte que le MCD (-4,6) = 2 ≠ 1. En conclusion -4 et 6 ne sont pas des cousins ​​relatifs.

Si la ligne qui passe par les paires ordonnées (-4,6) et (0,0), et pour déterminer l'équation de ladite ligne, peut être vérifiée que cela passe par le point (-2,3).

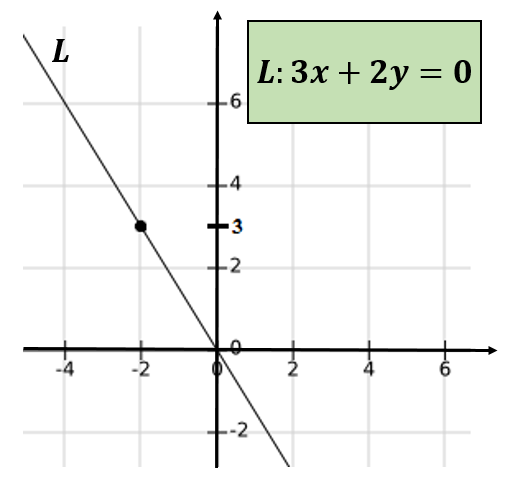
Encore une fois, il est conclu que -4 et 6 ne sont pas des cousins ​​relatifs.

3.- Les numéros 7 et 44 sont des cousins ​​relatifs et peuvent être conclus rapidement grâce à ce qui a été dit ci-dessus, car 7 est un nombre premier.

4.- Considérez les chiffres 345 et 346. Étant deux nombres consécutifs, il est vérifié que MCD (345 346) = 1, par conséquent, 345 et 346 sont des cousins ​​relatifs.

5.- Si les nombres 147 et 74 sont pris en compte, ce sont des cousins ​​relatifs, depuis 147 = 3 * 7² et 74 = 2 * 37, donc le MCD (147,74) = 1.

6.- Les nombres 4 et 9 sont des cousins ​​relatifs. Pour le démontrer, vous pouvez utiliser la deuxième caractérisation mentionnée ci-dessus. En effet, 2 ^ 4 -1 = 16-1 = 15 et 2 ^ 9-1 = 512-1 = 511.

Les nombres obtenus sont de 15 et 511. Les décompositions dans les facteurs premiers de ces nombres sont respectivement de 3 * 5 et 7 * 73, de sorte que MCD (15,511) = 1.

Comme vous pouvez le voir, l'utilisation de la deuxième caractérisation est un travail plus long et plus laborieux pour le vérifier directement.

7.- Considérez les nombres -22 et -27. Alors ces nombres peuvent être réécrits comme suit: -22 = -2 * 11 et -27 = -3³. Par conséquent, le MCD (-22, -27) = 1, donc -22 et -27 sont des cousins ​​relatifs.