Parallélépipède

Les parallèles sont des figures géométriques à six faces, où les opposés sont parallèles les uns aux autres. Exemple: une brique, une boîte à chaussures, un seau, etc.

Qu'est-ce qu'un parallélépipé?

UN parallélépipède C'est un corps géométrique formé par six faces, dont la caractéristique principale est que tous ses visages sont des parallélogrammes et que ses faces opposées sont parallèles aux autres. C'est un polyèdre commun dans notre vie quotidienne, car nous pouvons le trouver dans des boîtes à chaussures, la forme d'une brique, la forme d'un micro-ondes, etc.

Étant un polyèdre, le parallélépipe contient un volume fini et tous ses visages sont plats. Il fait partie du groupe de prismes, qui sont les polyèdres dans lesquels tous ses sommets sont contenus dans deux plans parallèles.

Éléments du parallélépipant

Visages

Ce sont chacune des régions formées par des parallélogrammes qui limitent le parallélépice. Un parallélépipé a six faces, où chaque visage a quatre faces adjacentes et un contraire. De plus, chaque visage est parallèle à son contraire.

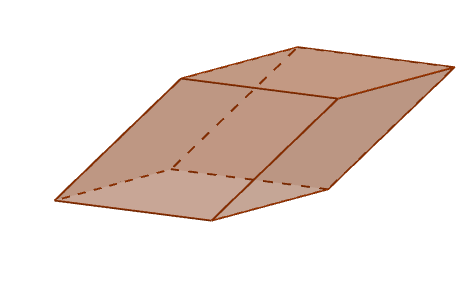Perspective d'un parallélépice

Bords

Ils sont le côté commun de deux faces. Au total, un parallélépipe a douze bords.

Sommet

C'est le point commun de trois faces qui sont adjacentes deux à deux. Un parallélépipé a huit sommets.

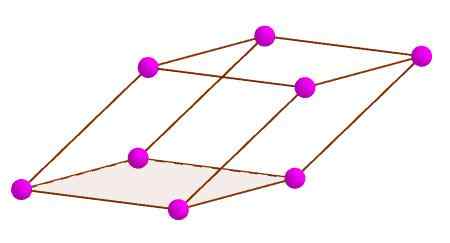Sommets d'un parallélépice

Diagonale

Compte tenu de deux faces d'un parallélépipée en face de l'autre, nous pouvons dessiner un segment de ligne qui va du sommet d'un visage au sommet opposé de l'autre.

Ce segment est connu sous le nom de diagonale parallélépipée. Chaque parallélépipée a quatre diagonales.

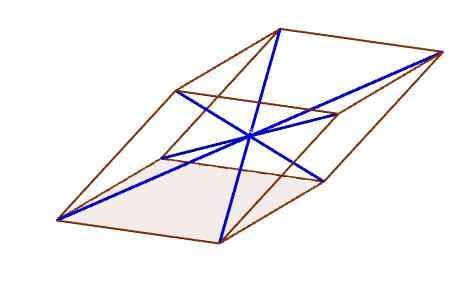Diagonales d'un parallélépice

centre

C'est le moment où toutes les diagonales se croisent.

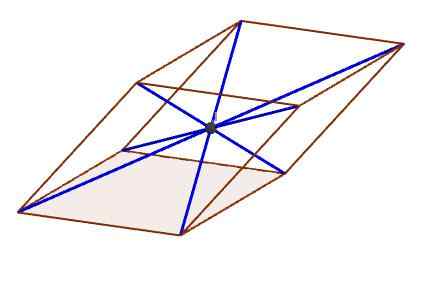Le point de la figure indique le centre, où toutes les diagonales se croisent

Caractéristiques du parallélépipant

Comme nous l'avons déjà mentionné, ce corps géométrique a douze bords, six faces et huit sommets.

Dans un parallélépipé, trois ensembles formés par quatre bords peuvent être identifiés, qui sont parallèles les uns aux autres. De plus, les bords de ces ensembles sont également conformes à la propriété d'avoir la même longueur.

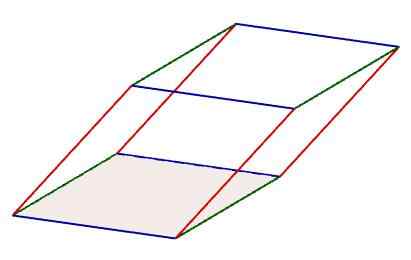Caractéristiques du parallélépipant

Une autre propriété posée.

De plus, les parallélépipes, étant des polyèdros convexes, conformes au théorème d'Euler pour les polyèdros, ce qui nous donne une relation entre le nombre de visages, le nombre de bords et le nombre de sommets. Cette relation est donnée sous la forme de l'équation suivante:

C + V = A + 2

Cette fonctionnalité est connue sous le nom de caractéristique d'Euler. Où c est le nombre de visages, et le nombre de sommets et le nombre d'arêtes.

Types de parallèles

Nous pouvons classer les parallélépípédos en fonction de leurs visages, sur les types suivants:

Orthoedro

Ce sont les parallélépípédos où leurs visages sont constitués de six rectangles. Chaque rectangle est perpendiculaire avec ceux avec lesquels il partage le bord. Ils sont les plus courants dans notre vie quotidienne, ce qui est la forme habituelle de chaussures et de boîtes de briques.

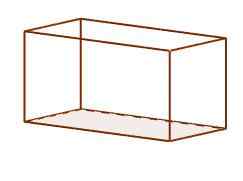Orthoedro parallélépipée

Cube ordinaire ou hexaedro

Ceci est un cas particulier de la précédente, où chacun des visages est un carré.

Peut vous servir: ellipseCube ordinaire ou hexaedro

Le cube fait également partie des corps géométriques appelés solides platoniciens. Un solide platonique est un polyèdre convexe, de sorte que ses visages et ses angles internes sont égaux les uns aux autres.

Romboedro

C'est un parallélépipé qui a un losange. Ces rhombes sont toutes égales les unes avec les autres, car elles partagent des bords.

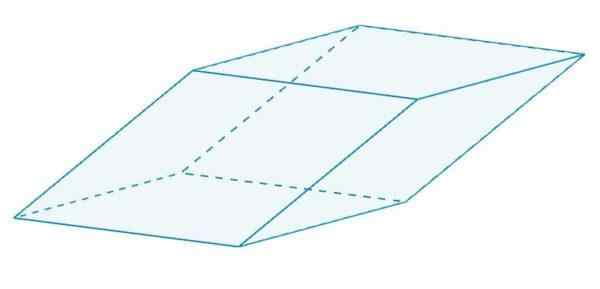Un Romboedro

Romboiedro

Ses six visages sont Rhomboid. Rappelons qu'un rhomboïde est un polygone à quatre faces et quatre angles qui sont égaux deux à deux. Les rhomboïdes sont les parallélogrammes qui ne sont ni carrés, ni les rectangles, ni les rhombus.

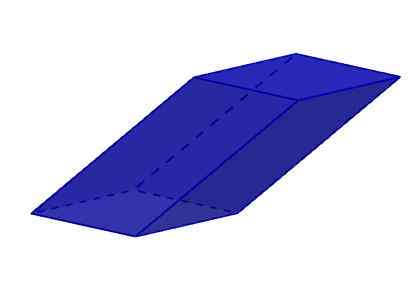Romboiedro

D'un autre côté, les parallélépipes obliques sont ceux dans lesquels au moins une hauteur ne correspond pas à son bord. Dans cette classification, nous pouvons inclure des rhomboedros et des rhomboiedros.

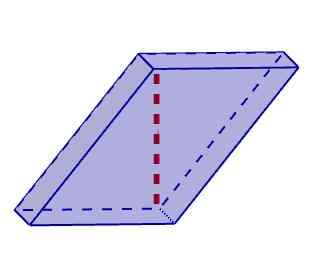Parallélépipé oblique

Calcul diagonal

Pour calculer la diagonale d'un Orthoedro, nous pouvons utiliser le théorème de Pythagore pour R³.

Rappelez-vous qu'un Orthoedro a la caractéristique que chaque côté est perpendiculaire avec les côtés qui partagent le bord. De ce fait, nous pouvons déduire que chaque bord est perpendiculaire à ceux qui partagent le sommet.

Pour calculer la longueur d'une diagonale d'un orthoedro, nous procédons comme suit:

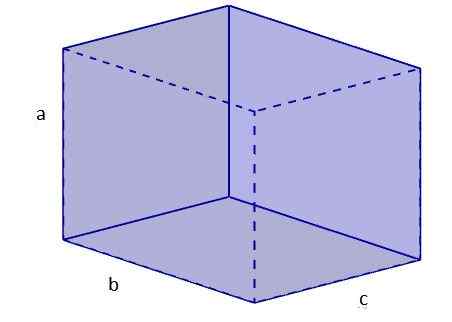
1. Nous calculons la diagonale de l'un des faces, que nous allons mettre par base. Pour cela, nous utilisons le théorème de Pythagore. Nomnons cette diagonale d_b.

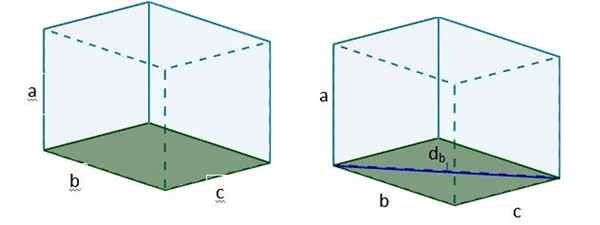
2. Puis avec D_b Nous pouvons former un nouveau triangle rectangle, de sorte que l'hypoténuse dudit triangle est la diagonale D recherchée.

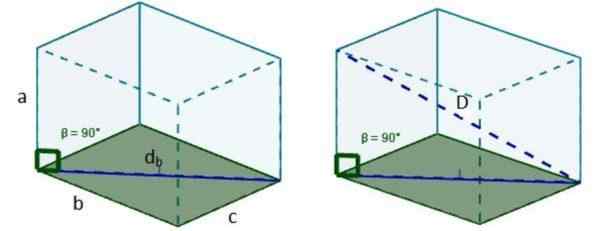
3. Nous utilisons à nouveau le théorème de Pythagore et nous avons que la longueur de cette diagonale est:

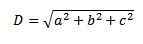
Une autre façon de calculer la diagonale d'une manière plus graphique est la somme des vecteurs libres.

Rappelons que deux vecteurs libres A et B sont ajoutés en plaçant la queue du vecteur B avec la pointe du vecteur a.

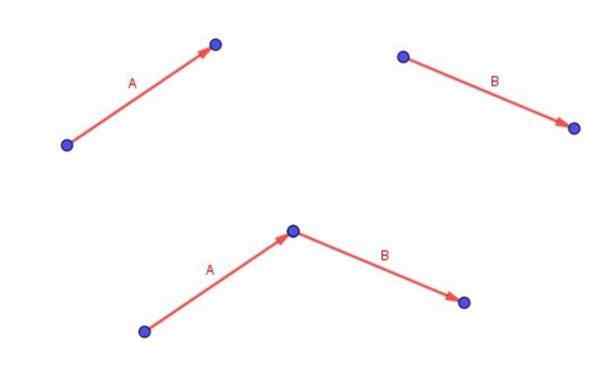
Le vecteur (A + B) est celui qui commence dans la queue de A et se termine à la pointe de B.

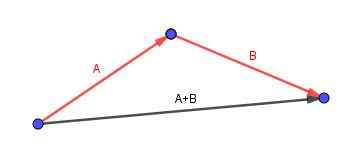
Considérer un parallélépipé auquel nous voulons calculer une diagonale. Nous identifions les bords avec des vecteurs orientés pratiques.

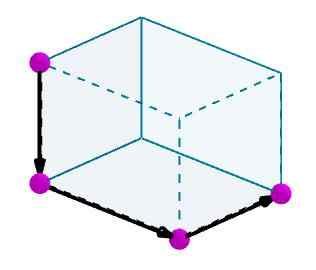
Ensuite, nous ajoutons ces vecteurs et le vecteur résultant sera la diagonale du parallèle.

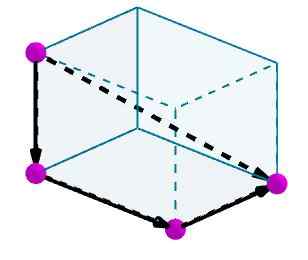
Zone d'un parallèle

La zone d'un parallélépipée est donnée par la somme de chacune des zones de ses visages.

Si nous déterminons l'un des côtés comme base,

POUR_L + 2e_B = Superficie totale

Où_L Il est égal à la somme des zones de tous côtés adjacentes à la base, appelée la zone latérale et à_B C'est la zone de base.

Selon le type de parallélépipé avec lequel nous travaillons, nous pouvons réécrire cette formule.

Zone d'un orthoedro

Est donné par la formule

A = 2 (ab + bc + ca).

Exemple 1

Compte tenu de l'orthoedro suivant, avec les côtés A = 6 cm, b = 8 cm et c = 10 cm, calculez la zone parallélépipée et la longueur de sa diagonale.

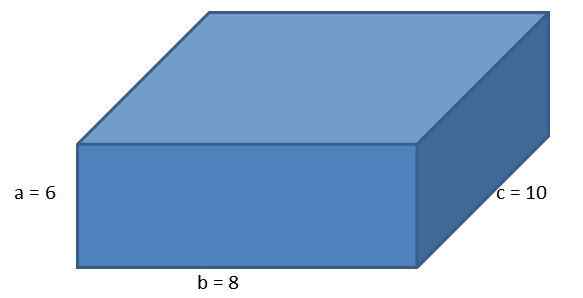
En utilisant la formule pour la zone d'un Orthoedro, nous devons

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Notez que comme un Orthoedro est la longueur de l'une de ses quatre diagonales est la même.

Il peut vous servir: Intégrale indéfinie: propriétés, applications, calcul (exemples)

En utilisant le théorème de Pythagore pour l'espace, nous devons

D = (6² + 8² + dix²)^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Zone de cube

Comme chaque bord a la même longueur, nous avons que a = b et a = c. Remplacement dans la formule précédente, nous avons

A = 2 (aa + aa + aa) = 2 (3a²) = 6a²

A = 6A²

Exemple 2

La boîte d'une console de jeu a la forme d'un cube. Si nous voulons envelopper cette boîte avec du papier cadeau, combien de papier dépenserions-nous en sachant que la longueur des bords du cube est de 45 cm?

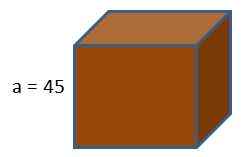
En utilisant la formule de la zone du cube, nous obtenons cela

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Zone d'un rhomboedro

Comme tous ses visages sont les mêmes, il suffit de calculer la zone de l'un d'eux et de le multiplier par six.

Nous avons que la zone d'un losange peut être calculée par ses diagonales avec la formule suivante

POUR_R = (Dd) / 2

En utilisant cette formule, il s'ensuit que la zone totale du Rhomboedro est

POUR_T = 6 (dd) / 2 = 3dd.

Exemple 3

Les visages du prochain Rhomboedro sont formés par un losange dont la diagonale est d = 7 cm et d = 4 cm. Votre région sera

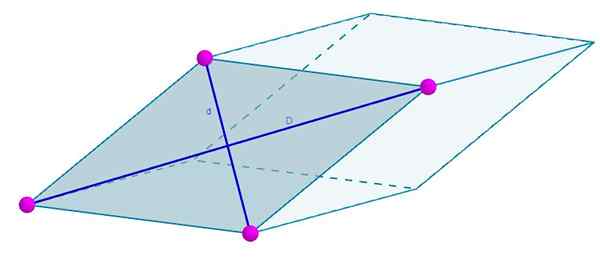
A = 3 (7 cm) (4 cm) = 84 cm².

Zone d'un rhomboedro

Pour calculer la zone d'un rhomboiedro, nous devons calculer la zone des rhomboïdes qui le composent. Alors que les parallélépipés remplissent la propriété que les côtés opposés ont la même zone, nous pouvons associer les côtés en trois pairs.

De cette façon, nous avons que votre région sera

POUR_T = 2B₁H₁ + 2B₂H₂ + 2B₃H₃

Où b_Toi sont les bases associées aux côtés et h_Toi sa hauteur relative correspondant auxdites bases.

Exemple 4

Considérez le parallèle suivant,

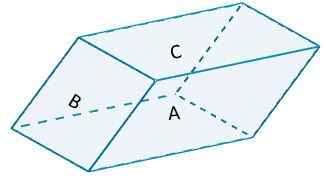
où les côté A et le côté A '(leur côté opposé) sont basés b = 10 et par hauteur h = 6. La zone marquée aura une valeur de

POUR₁ = 2 (10) (6) = 120

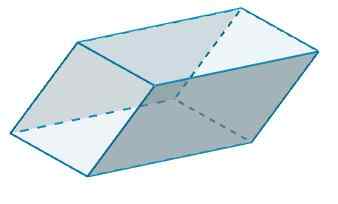
B et b 'ont b = 4 et h = 6, alors

POUR₂ = 2 (4) (6) = 48

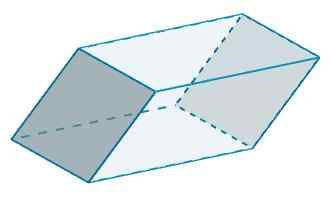
Et c et c 'ont b = 10 et h = 5, aussi

POUR₃ = 2 (10) (5) = 100

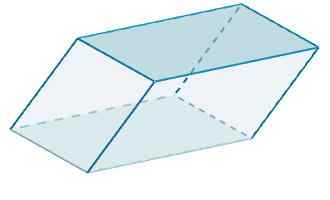
Enfin, la région de Rhomboiedro est

A = 120 + 48 + 100 = 268.

Volume d'un parallélépipant

La formule qui nous donne le volume d'un parallélépipée est le produit de la zone de l'un de ses visages en raison de la hauteur correspondant à ce visage.

V = a_CH_C

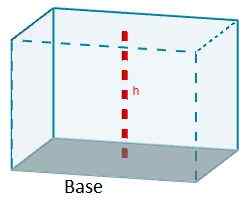
Selon le type de parallélépipé, cette formule peut être simplifiée.

Ainsi, nous avons, par exemple, que le volume d'un orthoedro serait donné par

V = abc.

Où a, b et c représentent la longueur des bords orthoedro.

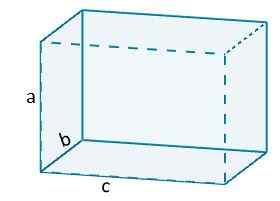
Et dans le cas particulier du cube est

V = a³

Exemple 1

Il existe trois modèles différents pour les boîtes à cookies et vous voulez.

Le premier est un cube dont le bord a une longueur de A = 10 cm.

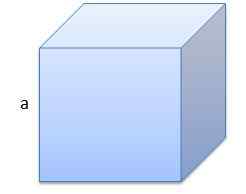
Son volume sera V = 1000 cm³

Le second est b = 17 cm, c = 5 cm, d = 9 cm.

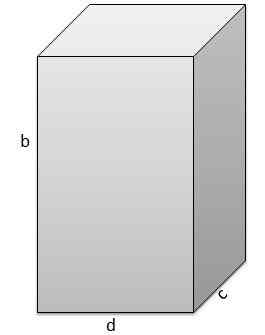
Et donc son volume est v = 765 cm³

Et le troisième a e = 9 cm, f = 9 cm et g = 13 cm.

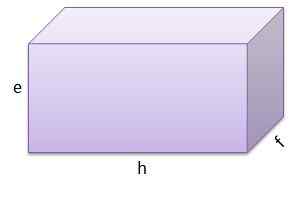
Et son volume est v = 1053 cm³

Peut vous servir: types d'angles, caractéristiques et exemples

Par conséquent, la boîte avec le plus grand volume est le troisième.

Une autre méthode pour obtenir le volume d'un parallèle est de recourir à l'algèbre vectorielle. En particulier, le produit scalaire triple.

L'une des interprétations géométriques du produit scalaire triple est celle du volume du parallélépipée, dont les bords sont trois vecteurs qui partagent le même sommet qu'un point de départ.

De cette façon, si nous avons un parallèle et nous voulons savoir quel est son volume, il suffit de le représenter dans un système de coordonnées en R³ coïncidant l'un de ses sommets avec l'origine.

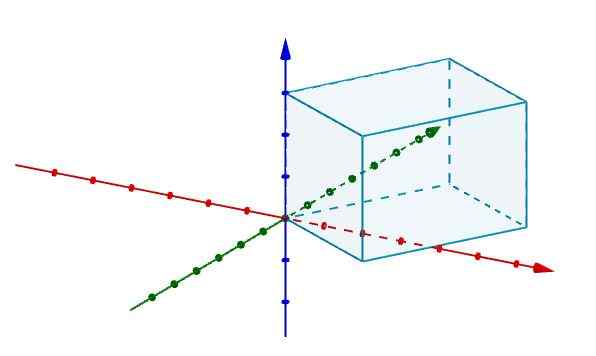
Ensuite, nous représentons les bords qui sont d'accord à l'origine avec des vecteurs, comme le montre la figure.

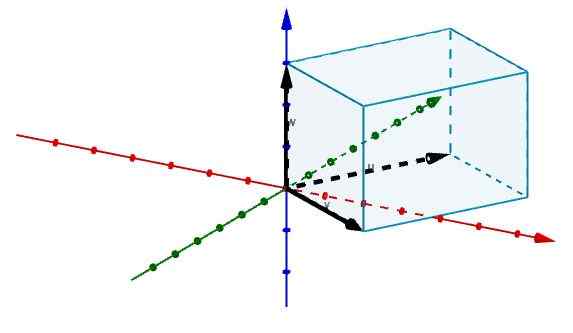
Et de cette façon, nous avons que le volume de ladite parallélépipie est donné par

V = | Axb ∙ c |

Ou équivalent, le volume est le déterminant de la matrice 3 × 3, formée par les composants des vecteurs de bord.

Exemple 2

En représentant le parallélépipé suivant en r³ Nous pouvons voir que les vecteurs qui le déterminent sont les suivants

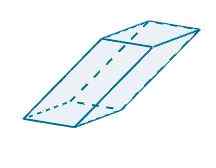
u = (-1, -3.0), v = (5, 0, 0) et w = (-0.25, -4, 4)

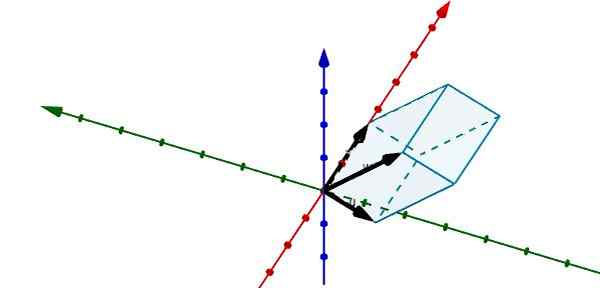
En utilisant le produit scalaire triple que nous avons

V = | (Uxv) ∙ w |

Uxv = (-1, -3.0) x (5, 0, 0) = (0,0, -15)

(Uxv) ∙ w = (0,0, - 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 (- 15) = - 60

Cela conclut que v = 60

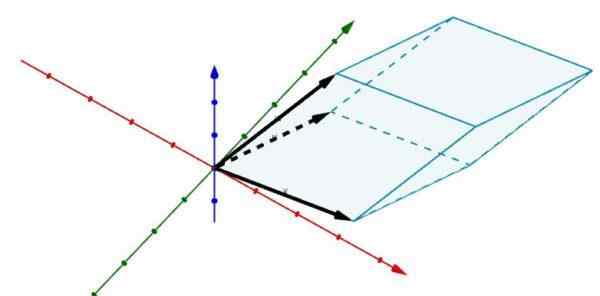
Considérez maintenant le parallélépipé suivant en R³ dont les bords sont déterminés par les vecteurs

A = (2, 5, 0), b = (6, 1, 0) et c = (3, 4, 4)

L'utilisation de déterminants nous donne que

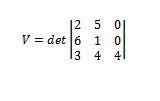
Ainsi, nous avons que le volume dudit parallélépipé est 112.

Les deux sont des moyens équivalents de calculer le volume.

Parallèle parfait

Il est connu sous le nom d'Euler Brick (ou Euler Block) à un Orthoedro qui remplit la propriété que la longueur de ses bords et la longueur des diagonales de chacun de ses visages sont des nombres entiers.

Alors qu'Euler n'a pas été le premier scientifique à étudier les orthoédeurs qui rencontrent cette propriété, il a trouvé des résultats intéressants à leur sujet.

La plus petite brique d'Euler a été découverte par Paul Halcke (1662-1731) et les longueurs de ses bords sont a = 44, b = 117 et c = 240.

Un problème ouvert dans la théorie des nombres est le suivant:

Y a-t-il des ortho-ormeurs parfaits?

À l'heure actuelle, cette question n'a toujours pas de réponse, car il n'a pas été possible de prouver qu'il n'y a pas de corps, mais personne n'a été retrouvé.

Ce qui a été démontré jusqu'à présent, c'est que le parallélépipé parfait à faire. Le premier à découvrir a la longueur de ses bords les valeurs 103, 106 et 271.

Les références

1. Guy, R. (1981). Problèmes non résolus dans la théorie des nombres. Springer.
2. Landaverde, F. d. (1997). Géométrie. Progrès.
3. Leithold, L. (1992). Le calcul avec géométrie analytique. Harla, s.POUR.
4. Rendon, un. (2004). Dessin technique: cahier d'activité 3 2e baccalauréat. Tebar.
5. Resnick, r., Halliday, D., & Krane, k. (2001). Vol Physique. 1. Mexique: Continental.