Définition paraboloïde hyperbolique, propriétés et exemples

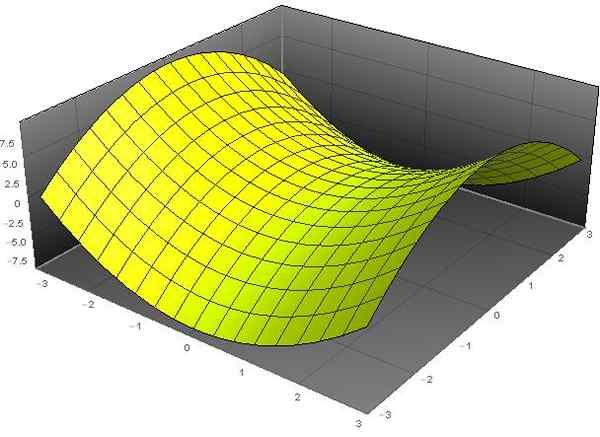
UN paraboloïde hyperbolique C'est une surface dont l'équation générale dans les coordonnées cartésiennes (x, y, z) rencontre l'équation suivante:

(pour)² - (et B)² - Z = 0.

La dénomination "paraboloïde" provient du fait que la variable Z dépend des carrés des variables X et Y. Tandis que l'adjectif "hyperbolique" est dû au fait que l'équation d'une hyperbole a une valeur fixe de z. La forme de cette surface est similaire à celle d'une chaise d'équitation.

Figure 1. Paraboloïde hyperbolique z = x² - et². Source: F. Zapata via Wolfram Mathematica.

[TOC]

Description du paraboloïde hyperbolique

Pour comprendre la nature du paraboloïde hyperbolique, l'analyse suivante sera effectuée:

1.- Le cas particulier sera pris a = 1, b = 1, c'est-à-dire que l'équation cartésienne du paraboloïde reste comme z = x² - et².

2.- Ils sont considérés comme des plans parallèles au plan ZX, c'est-à-dire y = ctte.

3.- Avec y = ctte c'est z = x² - C, qui représente les paraboles avec les branches vers le haut et le sommet sous le plan XY.

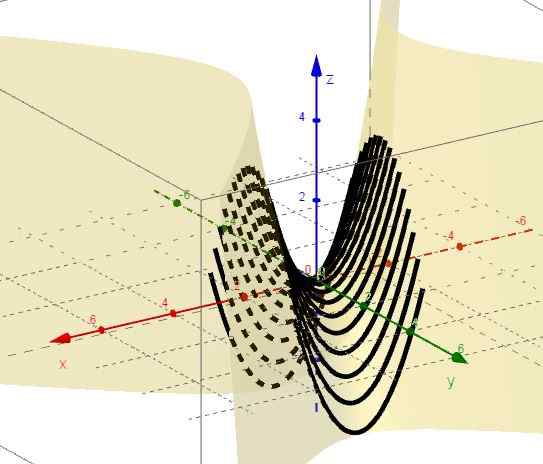Figure 2. Famille de courbes z = x² - C. Source: F. Zapata à travers Geogebra.

4.- Avec x = ctte est z = c - y², qui représente les paraboles avec les branches vers le bas et le sommet au-dessus du plan XY.

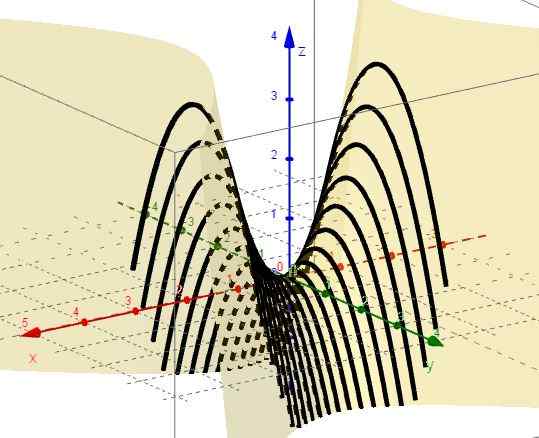figure 3. Famille de courbes z = c - et². Source: F. Zapata à travers Geogebra.

5.- Avec z = ctte est c = x² - et², qui représentent des hyperbolas dans des plans parallèles au plan XY. Lorsque c = 0, il y a deux lignes (a + 45º et -45º par rapport à l'axe x) qui sont interceptées à l'origine sur le plan xy.

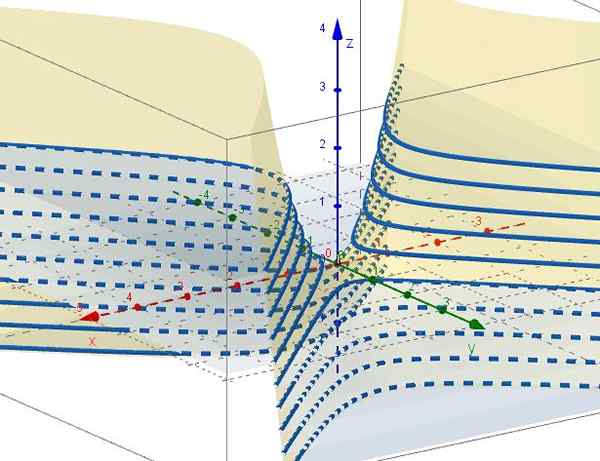Figure 4. Famille de courbes x² - et² = C. Source: F. Zapata à travers Geogebra ..

Propriétés du paraboloïde hyperbolique

1.- Quatre points différents dans l'espace à trois dimensions définissent un et seulement un paraboloïde hyperbolique.

Il peut vous servir: limiter les propriétés (avec des exemples)

2.- Le paraboloïde hyperbolique est un Surface de doublure. Cela signifie qu'en dépit d'être une surface incurvée, pour chaque point d'un paraboloïde hyperbolique, deux lignes différentes passent complètement au paraboloïde hyperbolique. L'autre surface qui n'est pas un plan et est doublement réglementée est la Hyperboloïde de la révolution.

Il s'agit précisément de la deuxième propriété du paraboloïde hyperbolique qui a permis une large utilisation de celle-ci dans l'architecture car la surface peut être générée à partir de poutres ou de cordes droites.

La deuxième propriété du paraboloïde hyperbolique en permet une définition alternative: C'est la surface qui peut être générée par une ligne mobile droite parallèle à un plan fixe et coupe deux lignes fixes qui servent de guide. La figure suivante clarifie cette définition alternative du paraboloïde hyperbolique:

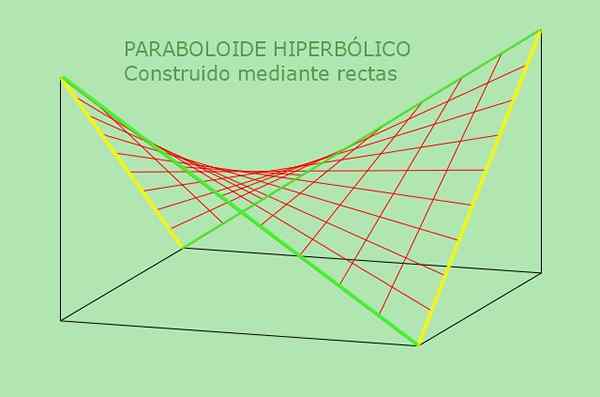Figure 5. Le paraboloïde hyperbolique est une surface doublement régulée. Source: F. Zapata.

Exemples résolus

- Exemple 1

Démontrer que l'équation: Z = xy, correspond à un paraboloïde hyperbolique.

Solution

Une transformation sera appliquée dans les variables x et y correspondant à une rotation des axes cartésiens par rapport à l'axe Z de +45. Les anciennes coordonnées X et Y sont transformées en les nouveaux X 'E et' Selon les relations suivantes:

x = x '- y'

y = x '+ et'

Bien que la coordonnée z reste la même, c'est z = z '.

En remplaçant dans l'équation z = x et nous avons:

z '= (x' - y ') (x' + y ')

Lors de l'application du produit notable de la différence par la somme égale à la différence de carrés, c'est:

Z '= x'² - et'²

qui correspond clairement à la définition initialement donnée du paraboloïde hyperbolique.

L'interception des plans parallèle à l'axe xy avec le paraboloïde hyperbolique z = x et déterminer les hyperbolas équilatéraux qui ont des asymptotes les plans x = 0 e y = 0.

Peut vous servir: milétus tel théorème

- Exemple 2

Déterminez les paramètres pour et b du paraboloïde hyperbolique qui passe par les points A (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) et D (2, -1, 32/9).

Solution

Selon ses propriétés, quatre points dans l'espace à trois dimensions déterminent un seul paraboloïde hyperbolique. L'équation générale est:

Z = (x / a)² - (et B)²

Nous remplaçons les valeurs données:

Pour le point A, vous avez 0 = (0 / a)² - (0 / b)², équation qui est satisfaite quelles que soient les valeurs des paramètres a et b.

Le point de remplacement B est obtenu:

5/9 = 1 / A² - 1 b²

Tandis que pour le point C, il reste:

32/9 = 4 / A² - 1 b²

Enfin, pour le point D, il est obtenu:

32/9 = 4 / A² - 1 b²

Qui est identique à l'équation précédente. En bref, le système d'équations doit être résolu:

5/9 = 1 / A² - 1 b²

32/9 = 4 / A² - 1 b²

La soustraction de la deuxième équation du premier est obtenue:

27/9 = 3 / A² ce qui implique que² = 1.

De même, la deuxième équation du quadruple du premier est soustraite, obtenant:

(32-20) / 9 = 4 / A² - 4 / A² -1 b² + 4 / b²

Qui est simplifié comme:

12/9 = 3 / b² ⇒ B² = 9/4.

En bref, le paraboloïde hyperbolique qui passe par les points A, B, C et D donnés a une équation cartésienne donnée par:

Z = x² - (4/9) et²

- Exemple 3

Selon les propriétés du paraboloïde hyperbolique, deux lignes qui y sont complètement contenues passent pour chaque point. Pour le cas z = x ^ 2 - y ^ 2, trouvez l'équation des deux lignes qui traversent le point P (0, 1, -1) appartenant clairement au paraboloïde hyperbolique, de sorte que tous les points de ces lignes appartiennent également à la même.

Solution

En utilisant le produit remarquable de la différence de carrés, l'équation du paraboloïde hyperbolique peut être écrite comme suit:

Peut vous servir: quadrilatère: éléments, propriétés, classification, exemples

(x + y) (x - y) = c z (1 / c)

Où c est une constante non zéro.

L'équation x + y = c z et l'équation x - y = 1 / c correspondent à deux plans avec des vecteurs normaux n= Y m=. Le produit vectoriel m x n = La direction de l'intersection de ligne des deux plans nous donne. Ensuite, l'une des lignes qui passe par le point P et appartient au paraboloïde hyperbolique a une équation paramétrique:

= + T

Pour déterminer C, nous remplaçons le point P dans l'équation x + y = c z, obtenant:

C = -1

De même, mais compte tenu des équations (x - y = k z) et (x + y = 1 / k), vous avez l'équation paramétrique de la ligne:

= + s avec k = 1.

Bref, les deux lignes:

= + t y = + s

Ils sont complètement contenus dans le paraboloïde hyperbolique z = x² - et² passer par le point (0, 1, -1).

En tant que chèque, supposons t = 1 ce qui nous donne le point (1,2, -3) sur la première ligne. Vous devez vérifier s'il est également sur le paraboloïde z = x² - et²:

-3 = 1² - 2² = 1 - 4 = -3

Ce qui confirme qu'en vigueur, il appartient à la surface du paraboloïde hyperbolique.

Le paraboloïde hyperbolique en architecture

Figure 6. Océanographique de Valence (Espagne).Source: Wikimedia Commons.

Le paraboloïde hyperbolique a été utilisé dans l'architecture par les grands architectes d'avant-garde, parmi lesquels les noms de l'architecte espagnol Antoni Gaudí (1852-1926) et très particulièrement les Espagnols, également les Espagnols Félix Candela (1910-1997) sont très particulièrement particuliers.

Vous trouverez ci-dessous quelques œuvres basées sur le paraboloïde hyperbolique:

-Chapelle de la ville de Cuernavaca (Mexique) Travail de l'architecte Félix Candela.

-L'océanographie de Valence (Espagne), également par Félix Candela.

Les références

1. Encyclopédie des mathématiques. Surface réglée. Récupéré de: Encyclopediaofmath.org
2. Llera Rubén. Paraboloïde hyperbolique. Récupéré de: Rubenllera.Wordpress.com
3. Weisstein, Eric W. «Paraboloïde hyperbolique.”De Mathworld-A Wolfram Wew Resource. Récupéré de: Mathworld.Wolfram.com
4. Wikipédia. Paraboloïde. Récupéré de: dans.Wikipédia.com
5. Wikipédia. Paraboloïde. Récupéré de: est.Wikipédia.com
6. Wikipédia. Surface réglée. Récupéré de: dans.Wikipédia.com