Théorème fondamental de la démonstration arithmétique, applications, exercices

Il Le théorème fondamental de l'arithmétique Il déclare que tout nombre naturel supérieur à 1 peut être décomposé en tant que produit de nombres premiers - en tenant certains - et cette forme est unique pour ce nombre, bien que l'ordre des facteurs puisse être différent.

N'oubliez pas qu'un nombre premier p C'est celui qui n'admet que comme des diviseurs positifs lui-même et 1. Les chiffres suivants sont des cousins: 2, 3, 5, 7, 11, 13 et ainsi de suite, car il y a infini. Le numéro 1 n'est pas considéré comme cousin, pour avoir un seul diviseur.

Figure 1. Les euclides (à gauche) ont démontré le théorème fondamental de l'arithmétique dans ses éléments de livre (350 A.C.), Et la première démonstration complète est due à Carl F. Gauss (1777-1855) (à droite). Source: Wikimedia Commons.

Pour leur part, les nombres qui ne répondent pas à ce qui précède est appelé Nombres composés, Comme 4, 6, 8, 9, 10, 12, 14 ... Prenons le numéro 10 par exemple et immédiatement nous voyons qu'il peut être décomposé comme un produit de 2 et 5:

10 = 2 × 5

2 et 5 sont, en effet, des nombres premiers. Le théorème indique que cela est possible pour n'importe quel nombre n:

Où p₁, p₂, p₃… P_r Ce sont des nombres premiers et k₁, k₂, k₃,... k_r Ce sont des nombres naturels. Afin que les nombres premiers agissent comme des briques à partir desquelles, par multiplication, les nombres naturels sont construits.

[TOC]

Démonstration du théorème fondamental de l'arithmétique

Il commence à démontrer que chaque nombre peut se décomposer dans les facteurs premiers. Être un nombre naturel n> 1, cousin ou composé.

Par exemple, si n = 2, il peut être exprimé comme: 2 = 1 × 2, qui est cousin. De la même manière, nous procédons aux numéros suivants:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Nous continuons comme ça, en décomposant tous les nombres naturels jusqu'à ce que nous atteignions le numéro N -1. Voyons si nous pouvons le faire avec le nombre qui suit: n.

Si n est cousin, nous pouvons le décomposer comme n = 1 × n, mais supposons que n est composé et a un diviseur D, logiquement moins de n:

Peut vous servir: statistiques descriptives: historique, caractéristiques, exemples, concepts

1< d < n.

Oui n / d = p₁, avec p₁ Un nombre premier, alors n est écrit comme:

n = p₁.d

Si D est cousin, il n'y a rien de plus à faire, mais si ce n'est pas le cas, il y a un nombre n₂ qui est un diviseur de d et moins que cela: n₂ < d, por lo que d podrá escribirse como el producto de n₂ Pour un autre cousin numéro P₂:

d = p₂ n₂

Qu'en remplaçant le numéro d'origine n donnerait:

n = p₁ .p₂ .n₂

Supposons maintenant n₂ Ce n'est pas non plus un nombre premier et nous l'écrivons comme le produit d'un nombre premier P₃, pour un diviseur de son₃, tel que n₃ < n₂ < n₁ < n:

n₂ = P₃.n₃ → n = p₁ p₂ p₃.n₃

 Nous répétons cette procédure un nombre fini de fois jusqu'à ce que vous obteniez:

n = p₁.p₂.p₃ … P_r

Cela signifie qu'il est possible de décomposer tous les nombres entiers de 2 au nombre n, en tant que produit de nombres premiers.

Unicité de la décomposition dans les facteurs premiers

Voyons maintenant que, à l'exception de l'ordre des facteurs, cette décomposition est unique. Supposons que vous puissiez écrire de deux manières:

n = p₁.p₂.p₃ … P_r = q_1.q₂.q₃… Q_s  (avec r ≤ s)

Bien sûr Q₁, q₂, q₃… Ce sont aussi des nombres premiers. Comme p₁ diviser à (q_1.q₂.q₃… Q_s) Alors p₁ Il est égal à l'un des "Q", peu importe Qui, nous pouvons donc dire que p₁ = q₁. Nous divisons n entre p₁ Et nous obtenons:

p₂.p₃ … P_r =_.q₂.q₃… Q_s

Nous répétons la procédure pour tout diviser entre p_r, Ensuite, nous obtenons:

1 = q_{R + 1}… Q_s

Mais il n'est pas possible de se rendre à Q_{R + 1}… Q_s = 1 Quand r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Applications

Comme nous l'avons déjà dit, les nombres premiers représentent si vous le souhaitez, les atomes des nombres, leurs composants de base. Ainsi, le théorème fondamental de l'arithmétique a de nombreuses applications, les plus évidentes: nous pouvons travailler plus facilement avec un grand nombre si nous les exprimons comme le produit de plus petits nombres.

Peut vous servir: nombres entiers

De la même manière que nous pouvons trouver le multiple commun maximum (M.c.m.) et le diviseur commun maximum (m.C.D.), Une procédure qui nous aide à faire des sommes de fractions plus facilement, à trouver des racines de grand nombre ou à fonctionner avec des radicaux, à rationaliser et à résoudre les problèmes d'application de nature très diversifiée.

De plus, les nombres premiers sont extrêmement énigmatiques. Un modèle n'est pas encore reconnu en eux et il n'est pas possible de savoir quel sera ce qui suit. Le plus grand jusqu'à ce que les temps ont été trouvés par les ordinateurs et a 24.862.048 chiffres, Bien que les nouveaux nombres premiers apparaissent moins fréquemment à chaque fois.

Nombres primo dans la nature

Les cigales, cyclés ou Chicharras vivant dans le nord-est des États-Unis émergent en cycles de 13 ou 17 ans. Les deux sont des nombres premiers.

De cette façon, les Chicharras évitent de coïncider avec les prédateurs ou les concurrents qui ont d'autres périodes de naissance, ni les différentes variétés de Chicharra se rivalisent, car elles ne coïncident pas au cours de la même année.

Figure 2. La Cicada del Este magique des États-Unis émerge tous les 13 ou 17 ans. Source: pxfuel.

Numéros primo et achats en ligne

Les numéros primo sont utilisés dans la cryptographie pour conserver les détails des cartes de crédit lorsque vous achetez des achats en ligne. De cette façon, les données que l'acheteur arrive précisément au magasin sans se perdre ou tomber dans des personnes sans scrupules.

Comme? Les données de la carte sont codées dans un nombre n qui peuvent être exprimées comme le produit de nombres premiers. Ces nombres premiers sont la clé qui révèlent les données, mais elles sont inconnues du public, elles ne peuvent être décodées que sur le Web sur lequel ils sont dirigés.

La décomposition d'un nombre en facteurs est une tâche facile si les nombres sont petits (voir les exercices résolus), mais dans ce cas, ils sont utilisés comme nombres premiers clés de 100 chiffres qui en multiplient donnent des nombres beaucoup plus importants, dont la décomposition détaillée implique un travail énorme.

Peut vous servir: estimation ponctuelle

Exercices résolus

- Exercice 1

Décomposer 1029 en facteurs premiers.

Solution

1029 est divisible par 3. Il est connu car en ajoutant vos chiffres, la somme est un multiple de 3: 1 + 0 + 2 + 9 = 12. Comme l'ordre des facteurs ne modifie pas le produit, nous pouvons commencer là-bas:

1029 3

343

1029 = 3 × 343

D'autre part 343 = 7³, ensuite:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

Et puisque 3 et 7 sont des nombres premiers, c'est la décomposition de 1029.

- Exercice 2

Facteur trinomial x² + 42x + 432.

Solution

Le trinôme est réécrit sous la forme (x + a). (x + b) Et nous devons trouver les valeurs de A et B, de sorte que:

A + b = 42; pour.B = 432

Le nombre 432 se décompose en facteurs premiers et à partir de là, il est choisi, par Tanteo, la combinaison appropriée pour les faits ajoutés à 42.

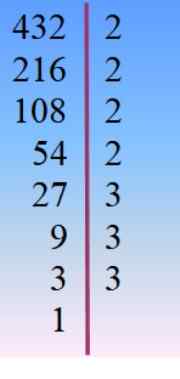
432 = 2⁴ × 3³ = 23³× 2³ = 2⁴× 3² × 3 =…

De là, il y a plusieurs possibilités d'écrire 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .

Et tout peut être trouvé en combinant des produits entre des facteurs premiers, mais pour résoudre l'exercice proposé, la seule combinaison adéquate est: 432 = 24 × 18 depuis 24 + 18 = 42, alors:

X² + 42x + 432 = (x + 24). (x +18)

Les références

1. Baldor, un. 1986. Arithmétique théorique pratique. Éditeur Cultural Company of American Textes S.POUR.
2. Monde de la BBC. Le code caché de la nature. Récupéré de: BBC.com.
3. De Leon, Manuel.Nombres primo: gardiens d'Internet. Récupéré de: blogs.20 minutes.est.
4. Unam. Théorie des nombres I: Théorème fondamental de l'arithmétique. Récupéré de: TheoriaDenumeros.Wikidot.com.
5. Wikipédia. Le théorème fondamental de l'arithmétique. Récupéré de: est.Wikipédia.org.