Papomudas

Quel est les papomudas?

Il Papomudas Il s'agit d'une procédure pour résoudre les expressions algébriques. Son acronyme indique l'ordre de priorité des opérations: parenthèses, pouvoirs, multiplication, division, addition et soustraction. En utilisant ce mot, vous pouvez facilement vous souvenir de l'ordre dans lequel une expression composée de plusieurs opérations doit être résolue.

Généralement, dans les expressions numériques, vous pouvez trouver plusieurs opérations arithmétiques ensemble, telles que les sommes, la soustraction, les multiplications et les divisions, qui peuvent également être des fractions, des pouvoirs et des racines. Pour les résoudre, il est nécessaire de suivre une procédure qui garantit que les résultats seront corrects.

Une expression arithmétique qui consiste en une combinaison de ces opérations doit être résolue en fonction de la priorité de l'ordre, également connu sous le nom de hiérarchie des opérations, établie il y a longtemps dans les conventions universelles. Ainsi, toutes les personnes peuvent suivre la même procédure et obtenir le même résultat.

Caractéristiques

Les papomudas sont une procédure standard qui établit l'ordre qui doit être suivi lorsqu'une expression doit être donnée, qui est composée d'une combinaison d'opérations telles que la somme de soustraction, la multiplication et la division.

Cette procédure établit l'ordre de priorité d'une opération par rapport aux autres à l'époque qu'ils seront; c'est-à-dire que chaque opération a un changement ou un niveau hiérarchique à résoudre.

L'ordre dans lequel les différentes opérations d'une expression doivent être résolues est donnée par chaque acronyme du mot papomudas. De cette façon, vous devez:

1. PA: parenthèses, crochets ou clés.
2. PO: pouvoirs et racines.
3. MU: Multiplications.
4. D: Divisions.
5. R: ajouts ou sommes.
6. S: soustractions ou soustraction.

Cette procédure est également appelée en anglais comme pemdas; Se souvenir facilement de ce mot est associé à la phrase: "Veuillez excuser ma chère tante Sally», Où chaque lettre initiale correspond à une opération arithmétique, de la même manière que les papomudas.

Comment les résoudre?

Sur la base de la hiérarchie établie par Papomudas pour résoudre les opérations d'une expression, il est nécessaire de réaliser l'ordre suivant:

• Premièrement, toutes les opérations qui se trouvent dans le regroupement des symboles, telles que les parenthèses, les clés, les supports et les barres de fraction doivent être résolues. Lorsqu'il y a des symboles de regroupement dans les autres, vous devriez commencer à calculer à l'intérieur.

Peut vous servir: successions quadratiques: exemples, règles et exercices résolus

Ces symboles sont utilisés pour modifier l'ordre dans lequel les opérations sont résolues, car ce qui est toujours à l'intérieur doit toujours être résolu.

• Ensuite, les pouvoirs et les racines sont résolus.
• En troisième place, les multiplications et les divisions sont résolues. Ceux-ci ont le même ordre de priorité; Par conséquent, lorsque ces deux opérations sont trouvées dans une expression, celle qui apparaît en premier doit être résolue, lisant l'expression de gauche à droite.
• En fin de compte, les sommes et la soustraction sont résolues, qui ont également le même ordre de priorité et, par conséquent, il est résolu qui apparaît d'abord dans l'expression, lu de gauche à droite.
• Les opérations ne doivent jamais être mitigées lorsqu'ils sont lus de gauche à droite, vous devez toujours suivre l'ordre de priorité ou de hiérarchie établie par les Papomudas.

Il est important de se rappeler que le résultat de chaque opération doit être placé dans le même ordre par rapport aux autres, et toutes les étapes intermédiaires doivent être séparées par un signe jusqu'à atteindre le résultat final.

Application

La procédure Papomudas est utilisée lorsque vous avez une combinaison d'opérations différentes. Compte tenu de la façon dont ils sont résolus, cela peut être appliqué dans:

Expressions contenant des sommes et des soustractions

C'est l'une des opérations les plus simples, car les deux ont le même ordre de priorité, de sorte qu'elle doit être résolue de gauche à droite dans l'expression; par exemple:

22 -15 + 8 +6 = 21.

Expressions contenant des sommes, de la soustraction et des multiplications

Dans ce cas, l'opération de priorité la plus élevée est la multiplication, alors les sommes et la soustraction sont résolues (celle qui est la première dans l'expression). Par exemple:

6 _* 4 - 10 + 8 _* 6 - 16 + 10 _* 6

= 24 -10 + 48 - 16 + 60

= 106.

Expressions contenant la somme, la multiplication de la soustraction et la division

Dans ce cas, il y a une combinaison de toutes les opérations. Il commence par résoudre la multiplication et la division qui ont une priorité supérieure, puis les sommes et la soustraction. En lisant l'expression de gauche à droite, elle est résolue en fonction de sa hiérarchie et de sa position dans l'expression; par exemple:

Peut vous servir: Mumm

7 + 10 _* 13 - 8 + 40 ÷ 2

= 7 + 130 - 8 + 20

= 149.

Expressions contenant la somme, la soustraction, la multiplication, la division et les pouvoirs

Dans ce cas, l'un des nombres est élevé à une puissance qui, dans le niveau de priorité, doit être résolu en premier, puis résoudre les multiplications et les divisions, et enfin les sommes et la soustraction:

4 + 4² _* 12 - 5 + 90 ÷ 3

= 4 + 16 _* 12 - 5 + 90 ÷ 3

= 4 + 192 - 5 + 30

= 221.

Comme les pouvoirs, les racines ont également le deuxième ordre de priorité; Par conséquent, dans les expressions qui les contiennent, ils doivent d'abord être résolus que les multiplications, les divisions, les sommes et la soustraction:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Expressions qui utilisent le regroupement des symboles

Lorsque des signes sont utilisés, tels que les parenthèses, les clés, les supports et les barres de fractions, qui se trouvent en premier, quel que soit l'ordre de priorité des opérations qu'il contient par rapport à ceux en dehors de cela, comme s'il traitait d'une séparation expression:

14 ÷ 2 - (8 - 5)

= 14 ÷ 2 - 3

= 7 - 3

= 4.

S'il y a plusieurs opérations, celles-ci doivent être résolues par ordre hiérarchique. Ensuite, les autres opérations qui composent l'expression sont résolues; par exemple:

2 + 9 * (5 + 2³ - 24 ÷ 6) - 1

= 2 + 9 * (5 + 8 - 4) - 1

= 2 + 9 * 9 - 1

= 2 + 81 - 1

= 82.

Dans certaines expressions, le regroupement des symboles dans d'autres est utilisé, par exemple lorsqu'il est nécessaire de modifier le signe d'une opération. Dans ces cas, il doit commencer par résoudre à l'intérieur; c'est-à-dire simplifier les symboles de regroupement qui sont au centre d'une expression.

Généralement, l'ordre de résoudre les opérations contenues dans ces symboles est: résoudre d'abord ce qui se trouve dans les parenthèses (), puis les supports [] et enfin les touches .

90 - 3_*[12 + (5_*4) - (4_*2)]

= 90 - 3_* [12 + 20 - 8]

Peut vous servir: probabilité théorique: comment le sortir, exemples, exercices

= 90 - 3 _* 24

= 90 - 72

= 18.

Exercices

Premier exercice

Trouvez la valeur de l'expression suivante:

vingt² + √225 - 155 + 130.

Solution

En appliquant les papomudas, les pouvoirs et les racines doivent être résolus d'abord, puis ajoute et soustraction. Dans ce cas, les deux premières opérations appartiennent au même ordre, donc celle qui est d'abord résolue, de gauche à droite:

vingt² + √225 - 155 + 130

= 400 + 15 -155 + 130.

Puis ajouter et soustraction, à partir de la gauche aussi:

400 + 15 -155 + 130

= 390.

Deuxième exercice

Trouvez la valeur de l'expression suivante:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)].

Solution

Il commence par résoudre les opérations qui se trouvent dans les parenthèses, suivant l'ordre hiérarchique qu'ils possèdent selon les Papomudas.

Les pouvoirs de la première parenthèse sont d'abord résolus, puis les opérations de la deuxième parenthèse sont résolues. Comme ils appartiennent au même ordre, la première opération de l'expression est résolue:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)]

= [- (216- 729) ÷ (8 _* 6 ÷ 16)]

= [- (216 - 729) ÷ (48 ÷ 16)]

= [- (-513) ÷ (3)].

Comme les opérations entre parenthèses ont déjà été résolues, la division qui a la plus grande hiérarchie se poursuit:

[- (-513) ÷ (3)] = [- (-171)]].

Enfin, la parenthèse qui sépare le signe moins (-) du résultat, qui dans ce cas est négatif, indique qu'une multiplication de ces signes doit être faite. Ainsi, le résultat de l'expression est:

[- (-171)] = 171.

Troisième exercice

Trouvez la valeur de l'expression suivante:

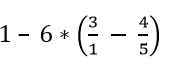
Solution

Les fractions qui se trouvent dans la parenthèse sont résolues:

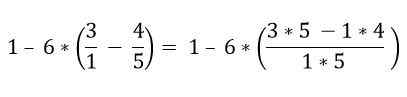
Dans la parenthèse, il existe plusieurs opérations. Les multiplications sont d'abord résolues, puis les soustractions; Dans ce cas, la barre de fraction est considérée comme un symbole de regroupement et non comme une division, de sorte que les opérations de la partie supérieure et inférieure doivent être résolues:

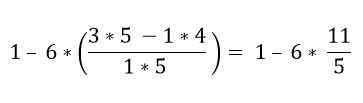
Par ordre hiérarchique, la multiplication doit être résolue:

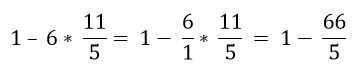
Enfin, la soustraction est résolue: