Notation décimale

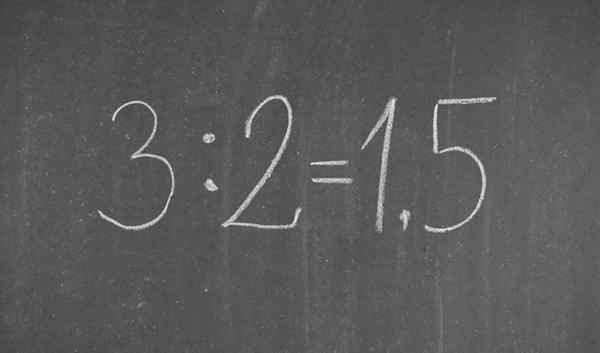La fraction 3/2 écrite en notation décimale

Qu'est-ce que la notation décimale?

La notation décimale Il consiste à écrire un nombre réel à travers une partie entière et une partie décimale, toutes deux séparées par un point ou une virgule. La partie entière est laissée et la partie décimale à droite de ce point.

Le 0 peut apparaître à la fois dans toute la partie et dans la décimale. Par exemple, les chiffres suivants sont des nombres décimaux:

• 0.25
• 1.5903
• 4 19367

Notez que la partie décimale de ces chiffres est finie, mais il y a aussi des nombres avec une partie décimale infinie, comme 0,33333…, où les points suspendus sont placés comme moyen d'indiquer que le nombre de décimales se poursuit indéfiniment indéfiniment.

En général, un nombre décimal fini peut être écrit comme:

N.pour₁pour₂pour₃… pour_n

Étant n un entier et n la quantité de décimales, tandis qu'une décimale infinie adopte la forme:

N.pour₁pour₂pour₃..

Dans la décimale 0.25 sont identifiés:

• N = 0
• pour₁ = 2
• pour₂ = 5

Les décimales surgissent comme une autre façon d'exprimer des nombres rationnels, qui sont ceux façonnés ou cassés. En fait, toute fraction peut être écrite en notation décimale, comme on le verra immédiatement.

Ils servent également à représenter des nombres qui ne dérivent pas d'une fraction, le So-appelé nombres irrationnels, comme: π, √2, √3, √5, le nombre "e" et bien d'autres.

Exemples de chiffres décimaux

Un nombre décimal peut être obtenu à partir d'une fraction de manière très simple: calculer le quotient du numérateur entre le dénominateur. Si le dénominateur est l'unité suivie de zéros, c'est très simple:

• 8/10 = 0.8
• - (5/100) = −0.05

Dans le premier cas, comme le dénominateur est de 10, le point décimal est placé immédiatement à gauche du 8 et la décimale 0.8 se lit "8 dixièmes" ou "zéro point huit".

Dans le deuxième cas, puisque le dénominateur est de 100, vous devez mettre le point décimal deux places à gauche de 5, et comme le nombre est négatif, il lit "moins 5 centièmes" ou "moins zéro point cinq".

Lorsque le dénominateur n'est pas l'unité suivie de 0, la division longue est utilisée:

Notez que pour effectuer cette division, comme le numérateur est inférieur au dénominateur, il a été multiplié d'abord par 10 et, ce faisant, un 0 suivi par le point décimal du quotient, afin de ne pas modifier l'opération, pour ne pas ne pas Pour modifier l'opération. Alors procédez normalement à diviser 10 par 2 qui est égal à 5 ​​et le résidu de division est 0.

Peut vous servir: montants vectoriels

La forme décimale de la fraction ½ est 0.5, ce «zéro point cinq» est lu:

La fraction 7/8 est un autre exemple. Comme 7 est inférieur à 8, il se multiplie 7 × 10 = 70, un 0 est placé dans le quotient suivi du point décimal et est normalement divisé:

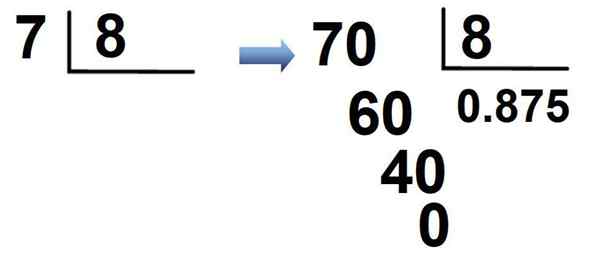
Le résultat est que la fraction est écrite en notation décimale comme:

7/8 = 0.875

Ce nombre, comme le résultat précédent, est une décimale finie et une façon de la lire est: "Zéro point huit cent soixante-quinz-de-vie". Grâce à cette procédure, les fractions suivantes sont également écrites en notation décimale:

8/10 = 0.8

5/7 = 0.714285714…

9/20 = 0.Quatre cinq

3/8 = 0.375

Notez que comme dans toutes ces fractions, le numérateur est inférieur au dénominateur, la partie entière des décimales résultantes est 0. Cependant, un nombre mixte ou un Fraction impropre (Que dont le numérateur est supérieur à son dénominateur) a également une représentation décimale.

Dans ce cas, la partie entière est supérieure ou égale à 1 si la fraction est positive et inférieure à -1 si elle est négative:

9/4 = 2.25

10/3 = 3.333333…

−12/5 = −2.4

1 ½ = 1.5

2 ¾ = 2.75

Partie entière et partie fractionnaire des décimales négatives

Dans les exemples précédents, il a été observé que pour trouver l'expression décimale d'une fraction, un numérateur et un dénominateur sont simplement divisés. Même si la fraction est négative, le signe moins le signe est mis à l'expression décimiante équivalente.

Cependant, la partie entière et la partie fractionnaire d'une décimale diffèrent en fonction du signe que vous portez.

Quand une décimale est positive, comme 2.25, sa partie entière est 2 et sa partie décimale est 0.25 et le nombre peut être écrit comme la somme de toute la partie et la partie décimale, comme ceci:

2.25 = 2 + 0.25

La partie entière est définie comme l'entier immédiatement inférieur à la décimale et la partie décimale est toujours positive. Pour 2.25, l'entier inférieur immédiatement est 2.

Mais dans le cas de la fraction −12/5, équivalent à la décimale −2.4 Ce qui précède ne fonctionne pas.

Peut vous servir: quelles sont les parties de l'avion cartésien?

 Si −2 c'était la partie entière, et 0.4 La partie décimale, en ajoutant serait obtenue:

−2 + 0.4 = −1.6 ≠ −2.4

Par conséquent, la partie entière de −2.4 ne peut pas être −2 mais l'entier immédiatement inférieur: −3. Mais dans ce cas, la partie fractionnaire ne serait pas 0.4, depuis en ajoutant:

−3 + 0.4 = −2.6 ≠ −2.4

Alors, quelle est la partie décimale du nombre négatif −2.4? Il soustrait le nombre décimal de toute sa partie et le résultat sera toujours positif:

−2.4 - (- 3) = 0.6

Enfin, il est prouvé qu'en ajoutant toute la partie et la partie fractionnaire, la décimale recherchée est obtenue:

−3 + 0.6 = −2.4

La procédure pour trouver une partie entière et une partie décimale de tout nombre, quel que soit le signe, est résumée de cette manière:

• La partie entière est l'entier immédiatement inférieur au nombre décimal.
• La partie décimale est calculée en soustrayant la décimale de toute sa partie.

Cependant, à des fins de calcul pratique, le nombre décimal -2.4 peut être décomposé comme - (2 + 0.4) = - 24/10 ou:

Comme on peut le voir, la représentation de notation décimale d'un nombre n'est pas unique.

Types de décimales

Il y a des nombres décimaux dont la partie décimale est finie ou infinie, qui est utilisée comme critère de classification:

Décimales finies ou exactes

Lorsque les décimales sont finies, comme 0.125, on dit également qu'ils sont décimales exactes.

Décimales infinies

Une décimale infinie est obtenue lorsque le résidu de la division entre le numérateur et le dénominateur n'est jamais réalisé 0.

À condition que la décimale vient du quotient entre deux entiers, cette partie décimale est périodique, c'est-à-dire qu'elle est composée d'une ou plusieurs figures qui sont répétées indéfiniment, appelées période.

Par exemple, numéro 3.333333… originaire de la fraction incorrecte 10/3, c'est une décimale périodique: la partie entière est 3, et après le point décimal, le nombre 3 est répété indéfiniment. Cela peut être symbolisé en plaçant une courbe ou un chapeau sur le nombre qui est répété:

La période peut être une figure plus grande, comme en fraction 5/7, dont la représentation en notation décimale est 0.71428571428571428… et il est écrit comme:

Peut vous servir: variation proportionnelle

Ces décimales dans lesquelles la période apparaît immédiatement après le point décimal est appelée Pure décimales périodiques. Cependant, dans cet autre:

La période, qui est de 45 ans, est précédée de deux chiffres qui ne sont plus répétés dans la partie décimale: 23. Ce chiffre est appelé période ante, Puisqu'il précède la période. Dans ce cas, c'est un Décimal des journaux mixtes.

Enfin, il y a des décimales infinies qui ne sont pas des journaux, qui ne proviennent pas du quotient entre deux nombres entiers. Comme mentionné au début, ces décimales appartiennent à l'ensemble nombres irrationnels, Comme le numéro PI, par exemple.

Exercices résolus

Exercice 1

Écrivez numériquement les chiffres décimaux suivants:

a) Point zéro quatre cent quarante-sept
b) cinq millièmes
c) deux unités et cinq centièmes
d) trois points de vingt-sept négatifs
e) un point huit cent vingt mille cinq cent soixante-trois

• Solution

a) 0.447

b) 0.005

c) 2.05

d) −3.27

e) 1.824563

Exercice 2

Classez les chiffres décimaux suivants dans des décimales exactes, des journaux purs, des journaux mixtes ou des nombres irrationnels. Dans tous les cas, indiquez la valeur de toute la partie, et s'ils sont des journaux ou des journaux mixtes, indiquent également la valeur de la période et de l'antérieur, selon le cas:

a) 0.35627

b) 1.21212121…

c) −1.32

d) 1.414213562… = √2

• Solution

a) 35627 est une décimale exacte. Sa partie entière est 0 et sa partie décimale est 0.35627.

b) 1.21212121… est un journal décimal et pur infini, la partie entière est 1 et la période est 21.

c) −1.32 est une décimale exacte et négative, dont la partie entière est −2. La partie décimale est calculée en soustrayant le numéro décimal de la partie entière:

−1.32 - (−2) = 0.68

d) L'expression décimale de √2 est infinie et non périodique, car c'est un nombre irrationnel.

C'est un journal mixte, la partie entière est 3, l'antérieur est 1 et la période est de 89.

Les références

1. Contributions pédagogiques et matériel didactique. Notation décimale. Récupéré de: Tecdigital.TEC.CA.Croisement.
2. Baldor, un. 2007. Arithmétique théorique pratique. Groupe de rédaction Patria S.POUR. de c.V.
3. Mathématiques pour les métiers. Comprendre la notation décimale. Récupéré de: OpenTextBC.CA.
4. Unam. Nombres rationnels: significations et représentations. Récupéré de: redi.Codéique.Unam.mx.