Nombres premiers caractéristiques, exemples, exercices

Les nombres premiers, Les cousins ​​absolus sont également appelés les nombres naturels qui ne sont que divisibles les uns avec les autres et 1. Dans cette catégorie, des chiffres tels que: 2, 3, 5, 7, 11, 13, 17, 19, 23 et bien d'autres viennent dans cette catégorie.

D'un autre côté, un numéro de composé est divisible par lui-même, par 1 et au moins un nombre supplémentaire. Nous avons par exemple le 12, qui est divisible par 1, 2, 4, 6 et 12. Par convention, le 1 n'est pas inclus dans la liste des nombres premiers ou dans les composés.

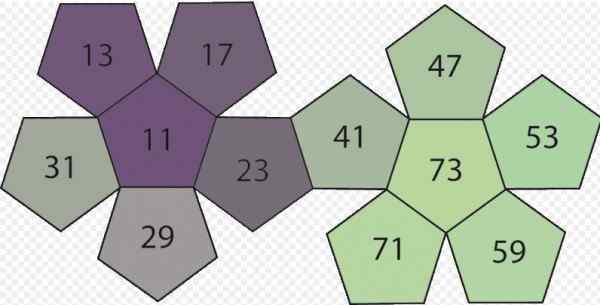
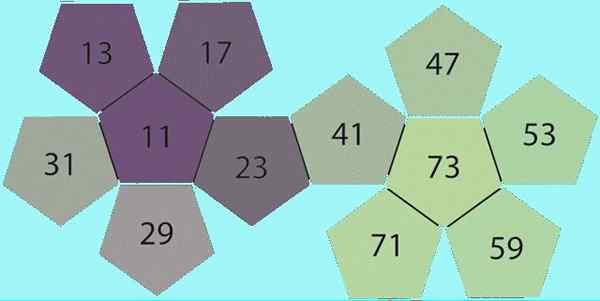Figure 1. Quelques nombres premiers. Source: Wikimedia Commons.

La connaissance des nombres premiers date des temps éloignés; Les anciens Égyptiens les ont déjà gérés et étaient sûrement connus bien avant.

Ces chiffres sont très importants, car tout nombre naturel peut être représenté par le produit de nombres premiers, étant cette représentation unique, sauf dans l'ordre des facteurs.

Ce fait est pleinement établi dans un théorème appelé Le théorème fondamental de l'arithmétique, qui indique que les nombres qui ne sont pas cousins ​​sont nécessairement constitués de produits nombres qui sont.

[TOC]

Caractéristiques des nombres premiers

Sous les principales caractéristiques des nombres premiers:

-Ils sont infinis, car un nombre important aussi important peut toujours être trouvé.

-Si un nombre premier p ne se divise pas exactement vers un autre numéro pour, On dit alors que p et pour Ce sont des cousins ​​les uns avec les autres. Lorsque cela se produit, le seul diviseur commun est 1.

Il n'est pas nécessaire de pour Être cousin absolu. Par exemple, le 5 est cousin, et bien que le 12 ne l'est pas, les deux nombres sont des cousins ​​l'un avec l'autre, car les deux ont un diviseur commun à 1.

-Quand un nombre premier p Divisez une puissance du nombre n, Il divise également un n. Considérez 100, ce qui est une puissance de 10, en particulier 10². Il arrive que les 2 divisent les 100 et 10.

-Tous les nombres premiers sont étranges à l'exception de 2, donc leur dernier chiffre est de 1, 3, 7 ou 9. Le 5 n'est pas inclus, car bien qu'il soit étrange et cousin, ce n'est jamais le chiffre final d'un autre nombre premier. En fait, tous les nombres qui se terminent en 5 sont des multiples de cela et ne sont donc pas des cousins.

Peut vous servir: Symétrie centrale: propriétés, exemples et exercices

-Ouais p C'est cousin et diviseur du produit de deux nombres pour.b, ensuite p Divisez l'un d'eux. Par exemple, le numéro de premier ordre 3 divise le produit 9 x 11 = 99, puisque 3 est un diviseur de 9.

Comment savoir si un nombre est cousin

La Primalité C'est le nom donné à la qualité d'être cousin. Eh bien, mathématique français Le petit théorème de Fermat, Cela dit:

"Compte tenu d'un numéro naturel cousin p Et tout nombre naturel pour supérieur à 0, il est réalisé que pour^p - pour C'est un multiple de p, toujours et quand p être cousin ".

Nous pouvons corroborer cela en utilisant de petits nombres, par exemple, supposons P = 4, que nous savons déjà que ce n'est pas cousin et a = 6:

6⁴ - 6 = 1296 - 6 = 1290

Le nombre 1290 n'est pas exactement divisible entre 4, donc 4 n'est pas un nombre premier.

Faisons le test maintenant avec p = 5, qui est cousin et a = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 est divisible entre 5, car tout nombre qui se termine à 0 ou 5 est. En fait 7760/5 = 1554. Comme le petit théorème de Fermat est rempli, nous pouvons nous assurer que 5 est un nombre premier.

Le test à travers le théorème est efficace et direct avec de petits nombres, dans lesquels l'opération est facile à effectuer, mais que faire s'ils nous demandent de découvrir la primalité d'un grand nombre?

Dans ce cas, le nombre est successivement divisé entre tous les nombres premiers mineurs, jusqu'à une division exacte ou que le quotient est inférieur au diviseur.

Si une division est exacte, cela signifie que le nombre est composé et si le quotient est inférieur au diviseur, cela signifie que le nombre est cousin. Nous le mettrons en pratique dans l'année résolue 2.

Façons de trouver un nombre premier

Il y a des nombres premiers infinis et il n'y a pas de formule unique pour les déterminer. Cependant, observant certains nombres premiers comme ceux-ci:

Peut vous servir: angle nul: définition et caractéristiques, exemples, exercices

3, 7, 31, 127 ..

On observe qu'ils sont dans la forme 2ⁿ - 1, avec n = 2, 3, 5, 7, 9 ... Nous vous assurons:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Mais nous ne pouvons pas s'assurer qu'en général 2ⁿ - 1 être cousin, car il y a certaines valeurs de n pour lequel cela ne fonctionne pas, par exemple sur 4:

2⁴ - 1 = 16 - 1 = 15

Et le numéro 15 n'est pas cousin, car il se termine dans 5. Cependant, l'un des plus grands nombres premiers connus, trouvés par les calculs de l'ordinateur, se trouve dans le formulaire 2ⁿ - 1 avec:

N = 57.885.161

La Formule de Mersenne nous assure que 2^p - 1 est toujours cousin, tant que p Être cousin aussi. Par exemple, le 31 est cousin, il est donc certain que 2³¹ - 1 C'est aussi:

2³¹ - 1 = 2.147.483.647

Cependant, la formule ne permet de déterminer que certains nombres premiers, pas tous.

Formule d'Euler

Le polynôme suivant permet de trouver des nombres premiers tant que N est entre 0 et 39:

P (n) = n² + N + 41

Plus tard, dans la section des exercices résolus, il y a un exemple de son utilisation.

Le dépistage des eratosténes

Eratóstenenes était un physique et un mathématique de la Grèce antique qui vivait au troisième siècle pour.C. Il a conçu une méthode graphique pour trouver les nombres premiers que nous pouvons mettre en pratique avec de petits nombres, il est appelé l'écran Eratóstenenes (un écran est comme une passoire).

-Les nombres sont placés dans une table comme celle montrée dans l'animation.

-Ensuite, les nombres pair sont étiquetés, sauf le 2 que nous connaissons est le cousin. Tous les autres en sont des multiples et donc ce ne sont pas des cousins.

-Les multiples de 3, 5, 7 et 11 sont également marqués, les excluant tous parce que nous savons que ce sont des cousins.

-Les multiples de 4, 6, 8, 9 et 10 sont déjà marqués, car ce sont des composés et donc des multiples de l'un des cousins ​​indiqués.

Peut vous servir: Histoire de la trigonométrie de ses origines

-Enfin, les chiffres restants ne sont pas marqués sont des cousins.

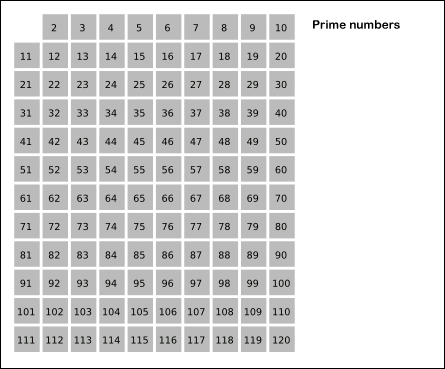Figure 2. Animation de dépistage des eratostées. Source: Wikimedia Commons.

Exercices

- Exercice 1

En utilisant le polynôme d'Euler pour les nombres premiers, trouvez 3 nombres supérieurs à 100.

Solution

C'est le polynôme qu'Euler a proposé de trouver des nombres premiers, qui fonctionnent pour n valeurs comprises entre 0 et 39.

P (n) = n² + N + 41

Grâce à Tanteo, nous sélectionnons une valeur de n, par exemple n = 8:

P (8) = 8² + 8 + 41 = 113

Comme n = 8 produit un nombre supérieur supérieur à 100, alors nous évaluons le polynôme pour n = 9 et n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Exercice 2

Découvrez si les numéros suivants sont des cousins:

a) 13

b) 191

Solution à

Le 13 est assez petit pour utiliser le petit théorème de Fermat et l'aide de la calculatrice.

Nous utilisons A = 2 pour que les nombres ne soient pas trop grands, bien qu'ils puissent également être utilisés a = 3, 4 ou 5:

2¹³ - 2 = 8190

8190 est divisible entre 2, car il est même, donc 13 est cousin. Le lecteur peut le corroborer en faisant le même test avec A = 3.

Solution B

191 est très grand pour essayer le théorème et une calculatrice commune, mais nous pouvons fourrer la division entre chaque nombre premier. Nous omettons de diviser par 2 car 191 n'est pas même et la division ne sera pas exacte ou le rapport inférieur à 2.

Nous avons essayé de diviser par 3:

191/3 = 63 666…

Et il ne donne pas exactement, ni le quotient n'est inférieur au diviseur (63 666 ... est supérieur à 3)

Nous continuons à tester 191 par les Cousins ​​5, 7, 11, 13 et la division exacte n'est pas atteinte, ni le rapport inférieur au diviseur. Jusqu'à ce qu'il divise entre 17:

191/17 = 11, 2352 ..

Comme il n'est pas exact et 11 2352 ... il est inférieur à 17, le numéro 191 est cousin.

Les références

1. Baldor, un. 1986. Arithmétique. Éditions et distributions Codex.
2. Prieto, C. Nombres primo. Récupéré de: pages.Matem.Unam.mx.
3. Propriétés des nombres premiers. Récupéré de: Mae.Ufl.Édu.
4. Smarttick. Nombres de primo: comment les trouver avec le tamis des ératostées. Récupéré de: Smartick.est.
5. Wikipédia. nombre premier. Récupéré de: est.Wikipédia.org.