Historique des nombres irrationnels, propriétés, classification, exemples

Les nombres irrationnels Ce sont ceux dont l'expression décimale a des figures infinies sans modèle répétitif, par conséquent, ils ne peuvent pas être obtenus en faisant le quotient entre deux entiers.

Parmi les nombres irrationnels les plus connus figurent:

Figure 1. De haut en bas, les numéros irrationnels suivants: Pi, le nombre d'Euler, l'Aúrea et les deux racines carrées. Source: Pixabay.

Parmi eux, sans aucun doute π (pi) est le plus familier, mais il y en a beaucoup plus. Tous appartiennent à l'ensemble des nombres réels, qui est l'ensemble numérique qui rassemble des nombres rationnels et irrationnels.

Les points suspendus de la figure 1 indiquent que les décimales suivent indéfiniment, ce qui se passe, c'est que l'espace des calculatrices actuels permet uniquement de montrer quelques-uns.

Si nous regardons attentivement, à condition que nous fassions le quotient entre deux entiers, une décimale avec des chiffres limités est obtenue ou sinon, avec des chiffres infinis sur lesquels un ou plusieurs sont répétés. Eh bien, cela ne se produit pas avec les nombres irrationnels.

[TOC]

Histoire des nombres irrationnels

Le grand mathématicien de l'Antiquité Pythagore, né en 582 de.C à Samos, en Grèce, a fondé la Pythagorean School of Thought et a découvert le célèbre théorème qui porte son nom. Nous l'avons à gauche (les Babyloniens pourraient déjà le connaître bien avant).

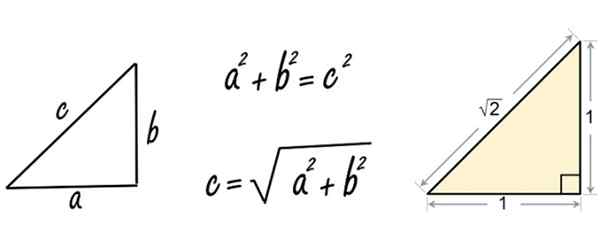Figure 2. Théorème de Pythagore appliqué à un triangle de côtés égal à 1. Source: Pixabay / Wikimedia Commons.

Eh bien, lorsque Pythagore (ou probablement un de ses disciples) a appliqué le théorème à un triangle droit de côtés égal à 1, a trouvé le nombre irrationnel √2.

Il peut vous servir: les lignes de séchage

Il l'a fait de cette façon:

C = √1² + 1² = √1 + 1 = √2

Et il a immédiatement réalisé que ce nouveau nombre ne venait pas du quotient entre deux autres nombres naturels, qui étaient ceux qui étaient connus à l'époque.

Par conséquent, il l'a appelé irrationnel, Et la découverte a provoqué une grande anxiété et confusion parmi les pythagoriciens.

Propriétés des nombres irrationnels

-L'ensemble de tous les nombres irrationnels est indiqué avec la lettre I et parfois comme q * ou q^C. L'union entre les nombres irrationnels I ou Q * et les nombres rationnels Q, donne lieu à l'ensemble des nombres N réels.

-Avec des nombres irrationnels, des opérations arithmétiques connues peuvent être effectuées: somme, soustraction, multiplication, division, potentialisation et plus.

-La division entre 0 n'est pas définie parmi les nombres irrationnels.

-La somme et le produit entre les nombres irrationnels n'est pas nécessairement un autre nombre irrationnel. Par exemple:

√2 x √8 = √16 = 4

Et 4 n'est pas un nombre irrationnel.

-Cependant, la somme d'un nombre rationnel plus irrationnel se traduit par une irrationnelle. De cette manière:

1 + √2 = 2.41421356237…

-Le produit d'un nombre rationnel différent de 0 par un nombre irrationnel est également irrationnel. Regardons cet exemple:

2 x √2 = 2.828427125…

-L'inverse d'un irrationnel se traduit par un autre nombre irrationnel. Essayons certains:

1 / √2 = 0.707106781…

1 / √3 = 0.577350269…

Ces nombres sont intéressants car ils sont également les valeurs de certaines raisons trigonométriques des angles connus. Une grande partie des raisons trigonométriques sont des nombres irrationnels, mais il y a des exceptions, comme Sen 30º = 0.5 = ½, qui est rationnel.

-Dans la somme, les propriétés commutatives et associatives sont respectées. Si A et B sont deux nombres irrationnels, cela signifie que:

Peut vous servir: fonction sur-objectif: définition, propriétés, exemples

A + b = b + a.

Et si C est un autre numéro irrationnel, alors:

(A + b) + c = a + (b + c).

-La propriété distributive de la multiplication par rapport à la somme est une autre propriété connue qui est également respectée pour les nombres irrationnels. Dans ce cas:

pour.(b + c) = a.b + a.c.

-Un irrationnel pour avoir son contraire: -a. Lorsque le résultat est ajouté, il est 0:

A + (- a) = 0

-Entre deux rationnels différents, il y a au moins un nombre irrationnel.

Emplacement d'un numéro irrationnel sur la ligne réelle

La vraie ligne est une ligne horizontale où se trouvent les nombres réels, dont les irrationnels sont une partie importante.

Pour trouver un numéro irrationnel sur la ligne réelle, sous une forme géométrique, nous pouvons valoir le théorème de Pythagore, une règle et une boussole.

À titre d'exemple, nous allons localiser √5 sur la ligne réelle, pour laquelle nous dessinons un triangle rectangle de côtés x = 2 et y = 1, Comme le montre l'image:

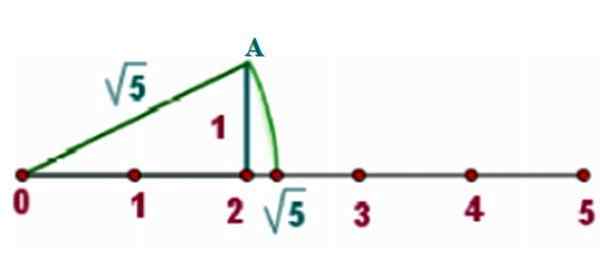figure 3. Méthode pour localiser un numéro irrationnel sur la ligne réelle. Source: F. Zapata.

Pour le théorème de Pythagore, l'hypoténuse d'un tel triangle est:

C = √2² + 1² = √4 + 1 = √5

Maintenant, le rythme avec la pointe est placé dans 0, où il y a aussi l'un des sommets du triangle droit. La pointe du crayon à boussole doit être au sommet pour.

Un arc de circonférence est dessiné qui coupe la vraie ligne. Comme la distance entre le centre de la circonférence et tout point de même est le rayon, qui vaut √5, le point d'intersection est également √5 du centre.

Du graphique, on voit que √5 est entre 2 et 2.5. Une calculatrice nous offre la valeur approximative de:

Peut vous servir: coefficient de détermination: formules, calcul, interprétation, exemples

√5 = 2.236068

Et donc, construire un triangle avec les côtés appropriés, d'autres irrationnels peuvent être localisés, comme √7 et autres.

Classification des nombres irrationnels

Les nombres irrationnels sont classés en deux groupes:

-Algébrique

-Transcendant ou transcendantal

Nombres algébriques

Les nombres algébriques, qui peuvent être irrationnels ou non, sont des solutions d'équations polynomiales dont la forme générale est:

pour_n Xⁿ + pour_N-1X^N-1 + pour_N-2X^N-2 +.. . +pour₁x + a_soit = 0

Un exemple d'équation polynomiale est une équation au deuxième degré comme celle-ci:

X³ - 2x = 0

Il est facile de démontrer que le nombre irrationnel √2 est l'une des solutions de cette équation.

Nombres transcendants

Au lieu de cela, les nombres transcendants, bien que irrationnels, ne surgissent jamais comme une solution d'une équation polynomiale.

Les nombres transcendants trouvés le plus fréquemment dans les mathématiques appliqués sont π, pour leur relation avec la circonférence et le nombre E, ou le nombre d'Euler, qui est la base des logarithmes néérians.

Exercer

Sur un carré noir, un gris est placé dans la position indiquée sur la figure. On sait que la surface du carré noir est de 64 cm². Combien coûtent les longueurs des deux carrés?

Figure 4. Deux carrés, dont la longueur des côtés est trouvée. Source: F. Zapata.

Répondre

La surface d'un carré du côté L est:

A = l²

Comme le carré noir est de 64 cm² de superficie, son côté doit être de 8 cm.

Cette mesure est la même que La diagonale du carré gris. En appliquant le théorème de Pythagore à cette diagonale et en se rappelant que les côtés d'un carré mesurent le même, nous aurons:

8² = L_g² + L_g²

Où l_g C'est le côté du carré gris.

Par conséquent: 2L_g² = 8²

Application de la racine carrée des deux côtés de l'égalité:

L_g = (8 / √2) cm

Les références

1. Carena, m. 2019. Manuel des mathématiques de préunité. Université nationale de la côte.
2. Figuera, J. 2000. Mathématiques 9e. degré. Éditions co-bo.
3. Jiménez, R. 2008. Algèbre. Prentice Hall.
4. Portail éducatif. Nombres irrationnels et leurs propriétés. Récupéré de: PortaledUcative.filet.
5. Wikipédia. Nombres irrationnels. Récupéré de: est.Wikipédia.org.