Angles opposés par le sommet (avec un exercice résolu)

Les Angles opposés par le sommet Ce sont ceux qui remplissent ce qui suit: les côtés de l'un d'eux sont les prolongements des côtés de l'autre angle. Il Théorème fondamental Parmi les angles opposés par le sommet, il dit: Deux angles opposés par le sommet ont la même mesure.

Plusieurs fois, la langue est abusée en disant que les angles opposés par le sommet sont les mêmes, ce qui n'est pas correct. Le fait que deux angles aient la même mesure ne signifie pas qu'ils sont égaux. C'est comme dire que deux enfants qui ont la même taille sont égaux.

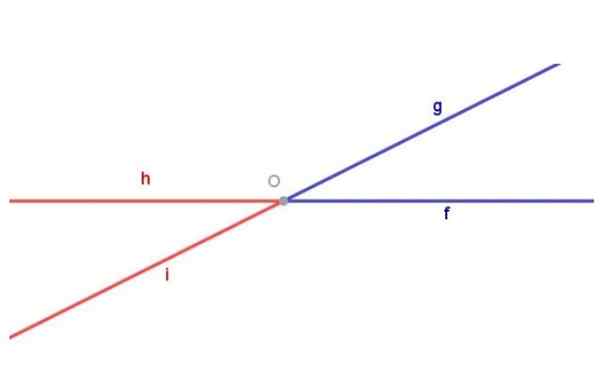
Figure 1. Angles opposés par le sommet. Préparé par: Fanny Zapata.

Rappelons qu'un angle est défini comme la figure géométrique composée de deux semi-sortants avec la même origine.

La figure 1 montre l'angle BROUILLARD (Bleu) composé de la semi-décréationnelle [De) Et le semi-sortant [OG) d'origine commune SOIT. La figure 1 montre également l'angle Hoi (rouge) composé de la semi-décréation [J'ai entendu) Et le semi-sortant [OH) les deux avec l'origine SOIT. 

Deux angles opposés par le sommet sont deux figures géométriques différentes. Pour mettre en évidence cela, dans la figure 1, l'angle a coloré BROUILLARD Bleu, tandis que l'angle Hoi Il a coloré le rouge. 

Les angles bleus et rouges de la figure 1 sont opposés au sommet parce que: le semi-droit [De) de l'angle bleu est l'allongement du semi-droit [OH) de l'angle rouge et du semi-droit [OG) de l'angle bleu est l'allongement du semi-droit [J'ai entendu) de l'angle rouge.

[TOC]

Concepts importants sur les angles

Côtés et sommets d'un angle

Le chiffre géométrique composé de deux semi-sortants avec une origine commune est un angle. L'image suivante montre l'angle Poq formé par les deux semi-droit [Op) et [OQ) d'origine commune SOIT:

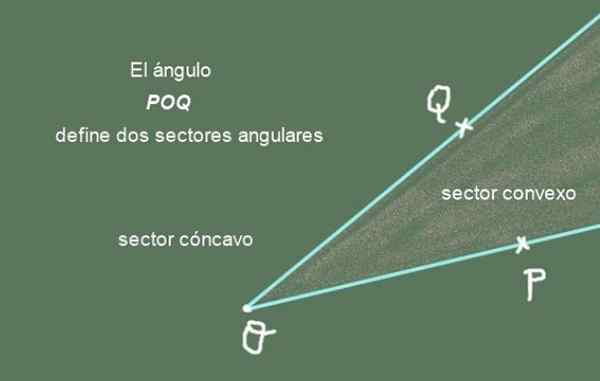Figure 2. L'angle POQ définit deux secteurs angulaires. Préparé par: f. Zapata.

Le semi -té [Op) et [OQ) sont les côtés de l'angle Poq, tandis que le point commun ou est appelé Vértice de l'angle.

Peut vous servir: règle de Sturges

Secteur angulaire: Un angle divise le plan qui le contient en deux secteurs angulaires. L'un d'eux est le secteur angulaire convexe et l'autre est le secteur angulaire concave. L'union des deux secteurs donne le plan complet.

La figure 2 montre à l'angle Poq et ses deux secteurs angulaires. Le secteur angulaire convexe est celui qui a une forme pointue, tandis que le concave est le secteur angulaire du plan manquant le secteur convexe.

Angles formés par deux lignes qui sont coupées

Deux lignes d'un plan qui sont interceptées forment quatre angles et divisent le plan en quatre secteurs angulaires.

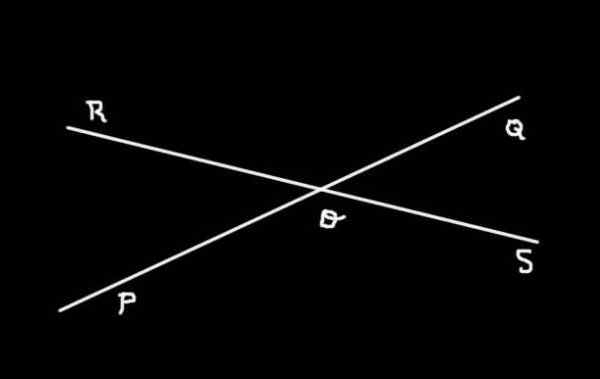figure 3. Les lignes (PQ) et (RS) sont interceptées sous O et Forms 4 angles. Préparé par: f. Zapata.

La figure 3 montre les deux lignes (Pq) et (RS) intercepté dans SOIT. Vous pouvez voir que quatre angles sont déterminés:

-Soq, Qor, Rop et Point de point

Les angles Soq et Qor, Qor et Rop, rop et Point de point, Point de point et Soq ils sont  angles adjacents entre eux, tandis que Soq et Rop Ils sont opposés par le sommet. Ils sont aussi Angles opposés par le sommet Les angles Qor et Point de point.

Lignes perpendiculaires et angle droit

Deux lignes de séchage (lignes droites se croisent) Lignes droites perpendiculaires S'ils déterminent quatre secteurs angulaires à égalité. Si chacun des quatre secteurs est symétrique avec le secteur angulaire adjacent, alors ils ont la même mesure.

Chacun des angles qui déterminent les deux lignes perpendiculaires est appelée angle droit. Tous les angles droits ont la même mesure.

Semi -té sur la même ligne et angle plat

Étant donné une ligne et un point de celui-ci, deux semi-sortants sont définis. Ces deux semi-sort-sort définissent deux angles plats.

Dans la figure 3, la ligne peut être observée (RS) Et le point SOIT qui appartient à (RS). L'angle Som C'est un angle plat. On peut également affirmer que l'angle Ros C'est un angle plat. Tous les angles plats ont la même mesure.

Peut vous servir: propriété clausurative

Angle nul et plein angle

Un seul semi-décorant définit deux angles: l'un d'eux dans le secteur angulaire convexe est le angle nul Et l'autre, celui du secteur angulaire concave est le plein angle. Dans la figure 3 le angle nul Sos et le plein angle Sos. 

La mesure 

Il existe deux systèmes numériques qui sont fréquemment utilisés pour donner la mesure d'un angle. 

L'un d'eux est le système Sexagesimal, c'est-à-dire sur la base du numéro 60. C'est un héritage des anciennes cultures mésopotamiennes. L'autre système de mesure des angles est le système radián, basé sur le nombre π (PI) et est un héritage des anciens sages grecs qui ont développé une géométrie.

Système Sexagesimal

Angle nul: Dans le système SexageSimal, l'angle nul mesure 0º (zéro degrés).

Angle complet: La mesure à 360 ° est attribuée (trois cent soixante degrés).

Angle plat: Dans le système SexageSimal, l'angle plat mesure 180 ° (cent quatre-vingts degrés).

Angle droit: Deux lignes perpendiculaires divisent le plan en quatre angles de mesure égale appelés angles droits. La mesure d'un angle droit est un quart du plein angle, soit 90 ° (quatre-vingt-dix degrés).

Convoyeur ou goniomètre

Le convoyeur est l'instrument utilisé pour mesurer les angles. Il se compose d'un demi-cercle (généralement en plastique transparent) divisé en 180 sections angulaires. À mesure qu'un demi-cercle forme un angle plat, alors la mesure entre deux sections consécutives est 1er.

Le goniomètre est similaire au transporteur et se compose d'un cercle divisé en sections angulaires à 360.

Un angle dont les côtés commencent du centre du goniomètre interceptant deux secteurs et la mesure de cet angle en degrés est égale au nombre de N de sections entre les deux secteurs interceptés, dans ce cas, la mesure sera n ° (se lit ""Degrés ENE»).

Il peut vous servir: des centimètres carrés à des mètres carrés (cm² à m²)

Théorème des angles opposés par le sommet

Formellement, le théorème est indiqué de cette manière:

Si deux angles sont opposés au sommet, alors ils ont la même mesure.

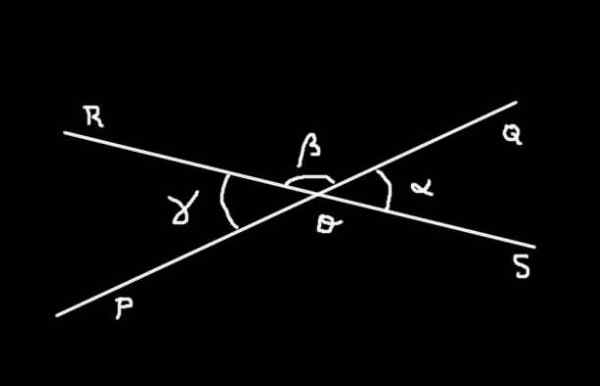Figure 4. α, β et γ sont les mesures des angles SOQ, QOR et ROP. Préparé par: f. Zapata.

Manifestation

L'angle Soq Il a une mesure α; l'angle Qor Il a une mesure β et l'angle Rop Il a une mesure γ. La somme de l'angle Soq plus lui Qor former l'angle plat Som de mesure 180º.

C'est-à-dire:

α + β = 180º

D'un autre côté et en utilisant le même raisonnement avec les angles Qor et Rop Tu as:

β + γ = 180º

Si nous observons les deux équations précédentes, la seule façon dont les deux sont remplies est que α est égal à γ.

Comme Soq Il a une mesure α et est opposé par le sommet à Rop de la mesure γ, et comme α = γ, il est conclu que les angles opposés par le sommet ont la même mesure.

Exercice résolu

En référence à la figure 4: supposons que β = 2 α. Trouver la mesure des angles Soq, Qor et Rop En degrés sexagesimaux.

Solution

Comme la somme de l'angle Soq plus lui Qor former l'angle plat Som Tu as:

α + β = 180º

Mais ils nous disent que β = 2 α. Remplacement de cette valeur de β, nous restons:

α + 2 α = 180º

C'est-à-dire:

3 α = 180º

Ce qui signifie que α est la troisième partie de 180º:

α = (180º / 3) = 60º

Alors la mesure de Soq est α = 60º. La mesure de Qor est β = 2 α = 2 * 60º = 120º. Enfin comme Rop est opposé par le sommet à Soq Ensuite, selon le théorème, il a déjà démontré qu'ils avaient la même mesure. C'est-à-dire la mesure de Rop est γ = α = 60º. 

Les références

1. Baldor, J. POUR. 1973.Géométrie plate et espace. Culturel d'Amérique centrale. 
2. Lois et formules mathématiques. Systèmes de mesure d'angle. Récupéré de: Ingecanica.com.
3. Wikipédia. Angles opposés par le sommet. Récupéré de: est.Wikipédia.com
4. Wikipédia. Convoyeur. Récupéré de: est.Wikipédia.com
5. Zapata f. Goniomètre: historique, pièces, opération. Récupéré de:.com