Échantillonnage double

Nous expliquons ce qu'est le double échantillonnage, des exemples, des avantages et des inconvénients et a mis des exercices résolus

En double échantillonnage, vous voulez en savoir plus profondément une variable d'une population

Qu'est-ce que le double échantillonnage?

Il Échantillonnage double C'est une technique qui est utilisée dans les statistiques inférentielles lorsque vous voulez en savoir plus sur une variable particulière, qui caractérise une certaine population.

Le deuxième échantillon de population est généralement effectué après un premier échantillon, dont l'analyse n'a montré aucune conclusion statistiquement significative sur aucune des variables d'étude avait été prise et analysée.

Pour cette raison, l'échantillonnage des doubles statistiques est également connu sous le nom Deux phases échantillonnage. L'utilité du deuxième échantillon réside dans lequel il aide à déterminer plus précisément l'estimation des raisons et des régressions d'une certaine variable auxiliaire, qui surgit à la lumière de l'analyse d'un premier échantillon.

Une autre utilisation qui est donnée au double échantillon est de collecter des informations pour la réalisation d'un échantillonnage de strates.

Exemples

Vous trouverez ci-dessous diverses situations dans lesquelles le double échantillonnage est justifié.

Contrôle de la qualité dans l'élaboration des pièces

La méthode d'échantillonnage double est fréquemment utilisée dans le contrôle de la qualité industrielle et se fait généralement en deux phases.

Par exemple, supposons une machine industrielle qui prépare certaines pièces. Autant que la machine est ajustée, aucune pièce n'est identique à une autre, car dans ses dimensions et son poids, de petites variations peuvent se produire. Il s'agit de déterminer si de nombreuses pièces fabriquées par cette machine répondent aux critères de tolérance afin qu'il soit accepté ou rejeté.

Tout d'abord, un échantillon aléatoire de pièces est prélevé avec lequel l'une des variables doit être vérifiée, par exemple, la longueur de la pièce, est à l'intérieur de la tolérance.

Dans le cas où la longueur moyenne est inférieure ou supérieure au degré de tolérance souhaité pour ladite variable, dans ce premier échantillon, puis il est déduit que le lot est défectueux et qu'il doit être jeté. Dans ce cas, il n'est pas nécessaire de prélever de nouveaux échantillons.

Peut vous servir: coefficient de corrélation: formules, calcul, interprétation, exemple

Au contraire, si la valeur moyenne se situe dans la plage de tolérance, mais que l'écart type de l'échantillon est suffisamment grand pour la somme ou la soustraction à la valeur moyenne est en dehors de la marge, il sera nécessaire de rassembler un deuxième échantillon majeur.

Ce deuxième échantillon doit inclure l'échantillon d'origine pour refaire les calculs et donc être en mesure de prendre une décision finale concernant la variable étudiée. De cette façon, on peut savoir si le lot est défectueux ou non.

Diminution des coûts d'échantillonnage

À plusieurs reprises, les informations sur l'une des variables que vous souhaitez étudier sont difficiles à accéder. Mais il peut y avoir une variable auxiliaire plus facilement pour la collecte de données.

Dans ce cas, deux échantillons sont prélevés, un grand pour la variable auxiliaire, moins coûteux et un échantillon mineur, contenu dans l'échantillon majeur de la variable la plus chère.

Cette méthode est applicable chaque fois qu'il est déterminé qu'il existe une corrélation entre les deux variables, qui est généralement une relation de proportionnalité.

Un exemple de cette situation apparaît dans les sciences forestières, où il est souhaité déterminer le pourcentage d'arbres touchés par une plante parasite (La Tiña).

Comme ceux-ci sont très étendus et difficiles d'accès aux régions, la population complète des arbres est irréalisable dans le temps et les coûts. Ces étapes sont ensuite suivies:

Étape 1: échantillonnage

L'échantillonnage préliminaire consisterait en l'utilisation de la photographie aérienne et la forêt est subdivisée en lot. Quelques lots sont choisis au hasard et estimés, par analyse des images des lots choisis, combien d'arbres sont affectés par la teigne, car la couleur des arbres est affectée par le parasite.

Peut vous servir: théorème d'Euclide

Étape 2: travail sur le terrain

Mais l'analyse photographique ne peut pas être précise, nous procédons donc, de préférence au hasard, quelques lots du premier échantillon à faire un travail sur le terrain.

Étape 3: Comparaison

Ensuite, le résultat du terrain est comparé à la photographie pour l'interception des deux lots. Cette comparaison peut être effectuée, par exemple, en faisant un graphique dans lequel l'axe horizontal est la valeur obtenue pour chaque lot par photographie et dans l'axe vertical la valeur obtenue par lot à travers le travail sur le terrain.

Cette méthode graphique permet d'identifier visuellement s'il existe ou non une corrélation entre les deux résultats et déterminée, par une analyse de régression, le coefficient de proportionnalité ou de rapport entre les deux échantillons.

Après l'échantillon majeur, c'est-à-dire l'échantillon photographique, la valeur moyenne des arbres infectés et son écart-type est prélevé. Mais comme le coefficient de proportionnalité et son erreur avec les échantillons de champ ont été déterminés, il est possible de corriger le résultat de l'échantillon majeur (le photographique).

Ensuite, ce résultat peut être extrapolé à la population complète d'arbres.

Avantages et inconvénients du double échantillon

Dans les exemples décrits, l'avantage du coût est la preuve.

Un inconvénient est que, dans le cas d'un double échantillonnage pour un contrôle de la qualité, il existe un risque de traverser de bons produits qui sont hors tolérance.

Exercer

Vous souhaitez estimer le nombre d'arbres malades dans une forêt de 162 hectares. Comme la forêt est très étendue, elle est subdivisée en 100 parcelles de la même zone. 18 parcelles sont choisies au hasard et grâce à une étude photographique, on estime que dans ces 18 parcelles, il y a 8 arbres malades avec une erreur standard d'environ 4,5 arbres.

Peut vous servir: quelles sont les parties de la fraction? (Exemples)

De ces 18 parcelles, 8 parcelles sont choisies au hasard. Pour ces huit parcelles, l'étude photographique se traduit par 10 arbres malades avec une erreur de plus ou moins de 5,3 arbres.

D'un autre côté, pour ces huit tracés, l'étude sur le terrain lance 12,4 arbres malades avec une erreur de plus de 6,3 arbres.

On demande:

• a) Déterminer le coefficient de proportionnalité entre l'étude sur le terrain par régression linéaire.
• b) Estimer le nombre d'arbres malades à travers la méthode photographique dans les cent parcelles.
• c) appliquer la correction avec le coefficient de proportionnalité obtenu, pour estimer le nombre réel d'arbres malades dans toute la forêt.

Solution

Un graphique du nombre d'arbres par nombre de photographies par rapport au nombre de champs pour les huit lots sélectionnés pour les deux études.

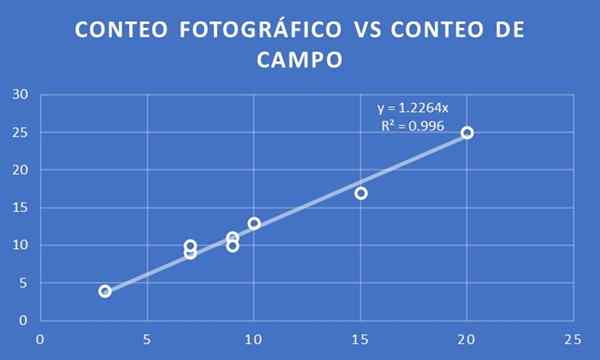Nombre photographique contre compte de champ. Source: F. Zapata.

Une ligne de tendance est ajustée et sa pente est déterminée. Dans ce cas, il est obtenu que le coefficient de proportionnalité est de 1,23. Autrement dit, si x est le nombre de comptes photographiques, on estime alors que le nombre de champs sera y = 1,23 x.

Le nombre d'arbres malades selon le nombre de photographies dans les 18 lots sélectionnés sera:

18 x 8,5 = 153

Mais comme toute la forêt a été divisée en 100 parcelles de la même zone, le nombre d'arbres malades estimés par la méthode photographique est: (100/18) x 153 = 850.

Le facteur de correction obtenu à partir de la comparaison entre le champ et l'étude photographique est maintenant appliqué:

Nombre réel estimé d'arbres malades dans la forêt = 1,23 x 850 = 1046.

Les références

1. Double échantillon pour l'estimation du ratio, Pennstate College. Récupéré du bloc d'alimentation.Édu
2. Échantillonnage double, multiple et séparé, NC State University. Récupéré de NCSU.Édu
3. Échantillonnage aléatoire simple. Récupéré d'Investopedia.com
4. Qu'est-ce que le double échantillonnage? Récupéré de: nist.Gouvernement
5. Goûter. Récupéré de: dans.Wikipédia.org
6. Échantillon à plusieurs étages. Récupéré de: dans.Wikipédia.org