Formule de fréquence accumulée, calcul, distribution, exemples

La fréquence accumulée C'est la somme des fréquences absolues f, de l'enfant à qui correspond à une certaine valeur de la variable. À son tour, la fréquence absolue est le nombre de fois qu'une observation apparaît dans l'ensemble de données.

De toute évidence, la variable d'étude doit être ordonnée. Et comme la fréquence accumulée est obtenue en ajoutant les fréquences absolues, il s'avère que la fréquence accumulée aux dernières données doit coïncider avec le nombre total d'entre eux. Sinon, il y a une erreur dans les calculs.

La fréquence accumulée est utilisée dans la gestion des données statistiques

En général, la fréquence accumulée est indiquée F_Toi (Ou parfois n_Toi), pour le distinguer de la fréquence absolue f_Toi et il est important d'ajouter une colonne pour elle dans le tableau avec lequel les données sont organisées, connues sous le nom Tableau de fréquence.

De cette façon, il est facilité, entre autres, de garder le compte du nombre de données comptées jusqu'à une certaine observation.

Un F_Toi Il est également connu sous le nom Fréquence accumulée absolue. Si vous divisez entre les données totales, vous avez le Fréquence accumulée relative, dont la somme finale doit être égale à 1.

[TOC]

Formules

La fréquence accumulée d'une certaine valeur de variable x_Toi  C'est la somme des fréquences absolues F de toutes les valeurs inférieures ou égales:

F_Toi  = F₁ + F₂ + F₃  +… F_Toi

En ajoutant toutes les fréquences absolues, le nombre total de données n est obtenu, c'est-à-dire:

F₁ + F₂ + F₃ +.. . + F_n = N

L'opération précédente est écrite de manière sommaire par le symbole de somme ∑:

∑ f_Toi = N

Autres fréquences accumulées

Les fréquences suivantes peuvent également être accumulées:

-Fréquence relative: Il est obtenu en divisant la fréquence absolue f_Toi Entre le total des données n:

F_r = F_Toi / N

Si les fréquences relatives sont ajoutées de l'enfant à celle correspondant à une certaine observation, la fréquence relative accumulée. La dernière valeur doit être égale à 1.

-Pourcentage de fréquence accumulé accumulé: La fréquence relative accumulée par 100% est multipliée.

F_% = (f_Toi / N) x 100%

Ces fréquences sont utiles pour décrire le comportement des données, par exemple en trouvant des mesures de tendance centrale.

Comment obtenir la fréquence accumulée?

Pour obtenir la fréquence accumulée, il est nécessaire de commander les données et de les organiser dans un tableau de fréquence. La procédure est illustrée dans la situation pratique suivante:

Peut vous servir: succession composée

-Dans une boutique en ligne qui vend des téléphones portables, le record des ventes d'une certaine marque du mois de mars, les valeurs suivantes par jour:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

La variable est le Nombre de téléphones vendus par jour Et c'est quantitatif. Les données présentées ne sont pas si faciles à interpréter, par exemple, les propriétaires du magasin pourraient être intéressés à savoir s'il y a une tendance, comme les jours de la semaine où les ventes de cette marque sont plus grandes.

Des informations comme celle-ci et plus encore, elles peuvent être obtenues en présentant les données de manière ordonnée et en spécifiant les fréquences.

Comment remplir le tableau de fréquence

Pour calculer la fréquence accumulée, les données sont commandées:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Ensuite, une table avec les informations suivantes est construite:

-La première colonne à gauche avec la quantité de téléphones vendus, entre 0 et 5 et dans l'ordre croissant.

-Deuxième colonne: fréquence absolue, qui est le nombre de jours qui ont été vendus 0 téléphones, 1 téléphone, 2 téléphones et ainsi de suite.

-Troisième colonne: la fréquence accumulée, composée de la somme de la fréquence précédente plus la fréquence des données à considérer.

Cette colonne commence par la première colonne de la colonne de fréquence absolue, dans ce cas, il est 0. Pour la valeur suivante, cela est ajouté avec le précédent. Ainsi, les dernières données de la fréquence accumulée se poursuivent, ce qui doit coïncider avec le total des données.

Tableau de fèche

Le tableau suivant montre la variable "Nombre de téléphones vendus en une journée", sa fréquence absolue et le calcul détaillé de sa fréquence accumulée.

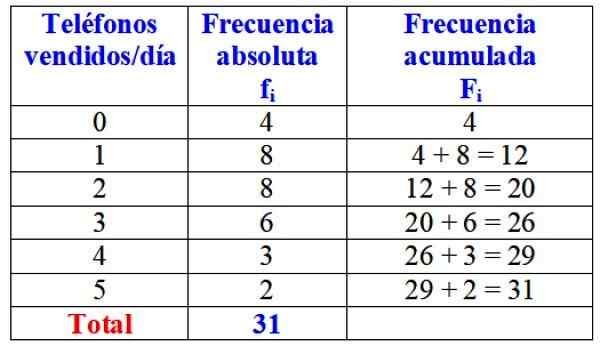Tableau des fréquences absolues et accumulées pour la variable "téléphones vendus par jour". Source: F. Zapata.

Dans un premier coup d'œil, on pourrait dire que la marque en question est presque toujours vendue un ou deux téléphones par jour, car la fréquence la plus absolue est de 8 jours, ce qui correspond à ces valeurs de la variable. Ce n'est que pour 4 jours du mois.

Il peut vous servir: Raisons trigonométriques: exemples, exercices et applications

Comme indiqué, il est plus facile d'examiner le tableau que les données lâches à l'origine.

Distribution de fréquence accumulée

Une distribution de fréquence accumulée est un tableau où les fréquences absolues, les fréquences accumulées, les fréquences relatives accumulées et les fréquences de pourcentage accumulées sont disponibles.

Bien que l'avantage d'organiser les données dans un tableau comme le précédent soit remarqué, si le numéro de données est très important, il est possible qu'il ne soit pas suffisant pour les organiser comme indiqué ci-dessus, car si de nombreuses fréquences apparaissent, il est toujours difficile interpréter.

Le problème peut être un remède en construisant un Distribution de fréquence Par intervalles, une procédure utile lorsque la variable prend un grand nombre de valeurs ou s'il s'agit d'une variable continue.

Ici, les valeurs sont regroupées en intervalles d'amplitude égale, appelés classe. Les classes sont caractérisées par le fait de:

-Limite de classe: sont les valeurs extrêmes de chaque intervalle, il y en a deux, la limite supérieure et la limite inférieure. En général, la limite supérieure n'appartient pas à l'intervalle mais à la suite immédiate, tandis que la limite inférieure appartient.

-Marque de classe: C'est le point médian de chaque intervalle et est considéré comme la valeur représentative de celui-ci.

-Largeur de classe: Il est calculé en soustrayant la valeur du major et de la plus petite (plage) et en divisant par le nombre de classes:

Classe Largeur = plage / nombre de classes

Ensuite, l'élaboration de la distribution de fréquence est détaillée.

Exemple

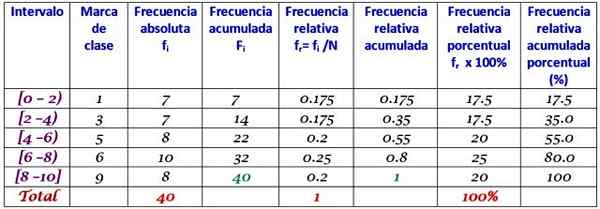
Cet ensemble de données correspond à 40 grades d'un examen de mathématiques, à l'échelle de 0 à 10:

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; dix.

Une distribution de fréquence avec une certaine quantité de classes peut être développée, par exemple 5 classes. Il convient de garder à l'esprit que lors de l'utilisation de nombreuses classes, les données ne sont pas faciles à interpréter et le sentiment d'exécution du groupe est perdu.

Peut vous servir: combien devez-vous ajouter à 3/4 pour obtenir 6/7?

Et si au contraire, ils sont regroupés en très peu, alors les informations sont diluées et une partie de celle-ci est perdue. Tout dépend de la quantité de données que vous avez.

Dans cet exemple, c'est une bonne idée d'avoir deux scores dans chaque intervalle, car il y a 10 scores et 5 classes seront créées. Le rang est la soustraction entre le major et la plus petite note, la largeur de la classe est:

Largeur de classe = (10-0) / 5 = 2

Les intervalles sont fermés par la gauche et ouverts à droite (sauf le dernier), qui est symbolisé avec des crochets et des parenthèses respectivement. Tous ont la même largeur, mais ce n'est pas obligatoire bien que le plus fréquent.

Chaque intervalle contient une certaine quantité d'éléments ou de fréquence absolue, et dans la colonne suivante se trouve la fréquence accumulée, dans laquelle la somme est transportée. Le tableau montre également la fréquence relative F_r  (fréquence absolue entre le nombre total de données) et le pourcentage de pourcentage de fréquence F_r × 100%.

Exercice proposé

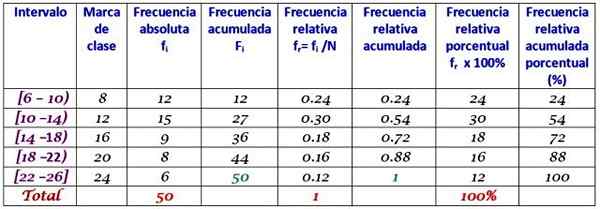
Une entreprise a passé quotidiennement ses clients au cours des deux premiers mois de l'année. Les données sont les suivantes:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 13, 17, 14, 26, 7, 12, 24, 7, 7

Groupe en 5 classes et construire le tableau avec la distribution de fréquence.

Répondre

La largeur de la classe est:

(26-6) / 5 = 4

Essayez de le résoudre avant de voir la réponse.

Les références

1. Berenson, M. 1985. Statistiques pour l'administration et l'économie. Inter-américain s.POUR.
2. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
3. Levin, R. 1988. Statistiques pour les administrateurs. 2e. Édition. Prentice Hall.
4. Probabilité et statistique. Largeur d'intervalle de classe. Récupéré de: pédroprobababilité et stadiste.Blogspot.com.
5. Spiegel, m. 2009. Statistiques. Série Schaum. 4 ta. Édition. McGraw Hill.
6. Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.