Méthode hongroise Ce qui consiste, exemple

Il Méthode hongroise Il s'agit d'un algorithme qui est utilisé dans les problèmes d'allocation lorsque vous souhaitez minimiser le coût. Autrement dit, il est utilisé pour trouver le coût minimum en attribuant plusieurs personnes à diverses activités en fonction du coût le moins élevé. Chaque activité doit être affectée à une autre personne.

Un problème d'affectation est un type spécial de problème de programmation linéaire, où l'objectif est de minimiser le coût ou le temps de terminer une quantité de travail par plusieurs personnes.

Source: Pixabay.com

L'une des caractéristiques importantes du problème d'allocation est qu'un seul travail (ou travailleur) est affecté à une machine (ou projet).

Cette méthode a été développée par le mathématicien hongrois D. Konig. Pour cette raison, il est connu comme la méthode hongroise pour les problèmes d'allocation. Il est également connu sous le nom d'algorithme d'affectation Kuhn-Munkres.

Tout problème d'allocation peut être résolu facilement en appliquant cette méthode composée de deux phases:

- Avec la première phase, il y a des réductions de lignes et de réductions de colonnes.

- Dans la deuxième phase, la solution sur une base itérative est optimisée.

[TOC]

Quelle est la méthode hongroise?

La méthode hongroise se compose de quatre étapes. Les deux premières étapes ne sont exécutées qu'une seule fois, tandis que les étapes 3 et 4 sont répétées jusqu'à ce qu'ils trouvent une affectation optimale.

Il est considéré comme un fait d'entrée sur une matrice carrée de l'ordre n par n, qui ne doit contenir que des éléments non négatifs.

Pour un problème donné, si le nombre de lignes dans la matrice n'est pas égal au nombre de colonnes, une ligne fictive ou une colonne fictive doit être ajoutée, selon l'affaire. Les coûts d'attribution de ces cellules fictives sont toujours attribués comme zéro.

Étape 1: Soustrayez les minimums de chaque ligne

Pour chaque ligne de la matrice, l'élément est sélectionné avec la valeur et les soustractions les plus basses de chaque élément de cette ligne.

Peut vous servir: quel est l'actif actuel? (Avec des exemples)

Étape 2: Soustrayez les minimums de chaque colonne

De même, l'élément avec la valeur la plus basse est sélectionné pour chaque colonne et le soustrait de chaque élément de cette colonne.

Étape 3: Couvrir tous les zéros avec un nombre minimum de lignes

Tous les zéros doivent être couverts dans la matrice résultant de l'étape 2 en utilisant un nombre minimum de lignes horizontales et verticales, soit par des lignes ou des colonnes.

Si une ligne totale est nécessaire pour couvrir tous les zéros, étant n égal à la taille n par n de la matrice, il y aura une affectation optimale entre les zéros et donc l'algorithme s'arrête.

Sinon, si moins de lignes sont nécessaires pour couvrir tous les zéros dans la matrice, cela continue avec l'étape 4.

Étape 4: Créez des zéros supplémentaires

Le moindre élément de la matrice (appelée k) est sélectionné qui n'est pas couvert par l'une des lignes réalisées à l'étape 3.

La valeur de K de tous les éléments qui ne sont pas couvertes par les lignes est soustraite. Par la suite, la valeur de k est ajoutée à tous les éléments couverts par l'intersection de deux lignes.

Les éléments couverts par une seule ligne sont laissés comme ils sont. Après avoir effectué cette étape, vous revenez à l'étape 3.

Affectation optimale

Une fois l'algorithme arrêté à l'étape 3, un ensemble de zéros est choisi de sorte que chaque ligne et chaque colonne n'ont qu'un seul zéro sélectionné.

Si dans ce processus de sélection, il n'y a pas de zéro unique dans une ligne ou une colonne, l'un de ces zéros sera alors choisi. Les zéros restants sont éliminés dans cette colonne ou cette ligne, en répétant la même chose pour les autres affectations également.

Il peut vous servir: macrolocalisation

S'il n'y a pas une seule allocation de zéros signifie qu'il existe plusieurs solutions. Cependant, le coût restera le même pour les différents ensembles d'allocations.

Toute ligne ou colonne fictive qui a été ajoutée est éliminée. Les zéros choisis dans cette matrice finale correspondent à la mission idéale requise dans la matrice d'origine.

Exemple

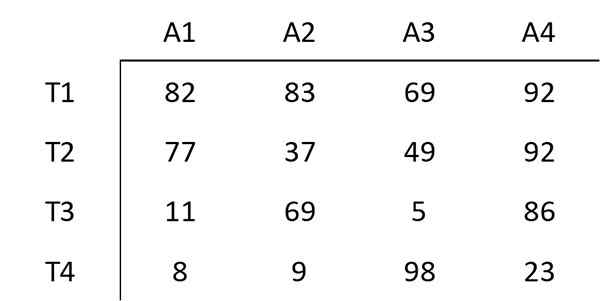
Considérez une entreprise où il y a quatre activités (A1, A2, A3, A4) qui doivent être exécutées par quatre travailleurs (T1, T2, T3, T4). Une activité par travailleur doit être affectée.

La matrice suivante montre le coût de l'attribution d'un certain travailleur à une certaine activité. L'objectif poursuivi est de minimiser le coût total de la tâche composée de ces quatre activités.

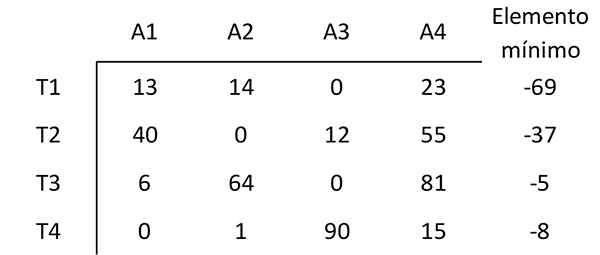
Étape 1: Soustrayez les minimums de chaque ligne

L'élément commence par la valeur minimale de chaque ligne des autres éléments de cette ligne. Par exemple, le plus petit élément de la première rangée est 69. Par conséquent, 69 de chaque élément est soustrait dans la première ligne. La matrice résultante est:

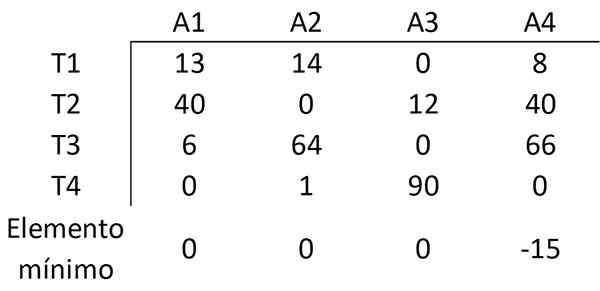
Étape 2: Soustrayez les minimums de chaque colonne

De la même manière, l'élément est soustrait avec la valeur minimale de chaque colonne des autres éléments de cette colonne, obtenant la matrice suivante:

Étape 3: Couvrir tous les zéros avec un nombre minimum de lignes

Maintenant, le nombre minimum de lignes (horizontal ou vertical) sera déterminé qui est nécessaire pour couvrir tous les zéros dans la matrice. Tous les zéros peuvent être couverts à l'aide de 3 lignes:

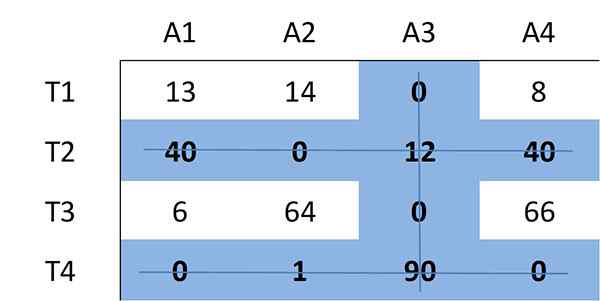
Parce que le nombre de lignes requis est de trois et est inférieure à la taille de la matrice (n = 4), elle continue avec l'étape 4.

Peut vous servir: Gestion de projet: qu'est-ce que les phases, les objectifs, les exemples

Étape 4: Créez des zéros supplémentaires

L'élément le plus bas non couvert par les lignes est sélectionné, dont la valeur est 6. Cette valeur de tous les éléments non couverts est soustraite et cette même valeur est ajoutée à tous les éléments couverts par l'intersection de deux lignes. Il en résulte la matrice suivante:

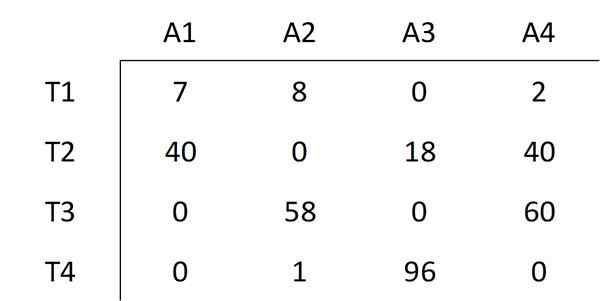
Comme indiqué dans la méthode hongroise, l'étape numéro trois doit être réalisée à nouveau.

Étape 3 (répétition)

Encore une fois, le nombre minimum de lignes nécessaires pour couvrir tous les zéros dans la matrice est déterminé. Cette fois, quatre lignes sont nécessaires:

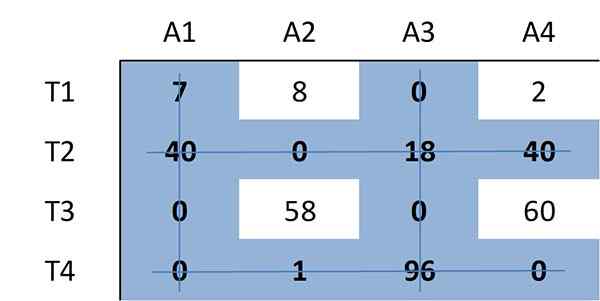
Étant donné que le nombre de lignes requis est de 4, égal à la taille de la matrice (n = 4), il existe une affectation optimale entre les zéros dans la matrice. Par conséquent, l'algorithme s'arrête.

Affectation optimale

Comme indiqué par la méthode, la sélection faite des zéros suivantes correspond à une affectation optimale:

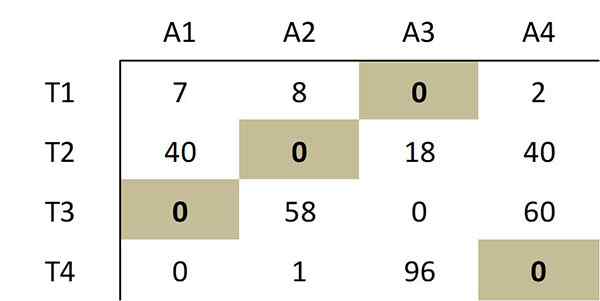
Cette sélection de zéros correspond à l'allocation optimale suivante dans la matrice de coûts d'origine:

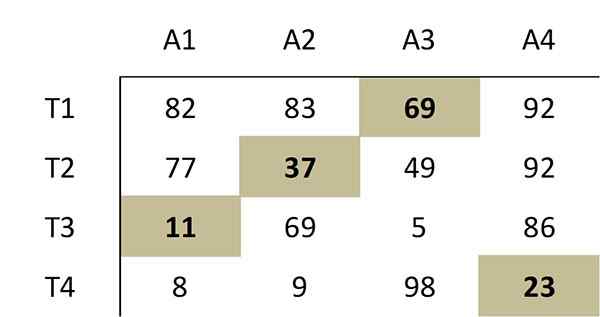
Par conséquent, le travailleur 1 doit effectuer l'activité 3, le travailleur 2, l'activité 2, le travailleur 3, l'activité 1 et le travailleur 4 doivent effectuer l'activité 4 4. Le coût total de cette affectation optimale est de 69 + 37 + 11 + 23 = 140.

Les références

1. Algorithme de Hongrie (2019). L'algorithme de Hongrie. Tiré de: Hungarianalgorithme.com.
2. Étude (2019). Utiliser l'algorithme de Hongrie pour résoudre des problèmes d'attribution. Tiré de: étudier.com.
3. Wisdom Jobs (2018). Hongrie Méthode pour résoudre le problème de l'attribution - Techniques quantitatives de gestion. Tiré de: WisdomJobs.com.
4. Geeks For Geeks (2019). Algorithme de Hongrie pour un problème d'attribution. Tiré de: geeksforgeeks.org.
5. Karleight Moore, Nathan Landman (2019). Algorithme de correspondance maximum de Hongrie. Brillant. Pris de: brillant.org.