Caractéristiques de mouvement rectiligne uniformément accélérées, formules

Il Mouvement rectiligne uniformément accéléré C'est celui qui passe sur une ligne droite et dans laquelle le mobile augmente ou diminue sa vitesse à un rythme constant. Ce taux est l'ampleur qui décrit le rythme avec lequel la vitesse change et est appelée accélération.

Dans le cas du mouvement rectiligne uniformément accéléré ou varié (MRUV), l'accélération constante est responsable du changement de l'ampleur de la vitesse. Dans d'autres types de mouvement, l'accélération est également capable de changer la direction et le sens de la vitesse, ou même changer la direction, comme dans le mouvement circulaire uniforme.

Figure 1. Les mouvements accélérés sont les plus fréquents. Source: Pixabay.

Étant donné que l'accélération représente le changement de vitesse au fil du temps, ses unités dans le système international sont M / S² (mètres en secondes au carré). Comme la vitesse, l'accélération peut être attribuée un signe positif ou négatif, à mesure que la vitesse augmente ou diminue.

Une accélération disait de +3 m / s² Cela signifie que pour chaque seconde qui passe, la vitesse mobile augmente de 3 m / s. Si au début du mouvement (à t = 0), la vitesse mobile était de +1 m / s, alors après une seconde, elle sera de 4 m / s et après 2 secondes, elle sera de 7 m / s.

Dans le mouvement rectiligne uniformément varié, les variations de vitesse que l'expérience quotidienne des objets mobiles sont prises en compte. C'est un modèle plus réaliste que celui du mouvement rectiligne uniforme. Il est toujours assez limité, car il restreint le mobile à voyager uniquement en ligne droite.

[TOC]

Caractéristiques

Ce sont les principales caractéristiques du mouvement rectiligne uniformément accéléré:

-Le mouvement passe toujours le long d'une ligne droite.

-L'accélération du mobile est constante, à la fois en ampleur et dans la direction et le sens.

-La vitesse mobile augmente (ou diminue) linéaire.

-Depuis l'accélération pour reste constant dans le temps t, Le graphique de sa magnitude en fonction du temps est une ligne droite. Dans l'exemple illustré à la figure 2, la ligne est bleue et la valeur d'accélération est lue sur l'axe vertical, environ +0.68 m / s².

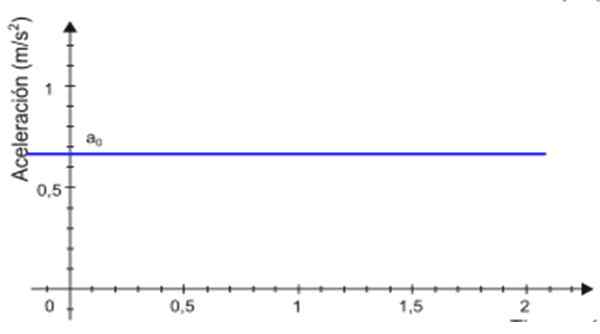Figure 2. Graphique d'accélération selon le temps d'un mouvement rectiligne uniformément varié. Source: Wikimedia Commons.

-Le graphique de vitesse V à propos t C'est une ligne droite (en vert sur la figure 3), dont la pente équivaut à l'accélération mobile. Dans l'exemple, la pente est positive.

Il peut vous servir: nitrure de bore (BN): structure, propriétés, obtention, utilisations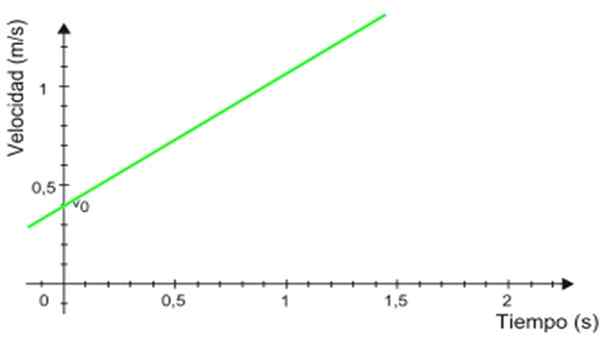 figure 3. Graphique de vitesse basé sur le temps pour un mouvement rectiligne uniformément varié. Source: Wikimedia Commons.

-La coupe avec l'axe vertical indique la vitesse initiale, dans ce cas, elle est 0.4 m / s.

-Enfin, le graphique de la position X en fonction du temps est la courbe illustrée en rouge sur la figure 4, qui est toujours une parabole.

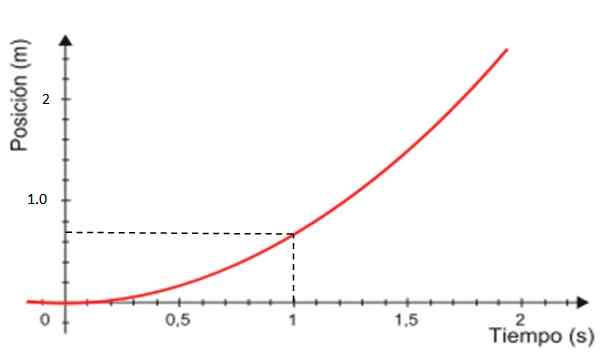Figure 4. Graphique de la position basée sur le temps pour un mouvement rectiligne uniformément varié. Source: Commons Wikimedia modifiés.

Distance parcourue du graphique V vs. t

En ayant graphique V vs. T, le calcul de la distance parcourue par le mobile est très facile. La distance parcourue est équivalente à la zone sous la ligne qui est incluse dans l'intervalle de temps souhaité.

Dans l'exemple indiqué, supposons que vous souhaitiez connaître la distance parcourue par le mobile entre 0 et 1 seconde. En utilisant ce graphique, voir la figure 5.

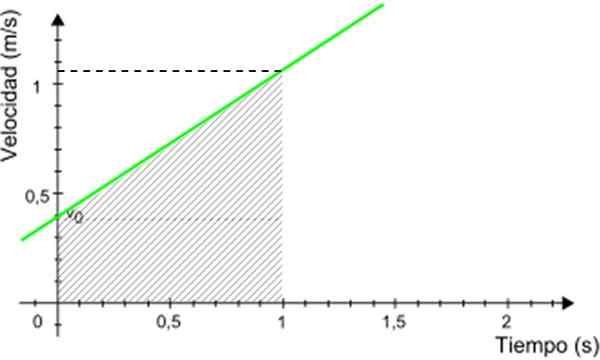Figure 5. Graphique pour calculer la distance parcourue par le mobile. Source: Commons Wikimedia modifiés.

La distance recherchait numériquement l'équivalent à la zone du trapézoïde ombré sur la figure 3. La zone trapézoïde est donnée par: (Base majeure + base mineure) x hauteur / 2

Distance parcourue = (0.4 + 1.05) x 1/2 m = 0.725 m

Il est également possible de diviser la zone ombrée en un triangle et un rectangle, de calculer les zones correspondantes et de les ajouter. La distance parcourue est positive, même si la particule va à droite ou à gauche.

Formules et équations

L'accélération moyenne et l'accélération instantanée ont la même valeur dans le MRUV, donc:

-Accélération: pour = constant

Lorsque l'accélération est égale à 0, le mouvement est rectiligne uniforme, car la vitesse serait constante dans ce cas. Le signe de pour Cela peut être positif ou négatif.

Étant donné que l'accélération est la pente de la ligne V versus t, l'équation V (T) est:

-Vitesse en fonction du temps: v (t) = v_soit + À

Où V_soit C'est la valeur de vitesse mobile initiale

-Position en fonction du temps: x (t) = x_soit + V_soit T + ½at² 

Lorsque le temps n'est pas disponible, mais au lieu de cela, il y a des vitesses et des déplacements, il y a une équation très utile qui est obtenue en dégageant le temps de v (t) = v_soit + À et le remplacer dans la dernière équation. Il s'agit de:

Peut vous servir: énergie potentielle: caractéristiques, types, calcul et exemples

-Équation qui ne contient pas de temps: V² = V_soit² +2.pour.ΔX

Exercices résolus

Lors de la résolution d'un exercice cinématique, il est important de s'assurer que la situation proposée s'adapte au modèle à utiliser. Par exemple, les équations du mouvement rectiligne uniforme ne sont pas valables pour un mouvement accéléré.

Et ceux du mouvement accéléré ne sont pas valables pour un mouvement circulaire ou curviligne, par exemple. Le premier de ces exercices résolus ci-dessous combine deux mobiles avec des mouvements différents. Pour le résoudre correctement, il est nécessaire d'aller au modèle de mouvement approprié.

-Exercice résolu 1

Pour découvrir la profondeur d'un puits, un enfant laisse tomber une pièce et active en même temps son chronomètre, qui s'arrête précisément lors de l'écoute du coup d'État de devise contre l'eau. Sa lecture était 2.5 secondes. Sachant que la vitesse du son dans l'air est de 340 m / s, calculez la profondeur du puits.

Solution

Être H La profondeur du puits. La monnaie parcourt cette distance en chute libre, un mouvement vertical uniformément varié, avec une vitesse initiale 0, car la devise est abandonnée, et une accélération constante dans la même manière que 9.8 m / s². Prendre un temps t_m En faisant cela.

Une fois que la monnaie entre en collision avec de l'eau, le son causé par le clic se rend à l'oreille de l'enfant, qui arrête le chronomètre lors de l'écoute. Il n'y a aucune raison de croire que la vitesse du son change tout en grimpant le puits, donc le mouvement sonore est uniforme rectiligne. Le son prend du temps t_s pour atteindre l'enfant.

Équation de mouvement pour la monnaie:

H = ½.g.t_m ² = 4.9 T_m ²

Où ils ont été remplacés X et pour de l'équation de la position donnée dans la section précédente, par H et g.

Équation du mouvement sonore:

H = V_s . t_s = 340 t_s

C'est l'équation familière Distance = vitesse x temps. Avec ces deux équations, il y a trois inconnues: H, TM et TS. Pour les temps, il y a une relation, on sait que tout prend 2.5 secondes pour se produire, donc:

t_m + t_s = 2.5 s

Égaliser les deux équations:

4.9 T_m ² = 340 t_s

Effacer l'un des temps et remplacer:

4.9 T_m ²= 340.(2.5 - t_m)

Lors du développement du terme des termes droits et de transformation, il est obtenu:

Peut vous servir: tir vertical: formules, équations, exemples

4.9 T_m ²+340 t_m - 850 = 0

Il s'agit d'une équation au deuxième degré avec deux solutions: 2.416 et -71.8. La solution positive est choisie, c'est celle qui a du sens, car le temps ne peut pas être négatif et en tout cas, il doit être inférieur à 2.5 secondes. Pour ce temps, il est obtenu en remplaçant la profondeur du puits:

4.9 T_m ²= 4.9 x 2.416² M = 28.6 m

-Exercice résolu 2

Une voiture voyageant à 90 km / h s'approche d'une avenue transversale avec un feu de circulation. Quand il est à 70 m, la lumière jaune est allumée, dont la durée est de 4 secondes. La distance entre le feu de circulation et le coin suivant est de 50 m.

Le conducteur a ces deux options: a) Tenez-vous à - 4 m / s² ou b) accélérer à + 2 m / s². Laquelle des deux options permet au conducteur d'arrêter ou de traverser toute l'avenue avant que la lumière ne change en rouge?

Solution

La position initiale du conducteur est x = 0 juste au moment où il voit la lumière jaune. Il est important de convertir correctement les unités: 90 km / h est égal à 25 m / s.

Selon l'option A), dans les 4 secondes que la lumière jaune dure le conducteur:

x (t) = v_soit T + ½at²= 25.4 -½.(-4).4²M = 68 m (2 mètres avant le feu de circulation)

Analyse de l'option b) Vous avez:

x (t) = v_soit T + ½at²= 25.T + ½.2.t²

Pendant que la lumière jaune dure, le conducteur voyage de cette manière:

x = 25.4 + ½.2.4²M = 116 m

Mais 116 m est inférieur à la distance disponible pour atteindre le coin suivant, qui est de 70 + 50 m = 120 m, donc il ne traverse pas toute la rue avant que la lumière rouge ne soit allumée. L'action recommandée est de s'arrêter et de rester à 2 mètres du feu de circulation.

Applications

Chaque jour, les gens éprouvent les effets de l'accélération: lorsqu'ils voyagent en voiture ou en bus, car ils doivent continuellement s'arrêter et accélérer pour adapter la marche aux obstacles de la route. L'accélération est également expérimentée lorsqu'elle monte ou baisse dans un ascenseur.

Les parcs amusants sont des sites où les gens paient pour vivre les effets de l'accélération et s'amuser.

Dans la nature, le mouvement rectiligne uniformément varié est observé lorsqu'un objet est abandonné librement, ou lorsqu'il est jeté verticalement et devrait retourner au sol. Si la résistance à l'air est méprisée, la valeur de l'accélération est celle de la gravité: 9.8 m / s2.

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.40-45.
2. Figueroa, D. Série physique pour la science et l'ingénierie. Volume 3. Édition. Cinématique. 69-85.
3. Giancoli, D.  Physique: principes avec applications. 6^e. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Sciences physiques conceptuelles. 5^e. Élégant. Pearson. 14-18.
5. Kirkpatrick, L. 2007. Physique: un regard sur le monde. 6^faire Édition abrégée. Cengage Learning. 15-19.
6. Wilson, J. 2011. Physique 10. Pearson Education. 116-119