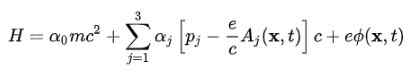Modèle aomique des caractéristiques et postulats de Dirac Jordan

Il Modèle atomique de Dirac-Jordan C'est la généralisation relativiste de l'opérateur hamiltonien dans l'équation qui décrit la fonction d'onde quantique. Contrairement au modèle précédent, celui de Schrodinger, il n'est pas nécessaire d'imposer le spin à travers le principe d'exclusion de Pauli, car il apparaît naturellement.

De plus, le modèle Dirac-Jordan intègre des corrections relativistes, une interaction spin-organe et le terme de Darwin, qui tient compte de la structure fine des niveaux électroniques de l'atome.

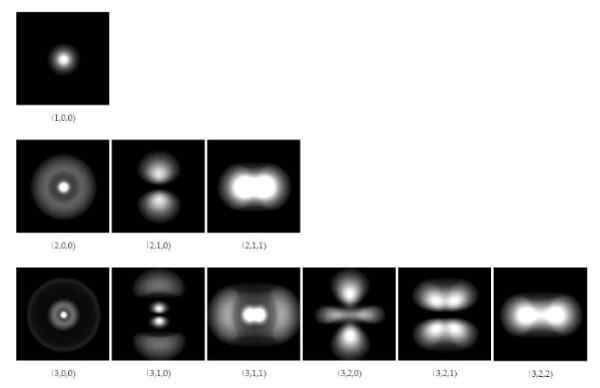
Figure 1. Orbitales électroniques dans l'atome d'hydrogène pour les trois premiers niveaux d'énergie. Source: Wikimedia Commons.

Depuis 1928, les scientifiques Paul A. M. Dirac (1902-1984) et Pascual Jordan (1902-1980), ont été proposés pour généraliser la mécanique quantique développée par Schrodinger, pour inclure les corrections de la relativité spéciale d'Einstein.

Dirac partie de l'équation de Schrodinger, qui se compose d'un opérateur différentiel, appelé Hamiltonian, qui opère sur une fonction appelée La fonction d'onde électronique. Cependant, Schrodinger n'a pas pris en compte les effets relativistes.

Les solutions de fonction d'onde permettent de calculer les régions où l'électron autour du noyau se trouve avec un certain degré de probabilité. Ces régions ou zones sont appelées Orbitales Et ils dépendent de certains nombres quantiques discrets, qui définissent l'énergie et le moment angulaire de l'électron. 

[TOC]

Postule

Dans les théories mécaniques quantiques, que ce soit relativiste ou non, il n'y a pas de concept d'orbits, car ni la position ni la vitesse de l'électron ne peuvent être spécifiées simultanément. Et en plus, la spécification de l'une des variables entraîne une imprécision totale dans l'autre.

Pour sa part, Hamiltonian est un opérateur mathématique qui agit sur la fonction d'onde quantique et est construit à partir d'énergie électronique. Par exemple, un électron libre a une énergie totale et cela dépend de son élan linéaire p de cette façon:

E = (p²) / 2m

Pour construire le hamiltonien, il commence à partir de cette expression et est remplacé p Par l'opérateur quantique pour l'élan: 

p = -I ħ ∂ / ∂r 

Il est important de noter que les termes p et p Ils sont différents, car le premier est l'élan et l'autre est le Opérateur différentiel associé à l'élan. 

Peut vous servir: Modèle atomique de Leukipo: postulats, limitations, importance

De plus, I est l'unité imaginaire et ħ la constante de Planck divisée par 2π, de cette manière l'opérateur hamiltonien h de l'électron libre est obtenu:

H = (ħ²/ 2m) ∂² / ∂r² 

Pour trouver l'hamiltonien de l'électron dans l'atome, l'interaction électronique avec le noyau est ajoutée: 

H = (ħ2 / 2m) ∂² / ∂r²  - Eφ (r)

Dans l'expression précédente -e est la charge électrique électronique et φ (r) le potentiel électrostatique produit par le noyau central.

Maintenant, l'opérateur H agit sur la fonction d'onde ψ selon l'équation de Schrodinger, qui est écrite comme celle-ci:

H ψ = (i ħ ∂ / ∂t) ψ

Les quatre postulats de Dirac

Premier postulat: L'équation des ondes relativistes a la même structure que l'équation des ondes de Schrodinger, ce qui change est H:

H ψ = (i ħ ∂ / ∂t) ψ

Deuxième postulat: L'opérateur hamiltonien est construit sur la base de la relation énergétique d'Einstein, qui est écrite comme celle-ci:

E = (m² c⁴ + p² c²)^1/2

Dans la relation précédente, si la particule a une élan p = 0, vous avez la célèbre équation e = mc² qui relie l'énergie de repos de toute masse de masse m avec la vitesse de la lumière c.

Troisième postulat: Pour obtenir l'opérateur hamiltonien, la même règle de quantification utilisée dans l'équation de Schrodinger est utilisée:

p = -I ħ ∂ / ∂r

Au début, il ne savait pas comment gérer cet opérateur différentiel agissant dans une racine carrée, alors Dirac s'est mis à obtenir un opérateur hamiltonien linéaire dans l'opérateur de momentum et est apparu son quatrième postulat.

Chambre postulante: Pour se débarrasser de la racine carrée dans la formule d'énergie relativiste, Dirac a proposé la structure suivante pour E²:

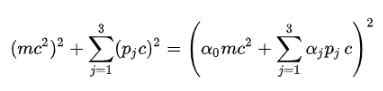
Bien sûr, il est nécessaire de déterminer les coefficients alpha (α0, α1, α2, α3) afin que cela soit rempli.

L'équation Dirac

L'équation Dirac a d'abord été soulevée pour l'électron libre, en utilisant la structure proposée dans le quatrième postulat. Il reste comme suit: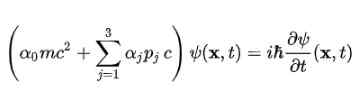

Il peut vous servir: entendre la force: surface et forces de masse

Dans sa forme compacte, l'équation de Dirac est considérée comme l'une des plus belles équations mathématiques au monde:

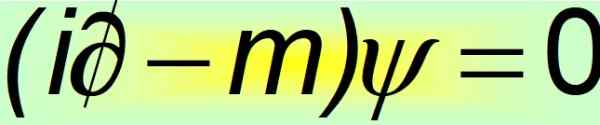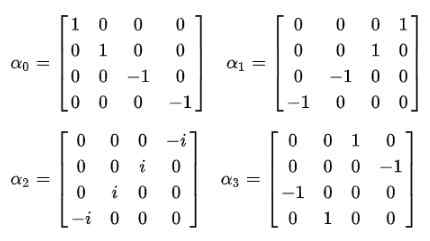
Figure 2. Équation Dirac Compact. Source: F. Zapata.

Et c'est à ce moment-là qu'il est évident que les Alfas constants ne peuvent pas être des quantités scalaires. La seule façon dont l'égalité du quatrième postulat est remplie est qu'ils sont des matrices constantes 4 × 4, qui sont appelées Matrices de dirac:

Il est immédiatement observé que la fonction d'onde cesse d'être une fonction scalaire et devient un vecteur à quatre compartiments Expinure:

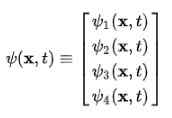
L'atome de Dirac-Jordan

Pour obtenir le modèle atomique, il est nécessaire de passer de l'équation d'électrons libre à celui de l'électron dans le champ électromagnétique produit par le noyau atomique. Cette interaction est prise en compte en incorporant le scalaire potentiel φ et le vecteur potentiel POUR Dans le hamiltonien:

La fonction d'onde (Espinor) qui résulte de l'incorporation de cet hamiltonien a les caractéristiques suivantes: 

- Il remplit la relativité spéciale, car elle prend en compte l'énergie intrinsèque de l'électron (premier mandat du hamiltonien relativiste)

- Il a quatre solutions correspondant aux quatre composantes de l'espinor

- Les deux premières solutions correspondent à une pour tourner + ½ et l'autre à la rotation - ½ 

- Enfin, les deux autres solutions prédisent l'existence de l'antimatière, car elles correspondent à celles des positrons des opposés opposés.

Le grand avantage de l'équation de Dirac est que les corrections hamiltoniennes de base de Schrodinger H (O) peuvent être décomposées en plusieurs termes que nous montrerons ci-dessous:

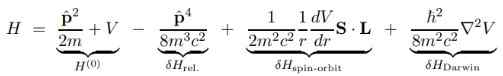
Dans l'expression précédente, V est le scalaire potentiel, car le vecteur potentiel POUR Il est vide s'il est censé au proton stationnaire central et c'est pourquoi il n'apparaît pas.

La raison pour laquelle les corrections de Dirac concernant les solutions de Schrodinger dans la fonction d'onde sont subtiles. Ils découlent du fait que les trois derniers termes de l'hamiltonien corrigé sont tous divisés par la vitesse C du carré, un immense nombre, ce qui rend ces termes numériquement petits.

Il peut vous servir: Vy Canis Majalis: découverte, caractéristiques, structure, formation et évolution

Corrections relativistes au spectre d'énergie

À l'aide de l'équation dic-jordaine, des corrections se trouvent dans le spectre d'énergie électronique dans l'atome d'hydrogène. Il existe également des corrections d'énergie dans les atomes avec plus d'un électron approximativement à travers une méthodologie connue sous le nom de théorie des perturbations.

De même, le modèle DIRAC vous permet de trouver la correction de la structure fine aux niveaux d'énergie de l'hydrogène. 

Cependant, des corrections encore plus subtiles telles que la structure hyperfine et le décalage de l'agneau sont obtenues à partir de modèles plus avancés tels que Théorie quantique de Campos, né précisément en raison des contributions du modèle Dirac.

La figure suivante montre comment les corrections relativistes de Dirac sont à des niveaux d'énergie:

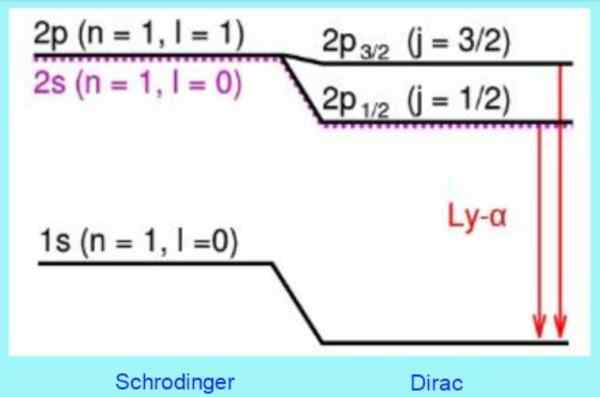figure 3. Corrections du modèle Dirac aux niveaux d'atomes d'hydrogène. Source: Wikimedia Commons.

Par exemple, les solutions à l'équation Dirac prédisent correctement un changement observé au niveau 2S. C'est la correction de structure fine bien connue dans la ligne Lyman - Alfa du spectre d'hydrogène (voir figure 3).

Soit dit en passant, la structure fine est le nom qui reçoit en physique atomique le déploiement des lignes du spectre d'émission des atomes, qui est une conséquence directe du spin électronique.

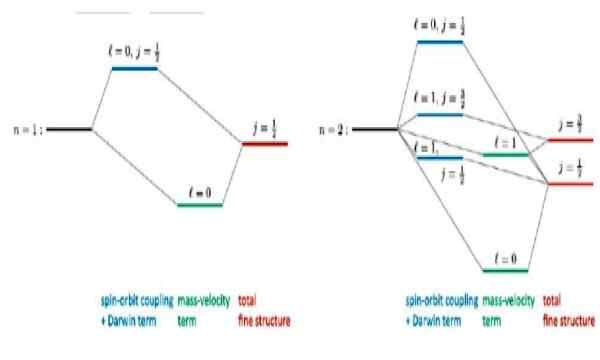Figure 4. Structure fine se dépliant pour l'état de base n = 1 et le premier état excité n = 2 dans l'atome d'hydrogène. Source: R Wirnata. Corrections relativistes aux atomes de type hydrogène. Researchgate.filet

Articles d'intérêt

Modèle atomique broglie.

Modèle atomique de Chadwick.

Modèle atomique Heisenberg.

Modèle atomique perrin.

Modèle atomique Thomson.

Modèle atomique de Dalton.

Modèle atomique Schrödinger.

Modèle atomique démocrite.

Modèle atomique de leucipo.

Modèle atomique bohr.

Modèle atomique actuel.

Les références

1. Théorie atomique. Récupéré de Wikipedia.org.
2. Moment magnétique électronique. Récupéré de Wikipedia.org.
3. Quanta: un manuel de concepts. (1974). Oxford University Press. Récupéré de Wikipedia.org.
4. Modèle atomique de Dirac Jordan. Récupéré de prezi.com.
5. Le nouvel univers quantique. la presse de l'Universite de Cambridge. Récupéré de Wikipedia.org.