Moindres carrés

Quelle est la méthode des carrés minimaux?

La méthode de Moindres carrés C'est l'une des applications les plus importantes de l'approche des fonctions. L'idée est de trouver une courbe telle que, compte tenu d'un ensemble de paires bien rangées, cette fonction est mieux approchée des données. La fonction peut être une ligne, une courbe quadratique, un cubique, etc.

L'idée de la méthode est de minimiser la somme des carrés des différences dans les ordonnées (composant Y), entre les points générés par la fonction choisie et les points appartenant à l'ensemble de données.

Méthode carrée minimale

Avant de donner la méthode, nous devons d'abord être clairs sur ce que "il approche mieux". Supposons qu'une ligne soit recherchée y = b + mx qui est celle qui représente le mieux un ensemble de n points, à savoir (x1, y1), (x2, y2)…, (xn, yn).

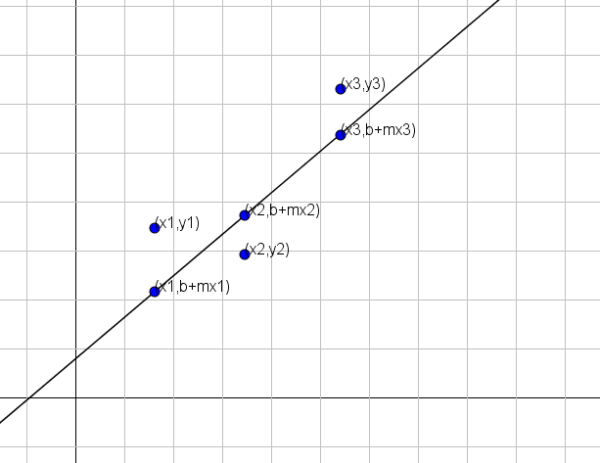
Comme le montre la figure précédente, si les variables X et Y étaient liées par la ligne y = b + mx, alors pour x = x1, la valeur correspondante de y serait b + mx1. Cependant, cette valeur est différente de la vraie valeur de y, qui est y = y1.

N'oubliez pas que dans l'avion, la distance entre deux points est donnée par la formule suivante:

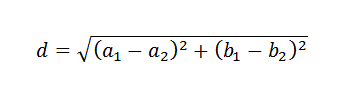
Dans cet esprit, pour déterminer comment choisir la ligne y = b + mx qui approche le mieux les données données, il semble logique à utiliser comme critère la sélection de la ligne qui minimise la somme des carrés des distances entre les points et la ligne.

Comme la distance entre les points (x1, y1) et (x1, b + mx1) est y1- (b + mx1), notre problème est réduit à la recherche de nombres m et b tel que la somme suivante est minime:

Peut vous servir: théorème vert, démonstration, applications et exercices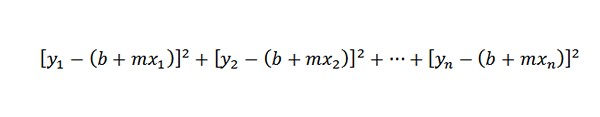

La ligne qui répond à cette condition est connue comme "l'approche de la ligne de carrés minimum aux points (x1, y1), (x2, y2), ..., (xn, yn)".

Une fois le problème obtenu, il ne reste que de choisir une méthode pour trouver l'approche par des carrés minimaux. Si les points (x1, y1), (x2, y2), ..., (xn, yn) sont tous sur la ligne y = mx + b, il faudrait être colinéaire et:

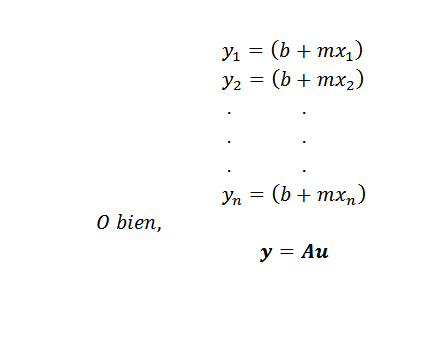
Dans cette expression:

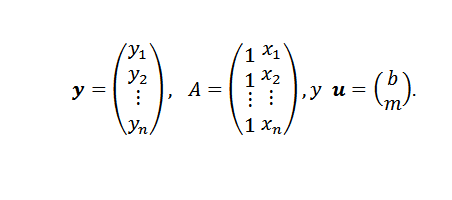
Enfin, si les points ne sont pas colinéaires, alors y-au = 0 et que le problème peut se traduire par la recherche d'un vecteur ou de telle sorte que la norme euclidienne est minime.

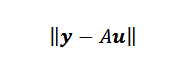
Trouver le vecteur minimisant ou n'est pas aussi difficile que vous pourriez le penser. Comme a est une matrice NX2 et U est une matrice 2 × 1, nous avons que le vecteur Au est un vecteur en Rⁿ et appartient à l'image de A, qui est un sous-espace de Rⁿ Avec une dimension pas plus de deux.

Nous supposerons que n = 3 pour montrer quelle est la procédure à suivre. Si n = 3, l'image de A sera un avion ou une ligne qui passe par l'origine.

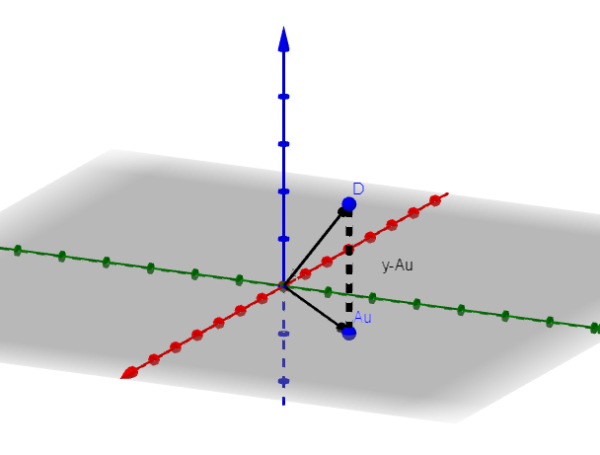
Laissez V le vecteur minimisant. Dans la figure, nous observons que Y-AU est minimisé lorsqu'il est orthogonal à l'image d'un. Autrement dit, si V est le vecteur minimisant, alors il arrive que:

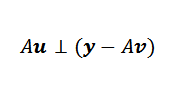
Ensuite, nous pouvons exprimer ce qui précède de cette manière:

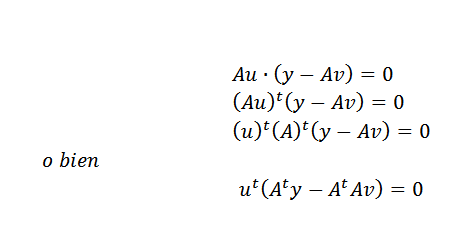
Cela ne peut arriver que si:

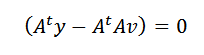
Enfin, en nettoyant V, nous devons:

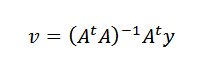
Il est possible de le faire depuis^tA est inversible chaque fois que les N points car les données ne sont pas colinéaux.

Maintenant, si au lieu de chercher une ligne, nous souhaitons trouver une parabole (dont l'expression serait de la forme y = a + bx + cx²) Qu'il s'agissait d'une meilleure approximation des points de données, la procédure serait décrite ci-dessous.

Peut vous servir: nombres entiers

Si les points de données étaient dans cette parabole, il faudrait:

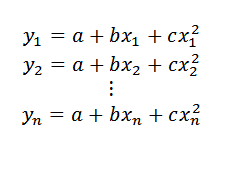
Alors:

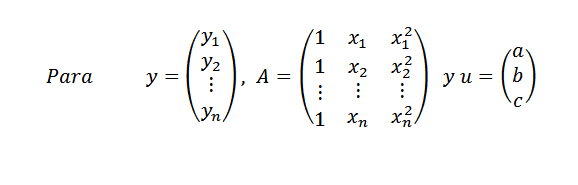
De même, nous pouvons écrire y = Au. Si tous les points ne sont pas dans la parabole, nous avons que Y-AU est différent de zéro pour tout vecteur u et notre problème est à nouveau: trouvez un vecteur u dans R3 tel que sa norme || y-Au || être autant que possible.

Répéter la procédure précédente, nous pouvons accéder au vecteur recherché est:

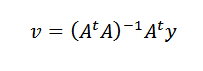
Exercices résolus

Exercice 1

Trouvez la ligne qui convient le mieux aux points (1.4), (-2,5), (3, -1) et (4.1).

Solution

Nous devons:

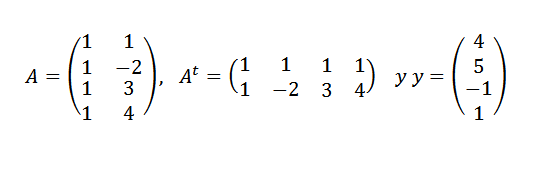
Alors:

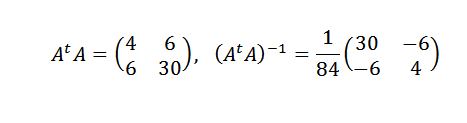
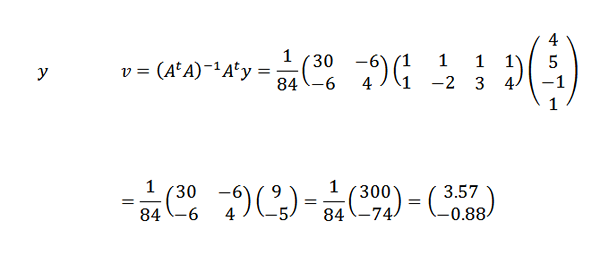
Par conséquent, nous concluons que la ligne qui convient le mieux aux points est donnée par:

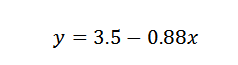
Exercice 2

Supposons qu'un objet soit tombé d'une hauteur de 200 m. En chute, les mesures suivantes sont prises:

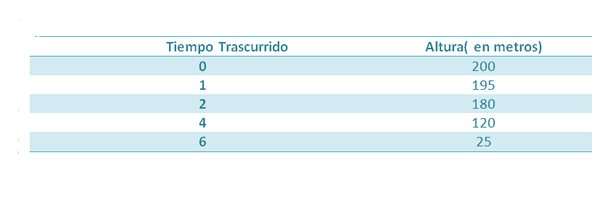
Nous savons que la hauteur de cet objet, après un temps s'est écoulé, est donnée par:

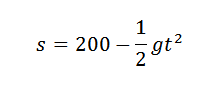
Si nous souhaitons obtenir la valeur de G, nous pouvons rechercher une parabole qui est une meilleure approche des cinq points donnés dans le tableau, et donc nous aurions que le coefficient qui accompagne T² Ce sera une approche raisonnable de (-1/2) g si les mesures sont exactes.

Nous devons:

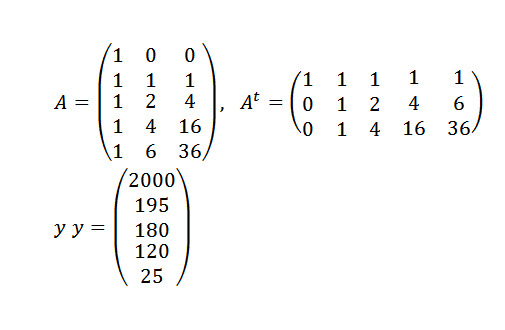
Et après:

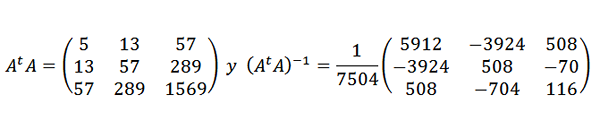
Ainsi, les points de données sont ajustés par l'expression quadratique suivante:

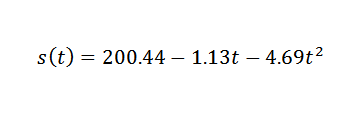
Vous devez donc:

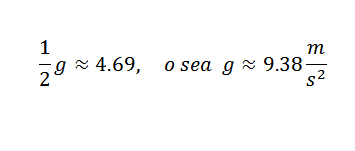
C'est une valeur raisonnablement proche du bon, qui est g = 9,81 m / s². Afin d'obtenir un g plus précis de g, il serait nécessaire de commencer des observations plus précises.

Quelle est la méthode carrée minimale pour?

Dans les problèmes qui se produisent en sciences naturelles ou sociales, il est pratique d'écrire les relations entre différentes variables à travers une expression mathématique.

Peut vous servir: variation proportionnelle

Par exemple, nous pouvons raconter en économie le coût (c), le revenu (i) et les bénéfices (U) via une formule simple:

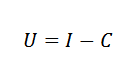
En physique, nous pouvons relier l'accélération causée par la gravité, le temps où un objet a chuté et la hauteur de l'objet par la loi:

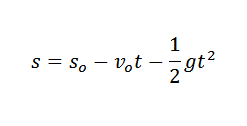
Dans l'expression précédente s_soit C'est la hauteur initiale dudit objet et V_soit est votre vitesse initiale.

Cependant, trouver des formules comme celles-ci n'est pas une tâche simple; Il correspond généralement au professionnel en service de travailler avec de nombreuses données et d'exécuter à plusieurs reprises plusieurs expériences (afin de vérifier que les résultats obtenus sont constants) pour trouver des relations entre les différentes données.

Une façon courante d'y parvenir est de représenter les données obtenues dans un plan comme points et de rechercher une fonction continue qui aborde de manière optimale ces points.

L'une des façons de trouver la fonction selon laquelle "les meilleures approches" les données fournies sont par la méthode des minimums carrés.

De plus, comme nous l'avons également vu dans l'exercice, grâce à cette méthode, nous pouvons réaliser des approches assez étroites des constantes physiques.