Mesures de position, tendance centrale et dispersion

Le Mesures du centre, de la dispersion et de la tendance de la position, Ce sont des valeurs utilisées pour interpréter correctement un ensemble de données statistiques. Ceux-ci peuvent être travaillés directement, comme obtenu à partir de l'étude statistique, ou ils peuvent être organisés en groupes de fréquence égale, facilitant l'analyse.

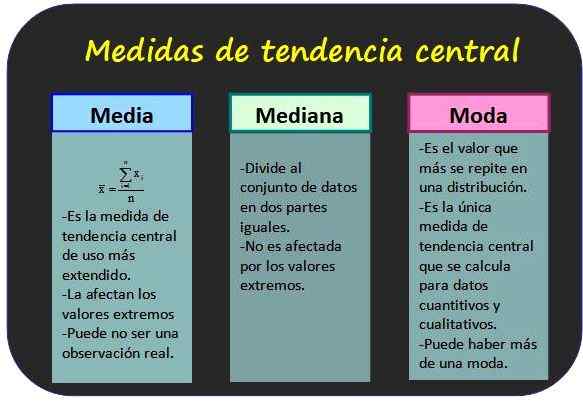
Les trois mesures de tendance centrales les plus connues et certaines de ses propriétés. Source: F. Zapata.

Mesures de tendance centrale

Ils permettent de savoir quelles valeurs les données statistiques sont regroupées.

Moyenne arithmétique

Il est également connu comme la moyenne des valeurs d'une variable et est obtenue en ajoutant toutes les valeurs et en divisant le résultat par le nombre total de données.

• Moyenne arithmétique pour les données sans regroupement

Être une variable x dont il n'y a pas de données sans organiser ou regroupement, sa moyenne arithmétique est calculée comme suit:

Et en notation sommaire:

Exemple

Les propriétaires d'une auberge de touriste de montagne ont l'intention de savoir combien de jours en moyenne les visiteurs restent dans les installations. Pour ce faire, un record des jours de permanence de 20 groupes de touristes a été réalisé, obtenant les données suivantes:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

Les jours moyens que les touristes restent est:

= 2.5 jours

• Moyenne arithmétique pour les données groupées

Si les données variables sont organisées dans un tableau de fréquence absolue F_Toi Et les centres de classe sont x₁, X₂,…, X_n, La moyenne est calculée par:

Dans la sommation de l'été:

Médian

La médiane d'un groupe de n valeurs de n variable x est la valeur centrale du groupe, à condition que les valeurs soient de plus en plus ordonnées. De cette façon, la moitié de toutes les valeurs sont inférieures à la mode et l'autre moitié sont plus importantes.

• Moyen de données non groupées

Les cas suivants peuvent être présentés:

-Nombre n valeurs de variable x  impair: La médiane est la valeur qui est juste au milieu du groupe de valeurs:

-Nombre n valeurs de variable x paire: Dans ce cas, la médiane est calculée comme la moyenne des deux valeurs centrales du groupe de données:

Exemple

Pour trouver la médiane des données de l'auberge touristique, ils sont d'abord commandés du moins au plus grand:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Il peut vous servir: quelle est la fréquence relative et comment il est calculé?

Le numéro de données est même, donc il y a deux données centrales: x_dix et x_onze Et comme les deux valent 2, sa moyenne aussi.

Médian = 2

• Moyen de données groupées

La formule suivante est utilisée:

Les symboles de la formule signifient:

-C: Largeur d'intervalle contenant la médiane

-B_M: Bordure inférieure de ce même intervalle

-F_m: nombre d'observations contenant l'intervalle à laquelle appartient la médiane.

-N: données totales.

-F_BM: nombre d'observations avant l'intervalle contenant la médiane.

Mode

La mode pour les données non groupées est la valeur la plus fréquentielle, tandis que pour les données groupées, c'est la classe la plus fréquentielle. Il est considéré comme la mode comme les données ou classe de distribution les plus représentatives.

Deux caractéristiques importantes de cette mesure sont qu'un ensemble de données peut avoir plus d'une mode, et la mode peut être déterminée à la fois pour les données quantitatives et les données qualitatives.

Exemple

Poursuivant avec les données de l'auberge de tourisme, celle qui se répète le plus est 1, par conséquent, la chose la plus habituelle est que les touristes restent 1 jour dans l'auberge.

Mesures de dispersion

Les mesures de dispersion décrivent comment sont regroupés les données autour des mesures centrales.

Gamme

Il est calculé en soustrayant les principales données et les données mineures. Si cette différence est grande, c'est un signe que les données sont dispersées, tandis que les petites valeurs indiquent que les données sont proches de la moyenne.

Exemple

La gamme des données de l'auberge touristique est:

Plage = 5−1 = 4

Variance

• Variance pour les données non groupées

Pour trouver la variance s² Il est nécessaire de connaître d'abord la moyenne arithmétique, puis la différence est calculée au carré entre chaque données et la moyenne, toutes sont ajoutées et divisées par les observations totales. Ces différences sont connues sous le nom déviations.

La variance, qui est toujours positive (ou zéro), indique à quelle distance les observations de la moyenne: si la variance est élevée, les valeurs sont plus dispersées que lorsque la variance est petite.

Exemple

La variance pour les données de l'auberge de tourisme est:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Variance pour les données groupées

Pour trouver la variance d'un groupe de données groupées, elles sont nécessaires: i) la moyenne, ii) la fréquence f_Toi  qui est le total des données dans chaque classe et iii) x_Toi  ou valeur de classe:

Il peut vous servir: types de triangles

Écart-type

La desviación estándar es la raíz cuadrada positiva de la varianza, por lo que tiene una ventaja sobre la varianza: viene en las mismas unidades que la variable bajo estudio y así se tiene una idea más directa de lo cerca o lejos que está la variable de La moyenne.

• Écart-type pour les données non groupées

Il est déterminé simplement en trouvant la racine carrée de la variance pour les données non soumises:

 Exemple

L'écart type pour les données de l'auberge touristique est:

S = √ (s²) = √1.95 = 1.40

• Écart type pour les données groupées

Il est calculé en trouvant la racine carrée de la variance pour les données groupées:

Mesures de position

Les mesures de position divisent un ensemble de données ordonné en parts égales. La médiane, en plus d'être une mesure de tendance centrale, est également une mesure de position, car elle divise l'ensemble en deux parties égales. Mais vous pouvez obtenir des pièces plus petites avec des quartiles, des déciles et des centiles.

Quartiles

Les quartiles divisent l'ensemble en quatre parties égales, chacune avec 25% des données. Ils sont désignés comme q₁, Q₂ et alors₃ Et la médiane est le quartile Q₂. De cette façon, 25% des données sont inférieures au quartile Q₁, 50% en dessous du quartile Q₂ ou médiane et 75% sous le quartile Q₃.

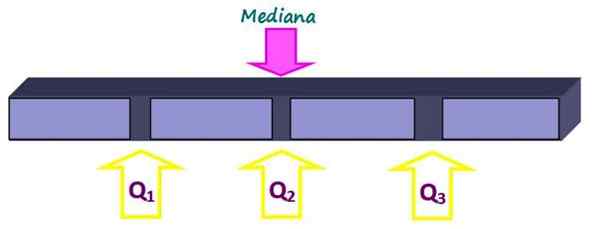Figure 2. Les quartiles divisent l'ensemble de données en quatre parties égales. Source: F. Zapata.

• Quartiles pour les données non groupées

Les données sont commandées et le total est divisé en 4 groupes avec le même nombre de données chacune. La position du premier quartile est trouvée par:

Q₁ = (n + 1) / 4

Être le total des données. Si le résultat est la totalité des données correspondant à cette position, mais si elle est décimale, les données correspondant à la partie entière avec les éléments suivants sont moyennées, ou pour une plus grande précision, elle est linéairement interpolée entre lesdites données.

Exemple

La position du premier quartile Q₁ Pour les données de l'auberge de tourisme, c'est:

Q₁ = (n + 1) / 4 = (20 + 1) / 4 = 5.25

C'est la position du quartile 1 et, comme le résultat, est décimal, les données x sont recherchées₅ et x_6, qui sont respectivement x₅ = 1 et x₆ = 1 et ils sont moyennés, résultant:

Premier quartile = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

La position du deuxième quartile Q₂ est:

Peut vous servir: somme télescopique: comment il est résolu et résolu les exercices

Q₂ = 2 (n + 1) / 4 = 10.5

Qui est la moyenne entre x_dix et x_onze et coïncide avec la médiane:

Deuxième quartile = médian = 2

La troisième position de quartile est calculée par:

Q₃ = 3 (n + 1) / 4 = 3 (20 + 1) / 4 = 15.75

Il est également décimal, donc x sont moyennés_quinze et x₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Mais comme les deux valent 4:

Troisième quartile = 4

La formule générale de la position des quartiles dans les données non soumis est:

Q_k = K (n + 1) / 4

Avec k = 1,2,3.

• Quartiles pour les données groupées

Ils sont calculés similaires à la médiane:

L'explication des symboles est:

-B_Q: bordure inférieure de l'intervalle contenant du quartile

-C: Largeur de cet intervalle

-F_q: Le nombre d'observations contenait l'intervalle de quartile.

-N: données totales.

-F_Bq: Nombre de données avant l'intervalle contenant du quartile.

Déciles et centiles

Les déciles et les centiles divisent respectivement l'ensemble de données en 10 parties égales et 100 parties égales, et leur calcul est effectué analogue à celui des quartiles.

• Déciles et centiles pour les données non groupées

Les formules sont utilisées respectivement:

D_k = K (n + 1) / 10

Avec k = 1,2,3… 9.

Décile d₅ Il doit être égal à la médiane.

P_k = K (n + 1) / 100

Avec k = 1,2,3… 99.

Le centile p_cinquante Il doit être égal à la médiane.

Exemple

Dans l'exemple de l'auberge de tourisme, la position du D₃ est:

D₃ = 3 (20 + 1) / 10 = 6.3

Comment un numéro décimal est-il moyen de x₆ et x_7, les deux égaux à 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Signifie que 3 dixièmes des données sont inférieures à x₇ = 1 et le reste ci-dessus.

• Déciles et centiles pour les données groupées

Les formules sont analogues à celles des quartiles. D est utilisé pour désigner les déciles et P pour les centiles et les symboles sont interprétés de la même manière:

La règle empirique

Lorsque les données sont distribuées symétriquement et que la distribution est unimodale, il y a une règle appelée  Règle empirique soit Règle 68 - 95 - 99, Cela les regroupe dans les intervalles suivants:

• 68% des données sont dans l'intervalle:

• 95% des données sont dans l'intervalle:

• 99% des données sont dans l'intervalle:

Exemple

Dans quel intervalle représente 95% des données de l'auberge touristique?

Ils sont dans l'intervalle: [2.5−1.40; 2.5 + 1.40] = [1.1; 3.9].

Les références

1. Berenson, M. 1985. Statistiques pour l'administration et l'économie. Inter-américain s.POUR.
2. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
3. Levin, R. 1988. Statistiques pour les administrateurs. 2e. Édition. Prentice Hall.
4. Spiegel, m. 2009. Statistiques. Série Schaum. 4 ta. Édition. McGraw Hill.
5. Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.