Magnitude vectorielle

Qu'est-ce qu'une magnitude vectorielle?

Ongle Magnitude vectorielle C'est toute expression représentée par un vecteur qui a une valeur numérique (module), une direction, une direction et un point d'application. Quelques exemples de magnitudes vectorielles sont le déplacement, la vitesse, la résistance et le champ électrique.

La représentation graphique d'une ampleur vectorielle se compose d'une flèche dont la pointe indique sa direction et sa direction, sa longueur est le module et le point de départ est l'origine ou le point d'application.

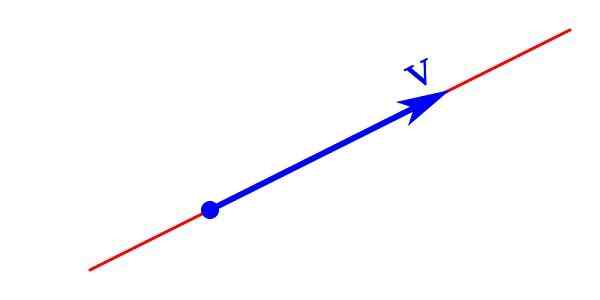
Représentation graphique d'un vecteur

L'amplitude du vecteur est représentée analytiquement avec une lettre qui transporte une flèche en haut pointant vers la droite en direction horizontale. Il peut également être représenté par une lettre écrite en gras V dont le module ǀVǀ Il est écrit en italique V.

L'une des applications du concept de magnitude vectorielle réside dans la conception des autoroutes et des routes, en particulier dans la conception de ses courbures. Une autre application est le calcul du déplacement entre deux places ou le changement de vitesse d'un véhicule.

Éléments d'une ampleur vectorielle

Une ampleur vectorielle est toute entité représentée par un segment de ligne, avec une orientation dans l'espace, qui a les caractéristiques d'un vecteur. Ses éléments sont:

Module: C'est la valeur numérique qui indique la taille ou l'intensité de l'ampleur du vecteur.

adresse: C'est l'orientation du segment de ligne dans l'espace qui le contient. Le vecteur peut avoir une direction horizontale, verticale ou inclinée; Nord, Sud, ceci ou l'ouest; Nord-est, sud-est, sud-ouest ou nord-ouest.

Sens: Il est indiqué avec la pointe de la flèche à la fin du vecteur.

Il peut vous servir: physique avant les Grecs (Grèce Antigua)

Point de demande: C'est l'origine ou le point d'action initiale du vecteur.

Classification vectorielle

Les vecteurs sont classés comme colinéaires, parallèles, perpendiculaires, simultanément, des distiques, libres, glissants, opposés, équipement, fixe et unité.

Coménéal: Ils appartiennent ou agissent sur la même ligne droite, ils sont également appelés dépendant linéairement Et ils peuvent être verticaux, horizontaux et inclinés.

Parallèles: Ils ont la même adresse ou inclination.

Perpendiculaire: Deux vecteurs sont perpendiculaires l'un à l'autre lorsque l'angle entre eux est de 90 °.

Concurrent: Ce sont des vecteurs qui, lorsqu'ils glissent sur leur ligne d'action, ils coïncident au même point dans l'espace.

Coplanarios: Ils agissent dans un avion, par exemple l'avion Xy.

Gratuit: Ils se déplacent n'importe où dans l'espace en gardant leur module, leur direction et leur signification.

Glisser: Ils se déplacent le long de la ligne d'action déterminée par leur direction.

Opposés: Ils ont le même module et la même direction, et la même direction opposée.

Équipement: Ils ont le même module, direction et signification.

Fixé: Le point de demande a invariable.

Unitaires: Vecteurs dont le module est l'unité.

Composants vectoriels

Une magnitude vectorielle dans un espace à trois dimensions est représentée dans un système de trois axes perpendiculaires les uns aux autres (X y Z) appelé orthogonal essayé.

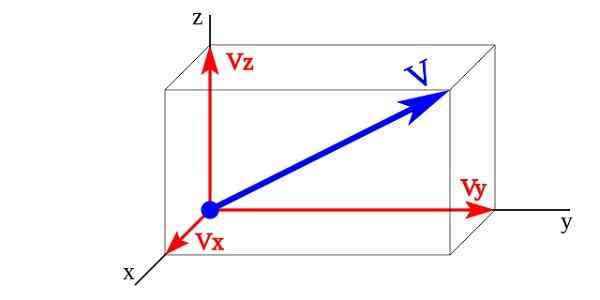Composants vectoriels d'une magnitude vectorielle

Dans l'image, les vecteurs Vx, Vy, Vz sont les composants vectoriels vectoriels V dont les vecteurs unitaires sont X,et,z. L'amplitude vectorielle V Il est représenté par la somme de ses composants vectoriels.

V = Vx + Vy + Vz

Le résultat de plusieurs amplitudes vectorielles est la somme vectorielle de tous les vecteurs et remplace ces vecteurs dans un système.

Champ vectoriel

Le champ vectoriel est la région de l'espace dans lequel à chacun de ses points une ampleur vectorielle correspond. Si l'ampleur qui se manifeste est une force agissant sur un corps ou un système physique, le champ vectoriel est un champ de forces.

Peut vous servir: Théorème de Steiner: explication, applications, exercices

Le champ vectoriel est représenté graphiquement par des lignes de champ qui sont des lignes tangents de l'amplitude vectorielle à tous les points de la région. Quelques exemples de champs vectoriels sont le champ électrique créé par une charge électrique ponctuelle dans l'espace et le champ de vitesse d'un fluide.

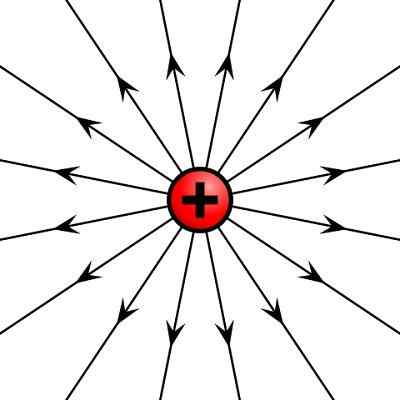Champ électrique créé par une charge électrique positive

Opérations avec des vecteurs

Ajout de vecteurs: C'est le résultat de deux vecteurs ou plus. Si vous avez deux vecteurs SOIT et P La somme est SOIT + P = q. Le vecteur Q C'est le vecteur résultant qui est obtenu en déplaçant graphiquement l'origine du vecteur POUR à la fin du vecteur B.

Soustraction vectorielle: La soustraction de deux vecteurs ou et P est SOIT - P = Q. Le vecteur Q  Vous obtenez en ajoutant au vecteur SOIT Votre contraire -P. La méthode graphique est la même que la somme avec la différence que le vecteur opposé est transféré à l'extrême.

Produit scalaire: Le produit d'une ampleur scalaire pour par une ampleur vectorielle P C'est un vecteur Député qui a la même direction du vecteur P. Si l'amplitude scalaire est zéro, le produit scalaire est un vecteur nul.

Exemples de magnitudes vectorielles

Position

La position d'un objet ou d'une particule par rapport à un système de référence est un vecteur qui est donné par ses coordonnées rectangulaires X y Z, et est représenté par ses composants vectoriels Xî, Yĵ, Zk. Les vecteurs  Toi, ĵ, k Ce sont des vecteurs unitaires.

Une particule à un moment donné (X y Z) a un vecteur de position r = Xî + Yĵ + Zk. La valeur numérique de la position vectorielle est r= √ (X² + et² + z²). Le changement de position de particules d'une position à une autre par rapport à un système de référence est le vecteur Déplacement Δr Et il est calculé avec l'expression vectorielle suivante:

Peut vous servir: rayons anodiques

Δr = r₂ - r₁

Accélération

Accélération moyenne (pour_m) Il est défini comme la variation de la vitesse V Dans un intervalle de temps Δt Et l'expression pour le calculer est pour_m= Δv / Δt, être ΔV La vitesse de changement vectorielle.

Accélération instantanée (pour) est la limite de l'accélération moyenne pour_m quand Δt devient si petit qu'il tend à zéro. L'accélération instantanée est exprimée en fonction de ses composants vectoriels

pour =pour_XToi +pour_et ĵ+ pour_zk

Champ gravitationnel

La force d'attraction gravitationnelle exercée par une masse M, Situé à l'origine, sur une autre messe m À un moment de l'espace X, et, z C'est un champ vectoriel appelé champ de force gravitationnelle. Cette force est donnée par l'expression:

F= (-mmg /r)ȓ

r = Xî + Yĵ + Zk

F = C'est la force gravitationnelle de la magnitude physique

G = est la constante de gravitation universelle

ȓ = le vecteur de position de masse est-il m

Les références

1. Tallack, J C. Introduction à l'analyse vectorielle. Cambridge: Cambridge University Press, 2009.
2. Spiegel, M R, Lipschutz, S et Spellman, D. Vecteur d'analyse. s.l. : MC Graw Hill, 2009.
3. Marque, L. Vecteur d'analyse. New York: Dover Publications, 2006.
4. Griffiths, D J. Introduction aux électodynamiques. New Jersey: Prentice Hall, 1999. p. 1-10.
5. Haye, B. Une introduction à l'analyse vectorielle. Glasgow: Methuen & Co. Ltd, 2012.