Algèbre vectorielle
- 972
- 254
- Jade Duval
Quelle est l'algèbre vectorielle?
Il Algèbre vectorielle Il s'agit d'une branche des mathématiques en charge des systèmes d'étude d'équations linéaires, de vecteurs, de matrices, d'espaces vectoriels et de leurs transformations linéaires. Il est lié à des domaines tels que l'ingénierie, la résolution des équations différentielles, l'analyse fonctionnelle, la recherche opérationnelle, les graphiques informatiques, entre autres.
Une autre des domaines que l'algèbre linéaire a adoptée est la physique, car à travers cela, il a été possible de développer l'étude des phénomènes physiques, les décrivant par l'utilisation de vecteurs. Cela a rendu possible une meilleure compréhension de l'univers.
Fondamentaux
L'algèbre vectorielle provient de l'étude des quaternions (extension des nombres réels) 1, i, j et k, ainsi que la géométrie cartésienne promue par Gibbs et Heaviside, qui a réalisé que les vecteurs serviraient d'instrument à représenter plusieurs phénomènes physiques.
L'algèbre vectorielle est étudiée par trois fondations:
Géométriquement
Les vecteurs sont représentés par des lignes qui ont une orientation, et des opérations telles que la somme, la soustraction et la multiplication par des nombres réels sont définis par des méthodes géométriques.
Analytiquement
La description des vecteurs et de leurs opérations est effectuée avec des nombres, appelés composants. Ce type de description est le résultat d'une représentation géométrique car un système de coordonnées est utilisé.
Axiomatiquement
Une description des vecteurs est faite, quel que soit le système de coordonnées ou tout type de représentation géométrique.
L'étude des figures dans l'espace se fait par sa représentation dans un système de référence, qui peut être dans une ou plusieurs dimensions. Parmi les principaux systèmes figurent:
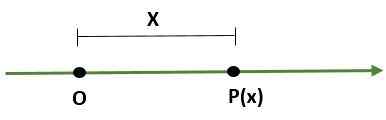
- Système unidimensionnel, qu'il s'agit d'une ligne où un point (ou) représente l'origine et un autre point (P) détermine l'échelle (longueur) et la direction de ceci:

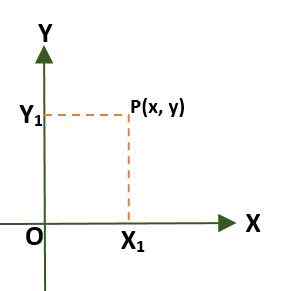
- Système de coordonnées rectangulaires (deux dimensions), qui est composée de deux lignées perpendiculaires appelées axe x et y, qui passent à travers une origine de point (ou); De cette façon, le plan est divisé en quatre régions appelées quadrants. Dans ce cas, un point (p) dans le plan est donné par les distances qui existent entre les axes et P.
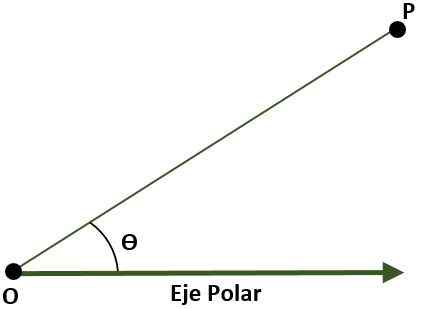
- Système de coordonnées polaires (deux dimensions). Dans ce cas, le système est composé d'un point O (origine) qui est appelé poteau et un semi--river avec origine ou appelé axe polaire. Dans ce cas, le point P du plan, en référence au poteau et à l'axe polaire, est donné par l'angle (ɵ), qui est formé par la distance entre l'origine et le point P.
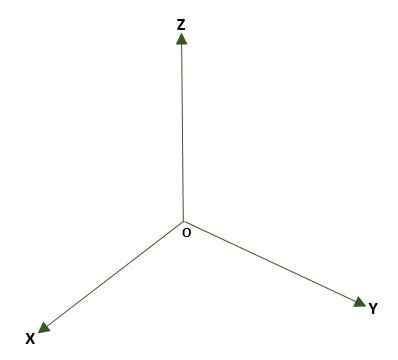
- Système rectangulaire à trois dimensions, formé par trois lignes perpendiculaires (x, y, z) qui ont comme point ou dans l'espace. Trois plans de coordonnées sont formés: XY, XZ et YZ; L'espace sera divisé en huit régions appelées octants. La référence d'un point P de l'espace est donnée par les distances qui existent entre les plans et P.
Grandeur
Une ampleur est une quantité physique qui peut être comptée ou mesurée par une valeur numérique, comme dans le cas de certains phénomènes physiques; Cependant, il est souvent nécessaire de décrire ces phénomènes avec d'autres facteurs qui ne sont pas numériques. C'est pourquoi les amplitudes sont classées en deux types:
Ampleur scalaire
Ce sont ces quantités qui sont définies et représentées de manière numérique; c'est-à-dire par un module avec une unité de mesure. Par exemple:
A) Temps: 5 secondes.
b) Masse: 10 kg.
c) Volume: 40 ml.
D) température: 40 ºC.
Magnitude vectorielle
Ce sont ces quantités qui sont définies et représentées par un module avec une unité, ainsi que par un sens et une direction. Par exemple:
Peut vous servir: symbolisation des expressionsA) vitesse: (5ȋ - 3ĵ) m / s.
b) Accélération: 13 m / s2; S 45º E.
c) Force: 280 n, 120º.
d) Poids: -40 ĵ kg -f.
Les amplitudes vectorielles sont représentées graphiquement par des vecteurs.
Que sont les vecteurs?
Les vecteurs sont des représentations graphiques d'une magnitude vectorielle; c'est-à-dire que ce sont des segments de ligne dans lesquels sa fin finale est la pointe d'une flèche.
Ceux-ci sont déterminés par son module ou sa longueur du segment, leur sens qui est indiqué par la pointe de sa flèche et sa direction selon la ligne à laquelle il appartient. L'origine d'un vecteur est également connue sous le nom de point d'application.
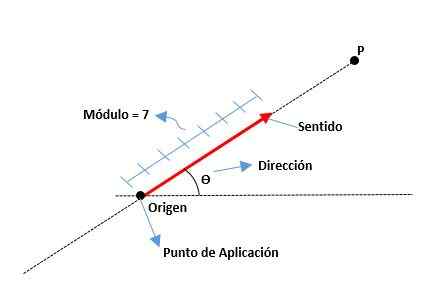
Les éléments d'un vecteur sont les suivants:
Module
C'est la distance de l'origine à la fin d'un vecteur, représenté par un nombre réel avec une unité. Par exemple:
| Om | = | A | = A = 6 cm
adresse
C'est la mesure de l'angle qui existe entre l'axe x (du positif) et le vecteur, ainsi que les points cardinaux (nord, sud, est et ouest).
Sens
Il est donné par la pointe de la flèche située à la fin du vecteur, indiquant où cela est dirigé.
Classification des vecteurs
Généralement, les vecteurs sont classés comme:
Vecteur fixe
C'est celui dont le point d'application (Origin) est fixé; c'est-à-dire qu'il reste lié à un espace d'espace, donc il ne peut pas se déplacer dans ce.
Vecteur libre
Il peut se déplacer librement dans l'espace car son origine se déplace à n'importe quel point sans changer son module, signification ou direction.
Vecteur coulissant
C'est celui qui peut transférer son origine le long de sa ligne d'action sans changer son module, signification ou direction.
Propriétés vectorielles
Parmi les principales propriétés des vecteurs sont les suivants:
Vecteurs équipocent
Ce sont ces vecteurs libres qui ont le même module, la même direction (ou ce sont parallèles) et le sens qu'un vecteur coulissant ou un vecteur fixe.
Vecteurs équivalents
Il se produit lorsque deux vecteurs ont la même adresse (ou sont parallèles), le même sens, et malgré des modules et des points d'application différents, ils provoquent des effets égaux.
Égalité vectorielle
Ceux-ci ont le même module, direction et sens, même lorsque leurs points de départ sont différents, ce qui permet à un vecteur parallèle de se déplacer vers lui-même sans l'affecter.
Vecteurs opposés
Ce sont ceux qui ont le même module et la même direction, mais leur signification est opposée.
Vecteur unitaire
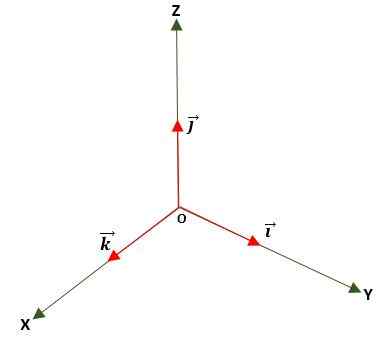
C'est celui dans lequel le module est égal à l'unité (1). Ceci est obtenu en divisant le vecteur par son module et est utilisé pour déterminer la direction et la direction d'un vecteur, soit dans le plan ou dans l'espace, en utilisant les vecteurs de base ou d'unité standardisés, qui sont:
Vecteur nul
C'est celui dont le module est égal à 0; c'est-à-dire que son point d'origine et son extrême coïncident au même point.
Composants vectoriels
Les composants d'un vecteur sont les valeurs des projections vectorielles sur les axes du système de référence; Selon la décomposition du vecteur, qui peut être dans des axes de deux ou trois dimensions, deux ou trois composants seront obtenus, respectivement.
Les composants d'un vecteur sont des nombres réels, qui peuvent être positifs, négatifs ou même zéro (0).
De cette façon, si vous avez un vecteur ā, originaire d'un système de coordonnées rectangulaires dans le plan XY (deux dimensions), la projection sur l'axe x est āx et la projection sur l'axe y et est āy. Ainsi, le vecteur sera exprimé comme la somme de ses vecteurs de composants.
Exemples
Premier exemple
Vous avez un vecteur à part de l'origine et les coordonnées de ses extrémités sont données. Ainsi, le vecteur ā = (āX; POURet) = (4; 5) cm.
Peut vous servir: 120 diviseurs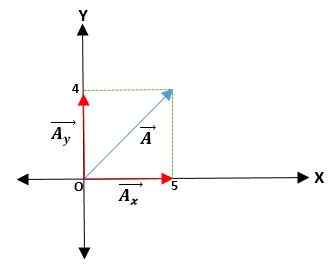
Si le vecteur ā agit à l'origine d'un système de coordonnées triangulaires à trois dimensions (dans l'espace) x, y, z, à un autre point (p), les projections de leurs axes seront āx, āy et āz; Ainsi, le vecteur sera exprimé comme la somme de ses trois vecteurs de composants.
Deuxième exemple
Vous avez un vecteur à part de l'origine et les coordonnées de ses extrémités sont données. Ainsi, le vecteur ā = (aX; POURet; POURz) = (4; 6; -3) cm.
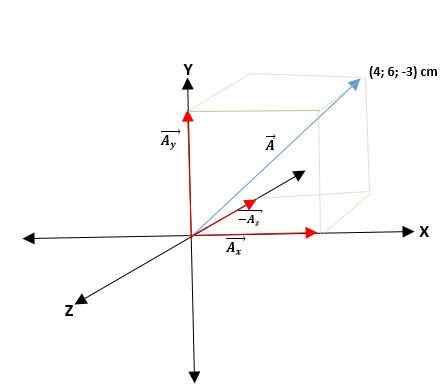
Les vecteurs qui ont leurs coordonnées rectangulaires peuvent être exprimés en fonction de leurs vecteurs de base. Pour cela, seule chaque coordonnée doit être multipliée par son vecteur d'unité respectif, de sorte que pour l'avion et l'espace, ils seront les suivants:
Pour l'avion: ā = aXi + aetJ.
Pour l'espace: ā = aXi + aetJ + Azk.
Opérations avec des vecteurs
Il existe de nombreuses amplitudes qui ont un module, une signification et une direction, comme l'accélération, la vitesse, le déplacement, la force, entre autres.
Ceux-ci sont appliqués dans divers domaines de la science, et pour les appliquer, il est nécessaire dans certains cas d'effectuer des opérations telles que la somme, la soustraction, la multiplication et la division des vecteurs et des scalaires.
addition et soustraction des vecteurs
La somme et la soustraction des vecteurs sont considérées comme une seule opération algébrique car la soustraction peut être écrite comme une somme; Par exemple, la soustraction des vecteurs ā et ē peut être exprimée comme suit:
Ā - ē = ā + (-ē)
Il existe différentes méthodes pour effectuer la somme et la soustraction des vecteurs: ils peuvent être des graphiques ou des analyses.
Méthodes graphiques
Utilisé lorsqu'un vecteur a un module, un sens et une direction. Pour cela, des lignes sont tracées qui forment une figure qui aide par la suite à déterminer. Parmi les plus connus sont les suivants:
Méthode de parallélogramme
Pour faire la somme ou la soustraction de deux vecteurs, un point commun est choisi sur l'axe de coordonnées - qui représentera le point d'origine des vecteurs -, maintenant leur module, direction et direction.
Ensuite, les lignes parallèles sont tracées vers les vecteurs pour former un parallélogramme. Le vecteur résultant est la diagonale qui laisse du point d'origine des deux vecteurs au sommet du parallélogramme:
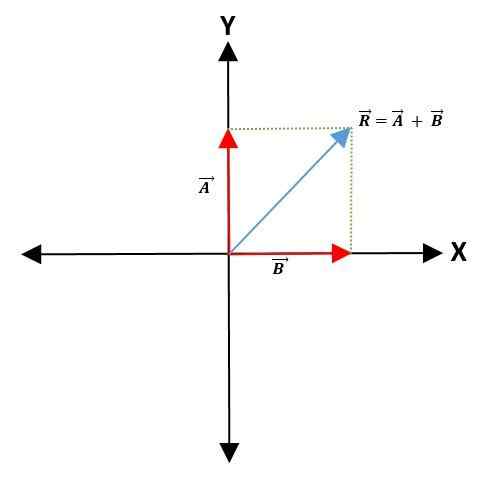
Méthode de triangle
Dans cette méthode, les vecteurs sont placés sous l'autre, en maintenant leurs modules, sens et adresses. Le vecteur résultant sera l'union de l'origine du premier vecteur avec la fin du deuxième vecteur:
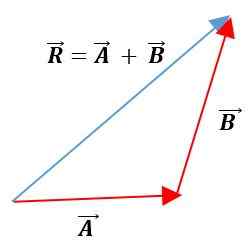
méthodes analytiques
Deux vecteurs ou plus peuvent être ajoutés ou soustraits via une méthode géométrique ou vectorielle:
Méthode géométrique
Lorsque deux vecteurs forment un triangle ou un parallélogramme, l'Odulo et la direction du vecteur résultant peuvent être déterminés en utilisant les lois du sein et du cosinus. Ainsi, le module vectoriel résultant, appliquant la loi du cosinus et par la méthode du triangle, est donné par:
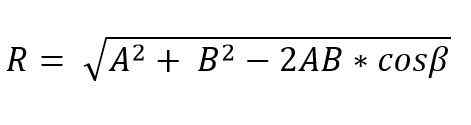
Dans cette formule, β est l'angle inverse du côté r, et cela est égal à 180º - ɵ.
D'un autre côté, par la méthode de parallélogramme, le module vectoriel résultant est:
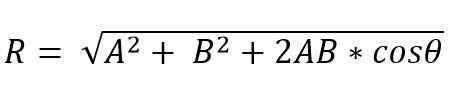
L'adresse vectorielle résultante est donnée par Angle (α), qui forme celui résultant avec l'un des vecteurs.
Selon le droit du sein, la somme ou la soustraction des vecteurs peut également être effectuée par la méthode du triangle ou du parallélogramme, sachant que dans chaque triangle, les côtés sont proportionnels aux seins des beaux angles:
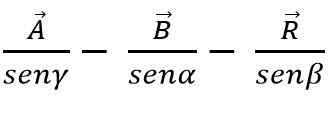
Méthode vectorielle
Cela peut être fait de deux manières: selon ses coordonnées rectangulaires ou ses vecteurs de base.
Se puede hacer trasladando los vectores que se van a sumar o restar hacia el origen de coordenadas, y luego se descomponen en sus componentes rectangulares todas las proyecciones en cada uno de los ejes para el plano (x, y) o el espacio (x, et Z); Enfin, ses composants sont ajoutés algébriquement. Donc, pour l'avion, c'est:
Peut vous servir: Nombres primo: caractéristiques, exemples, exercices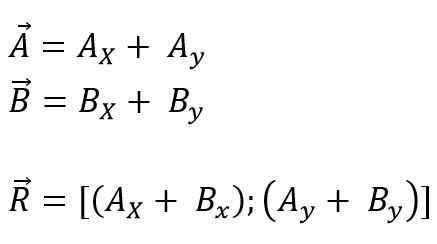
Le module vectoriel résultant est:
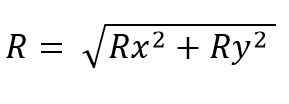
Tandis que pour l'espace, c'est:
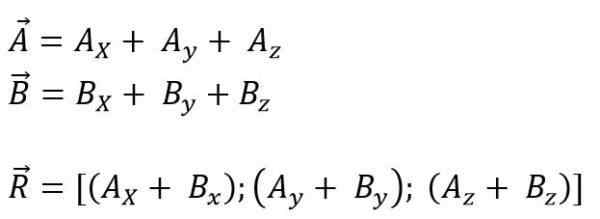
Le module vectoriel résultant est:
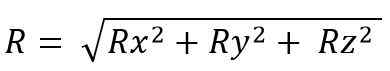
Lorsque des sommes vectorielles sont effectuées, plusieurs propriétés sont appliquées, qui sont:
- Propriété associative: Le résultat ne change pas en ajoutant d'abord deux vecteurs, puis en ajoutant un troisième vecteur.
- Propriété commutative: L'ordre des vecteurs ne modifie pas.
- Propriété distributive vectorielle: Si un scalaire est multiplié par la somme de deux vecteurs, il est égal à la multiplication du scalaire pour chaque vecteur.
- Scalaire de propriété distributive: Si un vecteur est multiplié par la somme de deux scalaires, il est égal à la multiplication du vecteur pour chaque scalaire.
Multiplication vectorielle
La multiplication ou le produit de vecteurs pourraient être effectués comme la somme ou la soustraction, mais ce faisant, elle perd le sens physique et n'est presque jamais dans les applications. Par conséquent, généralement les types de produits les plus utilisés sont le produit scalaire et vectoriel.
Produit scalaire
Il est également connu comme un point de deux vecteurs. Lorsque les modules à deux vecteurs sont multipliés par l'angle mineur cosinus qui se forme entre eux, un scalaire est obtenu. Pour exprimer un produit scalaire entre deux vecteurs, un point entre eux est placé, et cela peut être défini comme:
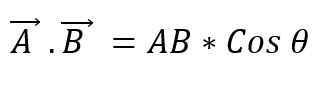
La valeur de l'angle qui existe entre les deux vecteurs dépendra de la question de savoir si celles-ci sont parallèles ou perpendiculaires; Ainsi, vous devez:
- Si les vecteurs sont parallèles et ont le même sens, coseno 0º = 1.
- Si les vecteurs sont parallèles et ont des sens opposés, Coseno 180º = -1.
- Si les vecteurs sont perpendiculaires, Coseno 90º = 0.
Cet angle peut également être calculé en sachant que:

Le produit scalaire a les propriétés suivantes:
- Propriété commutative: l'ordre des vecteurs ne modifie pas le scalaire.
- Propriété distributive: si un scalaire est multiplié par la somme de deux vecteurs, il est égal à la multiplication de scalaire pour chaque vecteur.
Produit vectoriel
La multiplication vectorielle, ou produit transversal de deux vecteurs A et B, entraînera un nouveau vecteur C et exprime à l'aide d'une croix parmi les vecteurs:
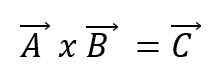
Le nouveau vecteur aura ses propres caractéristiques. De cette manière:
- La adresse: Ce nouveau vecteur sera perpendiculaire à l'avion, qui est déterminé par les vecteurs d'origine.
- Il sens: Ceci est déterminé avec la règle de droite, où le vecteur a est tourné vers le b pointant la direction de la rotation avec les doigts, et avec le pouce, la direction du vecteur est marquée.
- Il module: Il est déterminé par la multiplication des modules des vecteurs AXB, par le sein de l'angle mineur qui existe entre ces vecteurs. Il est exprimé:
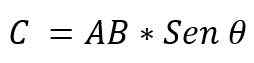
La valeur de l'angle qui existe entre les deux vecteurs dépendra de la question de savoir si celles-ci sont parallèles ou perpendiculaires. Il est donc possible d'affirmer ce qui suit:
- Si les vecteurs sont parallèles et ont la même signification, sinus 0º = 0.
- Si les vecteurs sont parallèles et ont des sens opposés, Sine 180º = 0.
- Si les vecteurs sont perpendiculaires, sinus ° = 1.
Lorsqu'un produit vectoriel est exprimé en fonction de ses vecteurs de base, il doit:
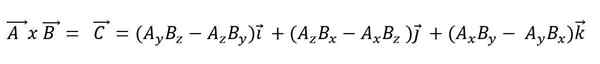
Le produit scalaire a les propriétés suivantes:
- Ce n'est pas commutatif: l'ordre des vecteurs modifie le scalaire.
- Propriété distributive: si un scalaire est multiplié par la somme de deux vecteurs, il est égal à la multiplication de scalaire pour chaque vecteur.

