Formules de loi Hooke, exemples, applications, exercices

La la loi de Hooke souligne que la déformation vécue par un objet élastique est directement proportionnelle à la force appliquée sur elle. La constante de proportionnalité dépend de la nature de l'objet, de sa géométrie et du matériau avec lequel il est fabriqué.

Tous les matériaux ont des propriétés élastiques dans une plus ou moins loin, ils se conforment donc à la loi de Hooke chaque fois qu'ils reviennent à leurs dimensions d'origine, une fois que la force cesse. Les ressorts et les gencives élastiques sont de bons exemples d'objets conformes à la loi de Hooke, mais les cabillas en acier aussi qui font partie d'un pont.

Figure 1. Loi de Hooke au printemps

Prenant comme exemple un ressort ou un quai, pour le garder étiré ou comprimé, il est nécessaire d'appliquer une force dont l'ampleur est F. Selon la loi de Hooke, le printemps connaîtra une déformation X:

F ∝ x

La constante de proportionnalité, qui, étant un printemps, est appelée raideur de printemps, Il est donc désigné comme K:

F = k⋅x

Dans les unités du système international, la Force arrive à Newton (N) et la déformation en mètres (m). Par conséquent, la constante de ressort a des unités N / M. La constante de ressort représente la force qui doit être appliquée pour la déformer en 1 m de longueur.

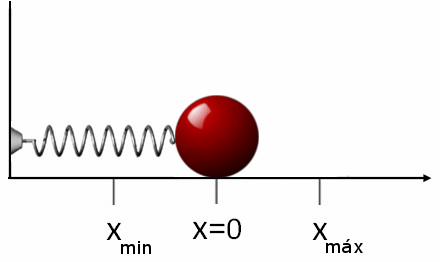Figure 2. Lorsque le ressort est étiré, la force exercée sur l'objet est contraire. La même chose se produit si le ressort rétrécit, dans ce cas, il entraîne l'objet dans le sens opposé. Source: Wikimedia Commons.

Si après avoir étiré ou comprimé le ressort, il est libéré, il se déplacera dans la direction opposée à la force appliquée. Cela signifie que si nous l'étinuons, il est compressé et vice versa. C'est pourquoi forcer f_R Quoi Les exercices du printemps est:

F_R = -K⋅X

Le signe négatif indique ce qui est dit: que la force s'oppose au déplacement, donc cette force est connue sous le nom Force réparatrice.

[TOC]

Formule et équations

La relation entre la force et le déplacement dans un printemps a été découverte par Robert Hooke (1635-1703), un physicien anglais notable et connu pour sa rivalité avec Isaac Newton. Hooke était un scientifique polyvalent qui a réussi à se souterrainer dans différents domaines de la science: mécanique, biologie, astronomie et architecture.

figure 3. Le physicien anglais Robert Hooke, qui ne connaît pas les portraits de l'époque. Ceci est une reconstruction faite par l'artiste Rita Gerer en 2004 à travers des descriptions laissées par ceux qui ont rencontré le scientifique. Source: Wikimedia Commons. Rita Greer / Fal.

Hooke s'est rendu compte que si la force appliquée à une jetée n'est pas très grande, le quai est proportionnellement se déforme pour forcer, et une fois cette force disparaît, le printemps a à nouveau sa longueur naturelle.

Peut vous servir: magnétosphère terrestre: caractéristiques, structure, gaz

De cette façon, la loi de Hooke a graphiquement la forme d'une ligne droite, dont la pente est la constante de ressort. L'image suivante montre la force exercée sur le ressort pour l'étirer - ou la comprimer - en fonction de la position x. Notez que la force ne dépend pas de la longueur naturelle du ressort, mais de son déplacement.

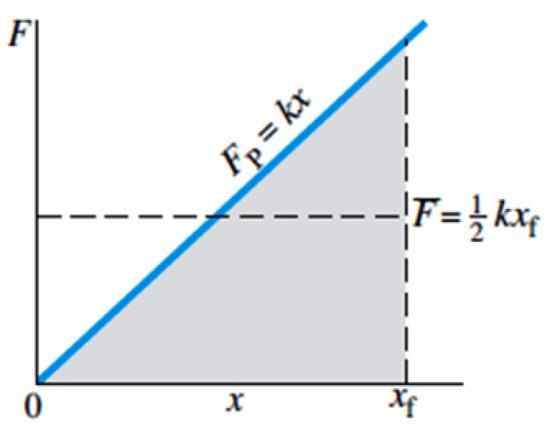Figure 4. Magnitude f de la force nécessaire pour étirer ou comprimer un ressort, en fonction de la déformation x. Source: Giancoli, D. Physique avec applications.

La force moyenne est indiquée dans le graphique par f avec barre et équivaut à ½ kx_F, Où x_F est la position finale du printemps.

La force exercée au printemps, et la force qu'il exerce sur un objet qui lui est lié, sont des forces variables. Plus vous souhaitez étirer ou compresser au printemps, plus vous devez appliquer de force pour pouvoir y parvenir.

Travail effectué pour étirer ou comprimer un printemps

Lorsqu'une force est appliquée qui déforme le ressort, un travail stocké au printemps est effectué et qui peut être utilisé plus tard.

Le travail mécanique est défini comme la zone sous le graphique de la force F en fonction de la position x. Pour calculer le travail w qu'une force variable F (x) fait lors du déplacement d'un objet de la position x₁ pour positionner x₂ L'intégrale définie doit être calculée:

Dans le cas des travaux nécessaires pour apporter un ressort de sa position d'équilibre à la position x_F Il est très simple, car la zone à calculer est celle du triangle ombré gris de la figure 4, dont la formule est connue:

Zone de triangle = ½ base. hauteur

Par conséquent, le travail nécessaire est:

W = ½ x_F . (KX_F) = ½ k (x_F)²

Et si vous souhaitez calculer le travail nécessaire pour amener au ressort de la position x à la position x_F, Il serait équivalent au calcul de la zone du trapèze rayé de la figure 5:

W = ½ k (x_F)² - ½ K x²

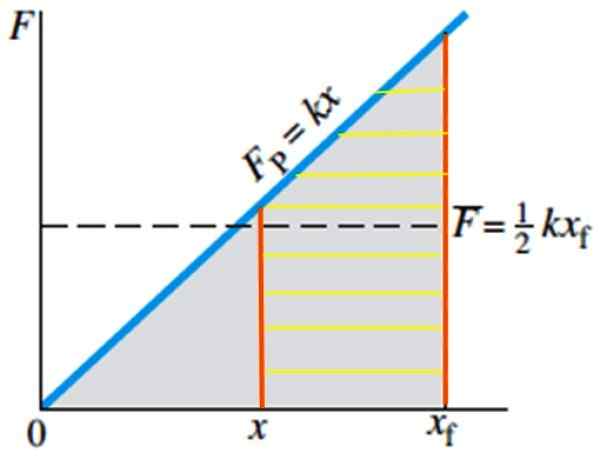Figure 5. Le travail effectué pour étirer le ressort de la position X à la position XF équivalente à la région de Rayada. Source: Giancoli, D. Physique avec applications.

Exemples de ressorts

Selon l'application à laquelle ils sont destinés, les ressorts peuvent être cylindriques, coniques, en spirale, avec une section transversale circulaire (la plus courante), de section carrée ou rectangulaire.

Peut vous servir: conducteurs électriques

Une classification largement utilisée est en fonction du type d'effort auquel ils seront soumis: il y a des ressorts de torsion, de flexion, de compression et d'extension. Ces derniers sont largement utilisés et il travaille également pour la tension et la compression.

Ressort de compression

Un exemple de ressort de compression est ce qui est utilisé dans le jouet appelé Pogo soit Saltoín Palo. Ces ressorts stockent une énergie assez potentielle lorsqu'elles sont compressées et libérées progressivement tout en retournant à la position d'équilibre. De cette façon, les rebonds ne sont pas trop brusques.

Figure 6. Pogo ou Saltoín Stick est basé sur un ressort de compression. Source: Wikimedia Commons.

Springs d'extension et de torsion

Le ressort pour les cordes est le type de ressorts d'extension et sont fabriqués avec des tours bien interrogés, avec deux crochets aux extrémités. Ils sont capables de conserver suffisamment d'énergie potentielle, qu'ils libèrent plus tard lorsque quelqu'un se lève et commence à sauter sur la toile, qui a également sa propre réponse élastique, comme tous les matériaux.

Les ressorts de torsion sont très courants, car ils servent à faire des pinces à vêtements. Au lieu de crochets aux extrémités, ils se penchent à angle, pour résister aux forces qui ont tendance à exercer une torsion.

Figure 7. Les ressorts font partie d'innombrables mécanismes, tels que ces vêtements de vêtements. Source: pxfuel.

Matériaux pour la fabrication de ressorts

Les matériaux les plus appropriés pour fabriquer des ressorts sont ceux avec un Résistance ultime (résistance finale), c'est-à-dire qu'ils soutiennent un grand effort avant de se briser. Il est également pratique que le matériau ait un point de fluage élevé, afin qu'il ne perde pas ses qualités élastiques avec de petits efforts.

Les ressorts à usage industriel sont fabriqués avec des alliages qui incluent l'acier à haute teneur en carbone, en cuivre, en nickel et en bronze.

Applications de droit de Hooke

Comme les ressorts ont la vertu du stockage d'énergie potentielle lorsqu'ils s'étirent ou se compressent, ils sont capables de travailler en déplaçant des choses comme des mécanismes.

De cette façon, les ressorts ont de nombreuses applications, des petits objets quotidiens, à travers les voitures, aux machines de toutes sortes. Les ressorts servent à:

-Vibrations de choc.

-Fabriquer des mécanismes rétractables: stylo, pincettes suspendues, crochets de cheveux.

-Faire le printemps ou les dynamomètres

Et ils font également partie du mécanisme de:

Peut vous servir: circuit électrique fermé

-Montres.

-Trampolines.

-Écluses.

-Jouets.

-Armes.

-Les compteurs d'aiguille, par exemple le galvanomètre, utilisés pour mesurer les courants, tensions et résistances.

Exercices résolus

- Exercice 1

Une force de magnitude 5 est appliquée.0 n à un ressort, faisant une longueur de 3 tronçon.5 cm de sa longueur naturelle.

a) Combien est étiré lorsque la force appliquée est de 7 N?

b) Trouvez le travail effectué par la force appliquée pour s'étirer au printemps 3.5 cm de sa longueur naturelle.

Solution à

Sachant que le printemps est étiré 3.5 cm par l'application de 5.0 n nous pouvons calculer votre constante:

k = f / x = 5.0 n / 3.5 cm = 1.43 n / cm.

Lorsqu'une force de 7 n est appliquée, le tronçon suivant est obtenu:

x = f / k = 7.0 n / 1.43 n / m = 4.9 cm

Solution B

Le travail nécessaire pour déformer un printemps est donné par:

W = ½ kx² = 0.5 x 1.43 n / cm x (3.5 cm)² = 8.76 N . cm = 8.76 N . 1 x10 ^-2 m = 0.0876 J.

- Exercice 2

Une source de pâte méprisable et de 10 cm de long est suspendue à un soutien. Si une masse de 2 kg est pendue, le ressort est étiré jusqu'à atteindre 15 cm. Calculer:

a) la constante de ressort

b) La taille du ressort lorsqu'une masse de 3 kg est suspendue.

Solution à

Le tronçon de ressort est x = 15 - 10 cm = 5 cm

Comme le système est en équilibre statique, la force exercée par le ressort lors de l'étirement est dirigée verticalement vers le haut, pour compenser le poids, qui est dirigée vers le bas, puis:

F_R = W → kx = mg

K = 2 x 9.8 n / 5 x10 ^-2 M = 392 n / m

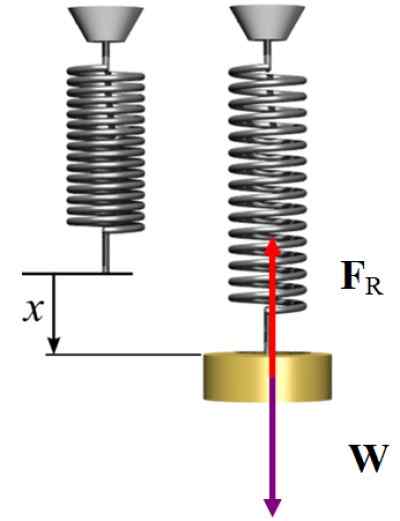Diagramme corporel libre pour l'exercice résolu 2. Source: Wikimedia Commons / F. Zapata.

Solution B

Lorsqu'un poids de 3 kg est suspendu, la nouvelle force est w = 3 x 9.8 n = 29.4 N

Dans ce cas, le tronçon est:

x = mg / k = 29. 4 n / 392 n / m = 0.075 M = 7.5 cm

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Blog des mécanismes créatifs. Quatre types de ressorts différents. Récupéré de: CreativeMechanisms.com.
3. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. 2ieme volume. Dynamique. Édité par Douglas Figueroa (USB).
4. Giancoli, D.  2006. Physique: principes avec applications. 6e. Élégant. Prentice Hall.
5. Chevalier, r.  2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique.  Pearson.