La loi de Fick

Quelle est la loi de Fick?

La La loi de Fick C'est une équation mathématique qui relie le flux massique diffusé dans un milieu avec les concentrations ou les pressions gradient. Il a été formulé en 1855 par le physiologiste allemand et docteur Adolf, qui inspiré par les lois de Fourier (conduction thermique) et l'OHM (conduction électrique), a modélisé le processus de diffusion de l'oxygène aux alvéoles des poumons.

La loi de Fick présente la particularité qu'elle ne s'applique pas seulement aux phénomènes de diffusion chimique ou biochimique, mais à ceux de tout type de nature. Par conséquent, il sert à modéliser la diffusion des atomes entre les solides, étant très utile dans la physique des matériaux et de l'ingénierie.

Représentation d'un processus de diffusion à travers une membrane semi-perméable. Source: Gabriel Bolívar.

Cependant, la base centrale est la même pour presque tous les phénomènes de diffusion, qui est illustré ci-dessus. Les particules violettes, les atomes ou les molécules, sont réparties à travers une membrane épais semi-perméable L et une zone transversale pour. À gauche, nous avons une concentration plus élevée C₁ de particules qui à droite, c₂.

La loi de Fick établit ce qui suit: le flux massique diffusé à travers une surface est proportionnel au gradient de concentration (c₂-C₁/ L) et une constante d appelée coefficient de diffusion ou de diffusivité.

Cette loi a deux formes: une basée sur l'espace (x), et une autre en fonction de l'espace et du temps (x, t). Le premier s'applique aux systèmes dans des conditions stationnaires, tandis que la seconde pour les systèmes réels non stationnaires.

La première loi de Fick

Composants et équation

La l épaisse de la membrane semi-perméable représente la distance (x) que les particules doivent voyager pour atteindre l'autre côté. Comme on peut le voir dans l'image, les particules violettes plus elles s'éloignent du compartiment gauche, où c₁ C'est génial, sa concentration diminue à la valeur de C₂. C'est-à-dire que la concentration change le long de l'épaisseur de la membrane, dépendant de x.

Cette variation de concentration en fonction de la distance est ce qu'on appelle le gradient de concentration: (c₂-C₁) / L o (c₂-C₁)/X. Notez que sa valeur est négative (-1), car c₂ > C₁.

D'un autre côté, nous avons également la vitesse à laquelle les particules sont réparties à travers la membrane ou l'espace en question. Cette vitesse dépend de la taille et de la masse des particules, ainsi que de la nature de l'environnement et de la température. Le coefficient de diffusion d représente cette vitesse et peut être constant ou non pendant la diffusion.

Peut vous servir: filtre de laboratoire): caractéristiques, fonctions, types

Et enfin, nous avons un flux massique «J» qui traverse la zone transversale de la membrane ou du canal où les particules se propagent. En regroupant ces termes, l'équation de la première loi de Fick est née:

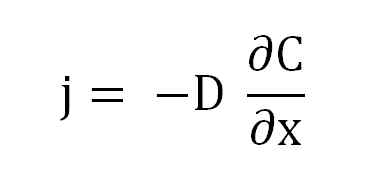Équation de la première loi de Fick. Source: Gabriel Bolívar.

Où j est proportionnel à d et a (∂c / ∂x), le gradient de concentration.

Interprétation et unités

Le symbole négatif dans l'équation sert à neutraliser le signe négatif du gradient de concentrations. Sinon, j aurait une valeur négative, qui n'est pas intégrée. De même, la valeur de d est positive, de sorte qu'en multipliant par le signe négatif qui le précède, il donne une valeur négative.

La première loi de Fick indique ce qui suit: Plus le gradient de concentration est élevé (∂c / ∂x), plus le flux de masse est élevé J. C'est-à-dire la différence entre c₂ et C₁ Il devient plus grand et, par conséquent, plus de particules se propageront à travers la membrane.

D'un autre côté, J dépend également de D, qui à son tour dépend de paramètres tels que la température, la viscosité, le poids moléculaire et la zone transversale à:

D ∝ (A / L) (S / √m_W)

Où S est la solubilité de la particule qui se propage avec l'environnement, et m_W Son poids moléculaire.

Concernant les unités des composants ou les termes de l'équation que nous avons:

-C (kg · m^-3 ou mol · m^-3)

-D (M^-2· S^-1)

-J (kg · m^-2· S^-1 ou mol · m^-2· S^-1)

Déplacement quadratique moyen net

Pendant la diffusion, les particules entrent en collision les unes avec les autres, et après de courts intervalles de temps finissent par parcourir les distances énormes Δx. Cependant, selon la signification de ces déplacements, Δx peut avoir des valeurs négatives ou positives (selon un point d'origine). C'est pourquoi la moyenne des valeurs Δx pour toutes les molécules tend à 0.

D'un autre côté, les valeurs Δx sont très petites par rapport aux distances qui exécutent les particules. Lorsqu'ils entrent en collision, ils perdent la mobilité vers une direction, ayant par conséquent un déplacement net limité; Par exemple, 2 cm avancent dans une direction après avoir parcouru des centaines de mètres en collisions et rebonds.

Einstein en 1905 a trouvé une expression mathématique pour le parchemin moyen du déplacement (donc différent de 0):

<(Δx)²> = 2dt

Déterminant

(Δx)_RMS ≡ <(Δx)²>^1/2 = (2dt)^1/2

(Δx)_RMS Il s'agit du déplacement quadratique net moyen des particules en question. (Δx)_RMS Il nous dit combien de particules se déplacent en moyenne (dans une direction positive ou négative) en fonction du temps. Certaines particules se déplaceront plus ou les plus proches que (Δx)_RMS, provoquant une distribution gaussienne.

Peut vous servir: oxyde de calcium (CAO)

Deuxième loi

Équation

La première loi de Fick décrit la diffusion dans des conditions stationnaires, c'est-à-dire que le flux massique J ne varie pas dans le temps. Dans les systèmes réels, cependant, nous avons des conditions non stationnaires, où le flux massique varie non seulement dans l'espace, mais aussi au fil du temps. Par conséquent, il est intéressé à déterminer (∂c / ∂t).

Ci-dessous, nous avons deux équations qui représentent la deuxième loi de Fick:

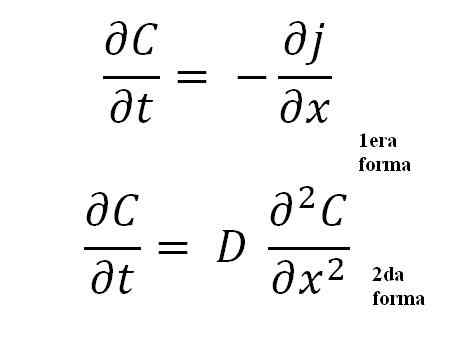Équations de la deuxième loi de Fick. Source: Gabriel Bolívar.

La deuxième forme est la plus importante de toutes, car elle représente l'équation mathématique générale pour tout processus de diffusion; soit thermique, électrique, atomique, etc.

Déduction

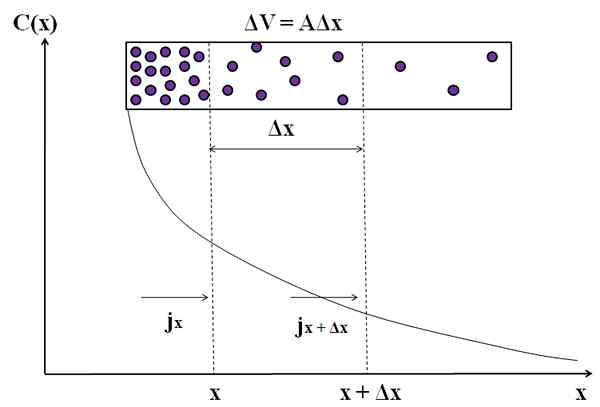Représentation graphique de la façon dont le flux de masse n'est pas constant dans la diffusion de ces molécules. Source: Gabriel Bolívar.

Considérez à nouveau les particules violettes dans une chambre rectangulaire. Parmi les distances x et x + Δx, nous avons un flux j_X (entrant) et J_{x + Δx} (sortant). Le volume de la caméra entre ces distances est défini par:

Δv = aΔx

Notez que le graphique c (x) vs x ne provient pas d'une ligne droite, nous avons donc des valeurs différentes de J (J_X ≠ j_{x + Δx}). Nous devons déterminer ΔC / Δt.

La masse m_X Il sera égal à:

m_X = J_X Ajus

Une analyse dimensionnelle aide à comprendre pourquoi:

kg = (kg · m^-2· S^-1) (m²) (S)

De la même manière que nous calculons m_{x + Δx}:

m_{x + Δx} = J_{x + Δx} Ajus

Étant la masse qui s'accumule dans cette région égale à Δm:

Δm = m_X - m_{x + Δx}

= (J_X - J_{x + Δx}) AΔt

= - (J_{x + Δx} - J_X) AΔt

= -ΔjaΔt

Et sachant que Δc = Δm / ΔV

Δc = -ΔjaΔt / Δv

= -ΔjaΔt / aΔx

= -ΔjΔt / Δx

Nous effacons Δc / Δt

Δc / Δt = -Δj / Δx

Cette expression indique que la variation de la concentration dans le temps est égale à la variation du flux J par rapport à son déplacement. En appliquant les limites pour ΔT et Δx tendant à 0, nous obtenons la même expression qu'un dérivé partiel:

∂c / ∂t = - (∂j / ∂x) (1ère forme)

Enfin, le 2ème formulaire est obtenu en remplaçant J par la première loi de Fick:

∂c / ∂t = -∂ / ∂x (-d∂c / ∂x)

= D (∂²C / ∂x²) (2e formulaire)

Exercices résolus

Dans les exercices suivants, des systèmes très simples seront pris en compte dont les inconnues peuvent être résolues à l'aide de la première loi de Fick.

Exercice 1

Déclaration

Dans un tuyau de 15 mètres de long et 21 centimètres de large, et qui est également saturé d'azote, un courant d'oxygène se propage d'une extrémité à une autre à une température de 0 ºC. Sachant que la pression sur le côté gauche (P₁) est 20 kg / m³, Et que la pression sur le côté droit (P₂) est 10 kg, déterminer:

Il peut vous servir: Ion hydronio

a) Le débit massique qui est réparti

b) Combien de kilogrammes ou₂ Ils se propageront à travers le tuyau en 17 minutes?

c) le gradient de concentration ou les pressions

d) la pression de o₂ à une distance de 7 mètres de l'entrée du pipeline

e) combien 80 kg de O₂ en se propageant à travers ce tuyau?

Considérez que d_O2-N2 est égal à 1.8 · 10^-5 m²· S^-1.

Résolution

D'après la première loi de Fick, nous devons résoudre le paragraphe a):

J = -d (p₂-P₁) / L

= - (1.8 · 10^-5 m²· S^-1) (10-20) (kg / m³) / (15 m)

= 1.2 · 10^-5 kg · m^-2· S^-1

À b) nous avons besoin de la zone de tuyau:

A = π (0.21 m)²

= 0.14 m²

Et nous multiplions j par a et temps t pour déterminer la masse de ou₂ Déshanté:

m_O2 = (1.2 · 10^-5 kg · m^-2· S^-1) (17 s) (0.14 m²)

= 3.57 · 10^-5 kg

Maintenant, pour le paragraphe c), nous avons que le gradient est égal à:

Gradient = (p₂-P₁) / L

= (10-20) (kg / m³) / 15 m

= -2/3 (kg / m³) · M^-1

Mais nous prenons la valeur positive, ce qui a un sens physique:

2/3 (kg / m³) · M^-1

Cette valeur nous servira alors à résoudre la sous-section d) si le gradient est bien interprété: chaque mètre la pression ou₂ 2/3 kg / m tombera³. En répartissant 7 mètres, nous aurons:

2/3 (kg / m³) · M^-1 (7 m) = 14/3 ou 4.7 kg / m³

C'est-à-dire que la pression à cette distance sera:

(20-4.7) (kg / m³) = 15.3 kg / m³

Et enfin, le paragraphe e) est similaire à b), seulement que nous effacions maintenant le temps et non la masse:

m_O2 = Jat

t = m_O2/ Ja

= (80 kg) / (1.2 · 10^-5 kg · m^-2· S^-1) (0.14 m²)

= 47619.04 S ou 0.55 jours

Exercice 2

Déclaration

Déterminer (Δx)_RMS Pour le saccharose dans l'eau à t = 1 min, 1 h et 1 jour. Le coefficient de dissémination du saccharose dans l'eau est 0.52 · 10^-5cm²· S^-1.

Résolution

Nous appliquons l'équation:

(Δx)_RMS ≡ <(Δx)²>^1/2 = (2dt)^1/2

Nous évaluons (Δx)_RMS Avec les temps exprimés en quelques secondes. Pour t = 1 min ou 60 s:

(Δx)_RMS = ((2 (0.52 · 10^-5cm²· S^-1) (60S))^1/2

= 0.025 cm

Pour t = 1 h ou 3600 s:

(Δx)_RMS = ((2 (0.52 · 10^-5cm²· S^-1) (3600s))^1/2

= 0.19 cm

Et enfin pour t = 1 jour ou 86400 s:

(Δx)_RMS = ((2 (0.52 · 10^-5cm²· S^-1) (86400S))^1/2

= 0.95 cm

Notez que, au fil du temps, les molécules de saccharose n'ont même pas pu déplacer 1 cm dans aucune direction.

Les références

1. Walter J. Moore. (1963). Chimie physique. Dans la cinétique chimique. Quatrième édition, Longmans.
2. L'Iran. Levine. (2009). Principes de la physicochimie. Sixième édition. Mc Graw Hill.
3. Introduction à la science et à l'ingénierie des matériaux. (11 mars 2018). La deuxième loi de Fick. Prof. Rajesh Prasad. [VIDÉO]. Récupéré de: youtube.com
4. Wikipédia. (2020). Lois de diffusion de Fick. Récupéré de: dans.Wikipédia.org
5. Laura Dickson. (10 septembre 2020). LA DIFFUSION. CHIMISTER BOOLISTexts. Récupéré de: Chem.Bibliothèque.org
6. Larissa Zhou et al. (1er septembre 2015). Comprendre la théorie de la diffusion et la loi de Fick à travers la nourriture et la cuisine. L'American Physiological Society. est ce que je.org / 10.1152 / Advan.00133.2014