Explication de la loi de Coulomb, formule et unités, exercices, expériences

La Droit de Coulomb C'est la loi physique qui régit l'interaction entre les objets chargés électriquement. Il a été déclaré par le scientifique français Charles Augustin de Coulomb (1736-1806), grâce aux résultats de ses expériences à travers l'équilibre de la torsion.

En 1785, Coulomb a connu d'innombrables temps avec de petites sphères chargées électriquement, par exemple en apportant ou en éloignant deux sphères, variant l'ampleur de sa charge et aussi son signe. Toujours regarder et enregistrer soigneusement chaque réponse.

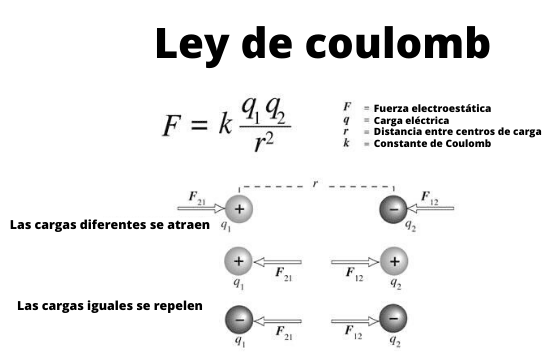
Figure 1. Schéma qui montre l'interaction entre des charges électriques spécifiques grâce à la loi de Coulomb.

Ces petites sphères peuvent être considérées comme charges spécifiques, c'est-à-dire des objets dont les dimensions sont insignifiantes. Et ils accomplissent, comme on le sait depuis l'époque des Grecs anciens, que les charges du même signe sont repoussées et celles d'un signe différent sont attirés.

Figure 2. L'ingénieur militaire Charles Coulomb (1736-1806) est considéré comme le physicien le plus important en France. Source: Wikipedia Commons.

Dans cet esprit, Charles Coulomb a trouvé ce qui suit:

-La force d'attraction ou de répulsion entre deux charges spécifiques est directement proportionnelle au produit de l'ampleur des charges.

-Cette force est toujours dirigée le long de la ligne qui rejoint les charges.

-Enfin, l'ampleur de la force est inversement proportionnelle au carré de la distance qui sépare les charges.

[TOC]

Formule et unités de la loi Coulomb

Grâce à ces observations, Coulomb a conclu que l'ampleur de la force F Entre deux frais spécifiques q₁ et q₂, séparé une distance r, Il est mathématiquement donné comme:

Comme la force est une ampleur vectorielle, pour l'exprimer, un vecteur unitaire est complètement défini r Dans le sens de la ligne qui rejoint les charges (un vecteur unitaire a une amplitude égale à 1).

De plus, la constante de proportionnalité nécessaire transformant l'expression précédente en une égalité est appelée k_et ou simplement k: le constante électrostatique soit Coulomb constante.

Enfin, la loi de Coulomb pour les charges ponctuelles est établie, donnée par:

La force, comme toujours dans le système international des unités, est disponible à Newton (N). Quant aux accusations, l'unité est appelée Coulomb (c) en l'honneur de Charles Coulomb et enfin la distance R se situe en mètres (m).

Observant attentivement l'équation précédente, il est clair que la constante électrostatique doit avoir des unités de n.m² / C², Pour obtenir des Newtons en conséquence. La valeur de la constante a été déterminée expérimentalement comme:

Peut vous servir: vecteurs gratuits: propriétés, exemples, exercices

k_et = 8.89 x 10 ⁹ N.m² / C² ≈ 9 x 10 ⁹ N.m² / C²

La figure 1 illustre l'interaction entre deux charges électriques: lorsqu'ils sont le même signe, ils sont repoussés, sinon ils attirent.

Notez que la loi de Coulomb correspond à la troisième loi ou à la loi de l'action et de la réaction de Newton, donc les amplitudes de F₁ et F₂ Ils sont les mêmes, l'adresse est la même, mais les sens sont opposés.

Comment appliquer la loi de Coulomb

Pour résoudre les interactions entre les charges électriques, ce qui suit doit être pris en compte:

- L'équation est appliquée exclusivement dans le cas de charges spécifiques, c'est-à-dire des objets chargés électriquement mais de très petites dimensions. Si les objets chargés ont des dimensions mesurables, il est nécessaire de les diviser en très petites charges, puis d'ajouter les contributions de chacune de ces charges, pour lesquelles un calcul complet est requis.

- La force électrique est une ampleur vectorielle. S'il y a plus de deux charges qui interagissent, la force nette sur la charge q_Toi Il est donné par le principe de superposition:

F_Filet = F_i1 + F_I2 + F_i3 + F_i4 +… = ∑ F_ij

Où l'indice J Vale 1, 2, 3, 4 ... et représente chacune des charges restantes.

- Il doit toujours être cohérent avec les unités. Le plus fréquent est de travailler avec la constante électrostatique en unités si, alors vous devez vous assurer que les charges sont dans Coulomb et les distances en mètres.

- Enfin, l'équation est appliquée lorsque les charges sont en équilibre statique.

Exercices résolus

- Exercice 1

Dans la figure suivante, il y a deux charges spécifiques + q et + 2q. Une troisième charge ponctuelle - Q est placée sur p. Il est invité à trouver la force électrique sur cette charge en raison de la présence des autres.

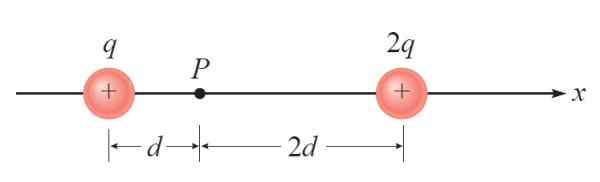figure 3. Diagramme pour l'année résolu 1. Source: Giambattista, un. La physique.

Solution

La première chose est d'établir un système de référence approprié, qui dans ce cas est l'axe horizontal ou l'axe x. L'origine de ce système peut être n'importe où, mais par confort, elle sera placée dans P, comme le montre la figure 4A:

Peut vous servir: Bethelgeuse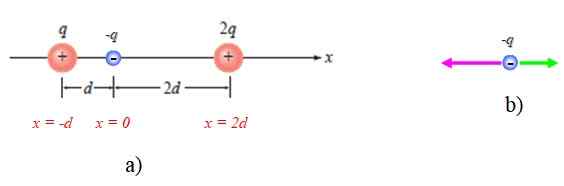Figure 4. Le régime pour l'année résolu 1. Source: Giambattista, un. La physique.

Un schéma des forces sur -Q est également montré, en tenant compte du fait qu'il est attiré par les deux autres (figure 4B).

Appelons F₁ À la force qui exerce la charge qui sur la charge -Q, ils sont dirigés le long de l'axe x et des points au sens négatif: par conséquent:

Le vecteur unitaire dans la direction de l'axe x est X Avec un accent circonflexe dans l'équation. Ceci est une notation commune pour un vecteur unitaire. Le moins signe apparaît parce que la force F₁ points au sens négatif de l'axe.

Analogue est calculée F₂:

Notez que l'ampleur de F₂ C'est la moitié du F₁, Bien que la charge soit double. Pour trouver la force nette, ils sont enfin ajoutés vectoriels F₁ et F₂:

F_Filet = (-k + k / 2).(Q² /d²) (X) N = - (k / 2).(Q² /d²) (X) N

- Exercice 2

Deux sphérites en polystyrène de masse égale m = 9.0 x 10^-8 kg ont la même charge positive Q et sont suspendus par un fil de soie en longueur L = 0,98 m. Les sphères sont séparées une distance de D = 2 cm. Calculer la valeur de.

Solution

La situation de la déclaration est décrite dans la figure 5A.

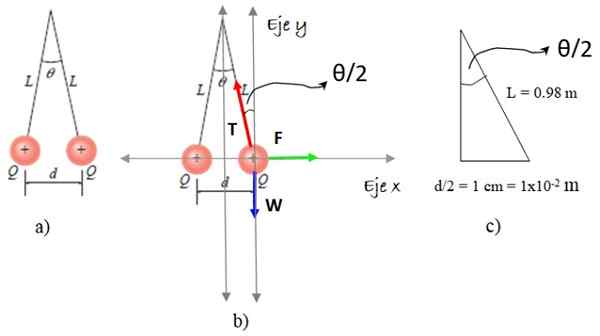Figure 5. Schémas de résolution de l'exercice 2. Source: Giambattista, un. Physique / f. Zapata.

Nous avons choisi l'une des sphérites et sur elle, nous dessinons le diagramme corporel isolé, qui comprend trois forces: le poids W, Tension de corde T et répulsion électrostatique F, comme apparaît dans la figure 5b. Et maintenant les étapes:

Étape 1

La valeur de θ / 2 est calculée avec le triangle de la figure 5c:

θ / 2 = Arcsen (1 x 10^-2/ 0.98) = 0.585º

Étape 2

Ensuite, vous devez appliquer la deuxième loi et le match de Newton 0, car les charges sont en équilibre statique. Il est important de souligner cette tension T Il est incliné et a deux composantes:

∑F_X = -T.sin θ + f = 0

∑F_et = T.cos θ - w = 0

Étape 3

Nous nettoyons l'ampleur de la tension de la dernière équation:

Il peut vous servir: Dynamique: Histoire, quelles études, lois et théories

T = w / cos θ = mg / cos θ

Étape 4

Cette valeur est remplacée dans la première équation pour trouver l'ampleur de F:

F = t sin θ = mg (sin θ / cos θ) = mg. Tg θ

Étape 5

Comme f = k q² /d², Il efface Q:

En remplaçant les valeurs numériques fournies par l'instruction, il est obtenu:

Q = 2 × 10^-onze C.

Expériences

Vérifier la loi de Coulomb est simple au moyen d'un équilibre de torsion similaire à celui utilisé dans son laboratoire.

Il y a deux petites sphères de Saúco, dont une, celle au centre de l'équilibre, est suspendue à un fil. L'expérience consiste à toucher les sphères Saúco téléchargées avec une autre sphère métallique chargée de chargement q.

Figure 6. Balance de torsion de Coulomb.

Immédiatement, la charge est répartie également entre les deux sphères Saúco, mais alors, comme les charges du même signe, ils repoussent. Une force qui provoque la torsion du fil du fil et s'éloigne immédiatement de la sphère fixe agit sur la sphère suspendue.

Ensuite, nous voyons qu'il va plusieurs fois jusqu'à ce que l'équilibre atteigne. Ensuite, la torsion de la barre ou du fil qui la tient est équilibrée par la force de répulsion électrostatique.

Si les sphères étaient à l'origine à 0, maintenant la sphère mobile aura tourné un angle θ. En entourant l'équilibre, il y a une bande supérieure en degrés pour mesurer cet angle. Lorsqu'il a précédemment déterminé la constante de torsion, alors la force de répulsion et la valeur de la charge acquise par les sphères Saúco sont facilement calculées.

Les références

1. Figueroa, D. 2005. Série: Physique pour la science et l'ingénierie. Volume 5. Électrostatique. Édité par Douglas Figueroa (USB).
2. Giambattista, un. 2010. La physique. Deuxième édition. McGraw Hill.
3. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
4. Resnick, r. 1999. Physique. Vol. 2. 3e édition. en espagnol. Société de rédaction continentale S.POUR. de c.V.
5. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. 2ieme volume.