Formule de droit de Biot-Savart, démonstration, applications, exercices

La Loi bioteuse établit une relation entre le champ magnétique dB  en un point P, produit par un fil mince qui transporte un courant I et dont la longueur différentielle est ds. Cette loi est utilisée pour trouver le champ magnétique des distributions de courant à travers le Principe de superposition. 

Cela signifie que pour calculer le champ magnétique total au point P, nous devons ajouter toutes les contributions que chaque partie différentielle Ds du fil contribue. Et cette somme est effectuée par une intégrale effectuée sur toute la distribution actuelle.

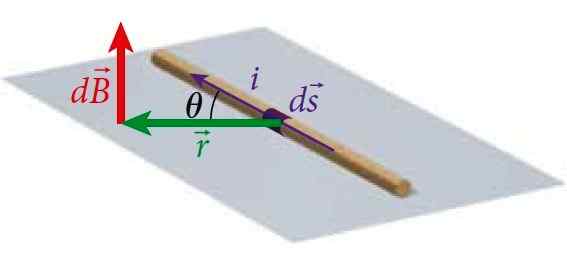
Figure 1. Un segment de fil transporte un courant I, qui produit un champ magnétique à un point P à une certaine distance du fil, qui est calculé par la loi de Biot-Savart. Source: Bauer, W. Physique pour l'ingénierie et les sciences.

De cette façon, vous pouvez calculer le champ qui produit des fils avec le courant de différentes géométries.

La loi de Biot-Savart est nommée d'après les deux physiciens français qui l'ont découverte en 1820: Jean Marie Biot (1774-1862) et Felix Savart (1791-1841). Pour y parvenir, ils ont dû étudier l'intensité et la forme du champ magnétique produit par de nombreuses distributions actuelles.

[TOC]

Formule

L'expression mathématique de la loi sur les biot-économies est la suivante:

Il maintient des analogies avec son équivalent pour calculer le champ électrique: la loi de Coulomb, seulement que le champ magnétique DB en p est perpendiculaire à l'avion où se trouve le fil. Nous pouvons le voir dans la figure 1.

L'expression précédente peut également être écrite comme suit:

Dans les deux expressions, r C'est le vecteur de position, dirigé à partir de l'élément de courant d'IDs au point où vous souhaitez calculer le champ.

Peut vous servir: conservation de l'élan linéaire: principe, exemples, exercices.

Pour sa part, r Avec un accent circumflejo, c'est le vecteur unitaire qui est dirigé dans sa même direction et sens, mais avec un module égal à 1. Le vecteur r Il est représenté comme suit:

Pour cette raison, en remplaçant dans l'équation précédente - celle qui a r³ Dans le dénominateur - l'expression r est immédiatement atteinte² Dans le dénominateur.

En plus des vecteurs susmentionnés, la formule contient la constante μ_soit, appel Perméabilité sous vide et dont la valeur est:

μ_soit = 4π x10^-7 T.M / A.

Si nous voulons calculer le vecteur de champ magnétique, il est nécessaire d'intégrer toute la distribution actuelle, pour laquelle nous avons besoin des données sur sa géométrie:

Le produit vectoriel et la règle de droite

La loi Biot-Savart implique un produit vectoriel entre les vecteurs IDs et r. Le résultat d'un produit vectoriel entre deux vecteurs est également un vecteur.

Dans ce cas, le module de produit Vector ID Vectors X r est: (ids) ⋅r⋅ssenθ, où θ est l'angle entre ids et r, comme le montre la figure 1.

De cette façon, l'ampleur du champ DB Il est donné par:

La direction et le sens peuvent être déterminés avec la règle de la main droite, qui est illustrée sur cette figure:

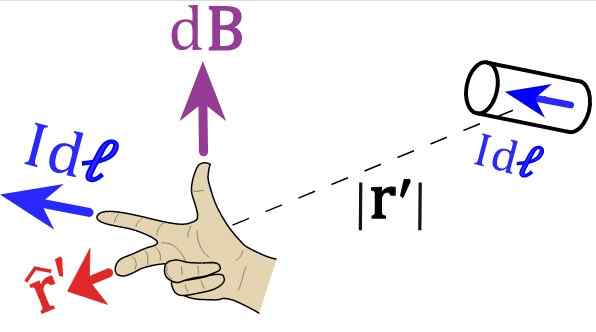Figure 2. Règle de la main droite pour la loi sur les biot-économies. Source: Wikimedia Commons.

Nous invitons le lecteur à positionner sa main droite en suivant les vecteurs des figures 1 et 2. Pour la figure 1, l'index doit pointer vers la gauche, ID suivants ou identifiantl, Le majeur pointe selon le vecteur r unitaire.

Et enfin le pouce est dirigé vers le haut et c'est la direction du champ magnétique.

Peut vous servir: ellipsoïde: caractéristiques et exemples

Démonstration de la loi biot-arône

La loi de Biot-Savart est éminemment expérimentale, ce qui signifie que sa formulation provient de nombreuses observations sur le comportement du champ magnétique produit par les fils actuels.

Observations de Biot et Savart

Ce sont les observations des scientifiques français sur le champ magnétique DB:

-L'ampleur de DB est inversement proportionnel à r².

-Il est également directement proportionnel à l'ampleur de l'élément de courant, qui est appelé IDs Et aussi à sen θ, où θ est l'angle entre les vecteurs ds et r.

-dB est perpendiculaire aux deux ids -la direction du courant - pour r.

-Diversifié de dB est tangentiel à un cercle radio r en fil. En d'autres termes, le champ B produit par un segment actuel se compose de circonférences concentriques aux stériles.

-Le sens dans lequel il tourne B Il est donné par la règle du pouce droit: le pouce droit est pointé vers la direction du courant et les quatre doigts restants sont enroulés autour du fil, après la circulation du champ.

Toutes ces observations sont combinées dans l'expression mathématique de la loi décrite précédemment.

Demandes de droit de Biot-Savart

Lorsque la distribution actuelle a une symétrie élevée, l'intégrale peut être facilement résolue, voyons certains cas:

Rectilinéaire et fil mince

Un fil rectiligne de longueur l transporte un courant i, comme celui qui apparaît sur la figure.

Il illustre la géométrie nécessaire pour le calcul du champ. Ceci est perpendiculaire à la feuille de papier, sortant à l'avion si le courant circule de gauche à droite, et entrant autrement (vérifiez-le avec la règle de la main droite).

Peut vous servir: paramagnétisme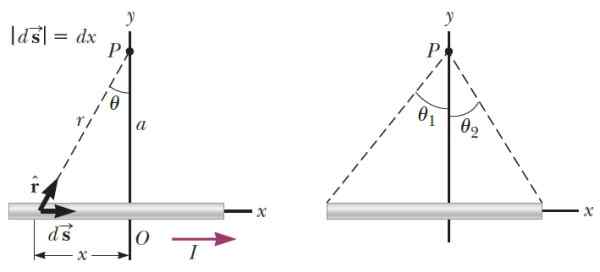figure 3.- À gauche, la géométrie nécessaire pour calculer le champ magnétique qui produit un segment de fil mince au point P. À droite les angles qui déterminent la position de p par rapport aux extrémités du segment. Source: Serow, R. Physique pour la science et l'ingénierie.

Être k  Le vecteur unitaire dans la direction perpendiculaire au plan, après avoir effectué le processus d'intégration, le champ magnétique que le fil produit en P est:

Spira circulaire

La boucle radio-circulaire pour Il transporte un courant comme indiqué sur la figure et produit un champ magnétique DB -en vert foncé - au point P sur l'axe axial, à distance X du centre.

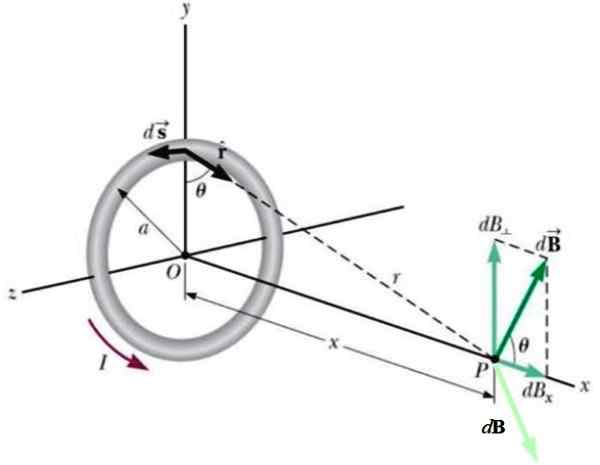Figure 4.- Géométrie pour le calcul du champ produit par la spase circulaire au point P sur l'axe axial. Source: Wikimedia Commons.

Un autre élément actuel situé du côté opposé produirait une autre contribution au DB (vert clair), de sorte que son composant vertical est annulé avec le premier.

Le résultat est que le champ magnétique net est horizontal, il n'est donc intégré que dans ces composants, ce qui entraîne:

Exercice résolu

Il y a un fil extrêmement long qui transporte un courant de 2 pour couler comme indiqué dans l'image. Calculez l'amplitude du champ magnétique à une distance radiale de 5 cm du fil.

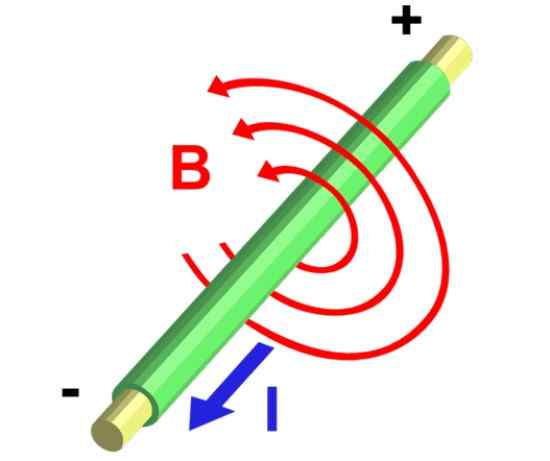Figure 5.- Lignes de champ magnétique d'un segment de fil rectiligne qui transporte le courant. Source: Wikimedia Commons.

Solution

Puisqu'il s'agit d'un très long fil, nous pouvons prendre l'expression du segment rectiligne et faire θ₁= 0º et θ₂ = 180º pour les angles limites. Cela suffit pour la longueur du fil pour stocker l'infini.

De cette façon, nous aurons le champ est:

Qui simplifie:

Maintenant, nous remplaçons les valeurs de l'instruction:

I = 2 a

R = 5 x10^-2 m

μ_soit= 4π x10^-7 T.M / A

La direction et le sens de B Ils sont illustrés à la figure 5, où la direction qui laisse la feuille a été prise comme k.

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Figueroa, D. 2005. Série: Physique pour la science et l'ingénierie. Volume 6. Électromagnétisme. Édité par Douglas Figueroa (USB).
3. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
4. Resnick, r. 1999. Physique. Vol. 1. 3e édition. en espagnol. Société de rédaction continentale S.POUR. de c.V.
5. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.
6. SERAY, R., Jewett, J. 2008. Physique pour la science et l'ingénierie. 2ieme volume. 7e. Élégant. Cengage Learning.