Interpolation de Lagrange

Quelle est l'interpolation de Lagrange?

L'interpolation de Lagrange est une méthode numérique d'approximation des fonctions, qui utilise un polynôme qui passe par certains points connus de la fonction qui vise à approximer.

Si la fonction approximative est douce, même en dehors des valeurs données ou connues, le polynôme prend les valeurs proches de celles de la fonction d'intérêt, surtout si ces valeurs se trouvent entre les points donnés. C'est pourquoi le polynôme est considéré comme une bonne approche de la fonction.

Figure 1.- Formule pour construire des polynômes de Lagrange. Source: F. Zapata.

Maintenant, supposons que vous souhaitiez approximer une fonction f (x) dont seules leurs valeurs sont connues dans certains X-_Toi-, avec Toi depuis 0 jusqu'à N-1. C'est-à-dire qu'ils se connaissent n points (X-_Toi, et_Toi) avec et_Toi = f (x_Toi), Où l'index Toi Va de 0 jusqu'à N-1.

Dans la méthode d'interpolation de Lagrange, le polynôme qui aborde la fonction f (x) C'est un polynôme P (x) degré de degré N-1, construit par la combinaison linéaire de n Polynômes L_Toi(X) degré de degré N-1. Ceux-ci sont le Polynômes de Lagrange, qui sont exprimés comme suit:

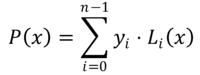
Les valeurs de et_Toi Ils représentent les ordonnées correspondant à l'abscisse X_Toi Où la fonction f (x) On sait, c'est-à-dire: et_Toi = f (x_Toi).

Polynômes de Lagrange

Grâce à des combinaisons linéaires entre eux, les polynômes de Lagrange agissent comme une base pour construire un polynôme de qualité N -1 qui servira à interpoler le n points connus.

La notation pour les polynômes est L_Toi(x), avec l'index I dans la plage de 0 à N-1. La formule pour établir les polynômes de Lagrange est la suivante:

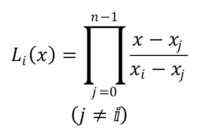
Le symbole indiqué indique que le produit des monomiaux N -1 doit être effectué, à partir du polynôme j = 0.

Caractéristiques des polynômes de Lagrange

1.- Les polynômes de Lagrange sont exactement les mêmes que l'unité lorsqu'ils sont évalués dans l'abscisse correspondant à leur index, c'est-à-dire:

L_Toi(X_Toi) = 1

2.- Ils sont annulés dans l'abscisse des points d'interpolation avec un index différent de celui du même polynôme:

Peut vous servir: statistiques descriptives: historique, caractéristiques, exemples, concepts

L_Toi(X_J) = 0, avec i ≠ j.

3.- Prenant d'autres valeurs d'abscissa différentes des points d'interpolation, les polynômes de Lagrange acquièrent des valeurs entre -1 et +1.

4.- Pour obtenir des polynômes de Lagrange, il est seulement nécessaire de connaître l'abscisse des points à Interpoch.

Polynômes de lagrange de deuxième dedeaux

Les polynômes de lagrange du deuxième degré sont ceux qui sont utilisés le plus souvent lorsque vous voulez faire une interpolation à trois points.

Supposons que la fonction interpolaire soit connue en trois points, qui sont:

(X₀,et₀); (X₁, et₁); (X₂, et₂)

Puis vos polynômes de Lagrange correspondants L₀, L₁ et L₂ Ils obtiennent comme ça:

L₀(x) = [(x - x₁) / (X₀ - X₁)] [(x - x₂) / (X₀ - X₂)]

L₁(x) = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)]

L₂(x) = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)]

Il convient de noter que L₀(X₀) = L₁(X₁) = L₂(X₂) = 1, tandis que L_Toi(X_J) = 0 toujours que Toi≠ j.

Polynôme d'interpolation du deuxième degré

Il est important de noter que dans le polynôme d'interpolation de Lagrange, les ordonnées des points d'interpolation sont des facteurs polynomiaux de Lagrange.

De cette façon, une fois les polynômes obtenus pour certaines valeurs de l'abscisse, ils servent à calculer le polynôme d'interpolation de diverses fonctions, à condition que l'absence de l'abscisse précédemment fixe soit connue.

Dans le cas d'une interpolation de deuxième année:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

Et p (x) approche la fonction f (x) dans l'intervalle (X₀, X₂).

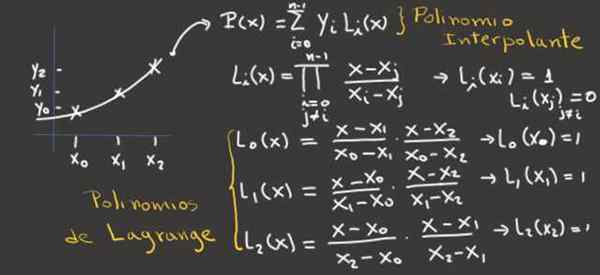Figure 2.- Cette image montre comment obtenir les polynômes de Lagrange pour trois points d'interpolation et d'eux, le polynôme interpolant. Source: F. Zapata.

Exemples

Exemple 1

Trouvez les polynômes de Lagrange correspondant à trois points d'abscissa X₀= 0, X₁= 1 et X₂= 2.

Comme le montre la section précédente, ces polynômes seront:

Peut vous servir: fonction sur-objectif: définition, propriétés, exemples

L₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( X² - 3x + 2)

L₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

L₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - X)

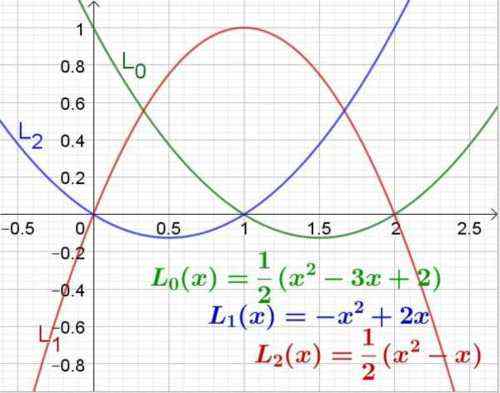figure 3. Polynômes de Lagrange pour les valeurs d'abscissa 0, 1 et 2. Source: F. Zapata.

Exemple 2

Vous souhaitez approximer la fonction f (x) = arcan (x) Dans l'intervalle [0, 2]. De cette fonction, seules leurs valeurs sont connues pour X₀= 0, X₁= 1 et X₂= 2, qui sont respectivement et₀= 0, et₁= π / 4 = 0,785 et et₂= 1 107.

Vous devez donc trouver le polynôme interpolant P (x) approchant f (x) Dans l'intervalle indiqué.

Dans l'exemple 1, les polynômes de Lagrange ont déjà été déterminés pour les valeurs d'abscissa indiquées dans cette déclaration, il n'est donc pas nécessaire de répéter le calcul. Le polynôme interpolet sera désormais:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

Ce qui équivaut à:

P (x) = y₀ L₀(x) + et₁ L₁(x) + et₂ L₂(X)

Dans ce cas spécifique, c'est:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0,785 ∙ (- x² + 2x) + 1 107 ∙ (½) (x² - X)

Ce qui précède est simplifié à:

P (x) = 0,785 ∙ (- x² + 2x) + 1 107 ∙ (½) (x² - X)

Et enfin reste:

P (x) = -0,2315 ∙ x² + 1 0165 ∙ x

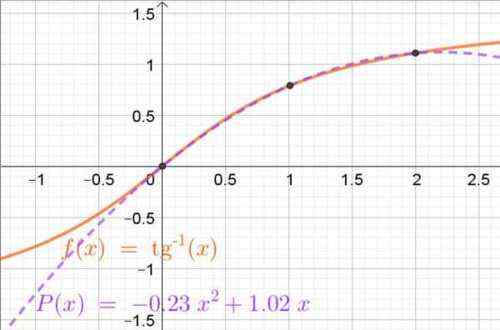Figure 4. Polynôme interpolant obtenu par des polynômes de lagrange qui se rapproche de la fonction d'arc-tangent dans l'intervalle (0, 2). Les points d'interpolation sont également affichés. Source: F. Zapata.

Exercices

Exercice 1

Obtenez des polynômes de Lagrange adéquats pour avoir une approche de la fonction:

f (x) = sin (x)

Dans l'intervalle [0, π] et avec cinq points d'interpolation.

Solution

En premier lieu, l'abscisse des points d'interpolation est déterminée, qui sont choisies égales et incluant les extrémités de l'intervalle d'approximation. Avec cela, vous avez:

X₀= 0; X₁= π / 4; X₂= π / 2; X₃= 3 π / 4; X₄= π.

Peut vous servir: inégalité du triangle: démonstration, exemples, exercices résolus

Comme f (x) est annulé aux points extrêmes, il ne sera pas nécessaire d'obtenir les polynômes Lagrange L₀ et moi₄.

Polynômes l₁, L₂ et moi₃ ils sont:

L₁ = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)] [(x - x₃) / (X₁ - X₃)] [(x - x₄) / (X₁ - X₄)]

L₂ = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)] [(x - x₃) / (X₂ - X₃)] [(x - x₄) / (X₂ - X₄)]

L₃ = [(x - x₀) / (X₃ - X₀)] [(x - x₁) / (X₃ - X₁)] [(x - x₂) / (X₃ - X₂)] [(x - x₄) / (X₃ - X₄)]

Maintenant, nous remplaçons la valeur de l'abscisse:

L₁ = [(x - 0) / (π / 4 - 0)] [(x - π / 2) / (π / 4 - π / 2)] [(x - 3 π / 4) / (π / 4 - 3 π / 4)] [(x - π) / (π / 4 - π)]

L₂ = [(x - 0) / (π / 2 - 0)] [(x - π / 4) / (π / 2 - π / 4)] [(x - 3 π / 4) / (π / 2 - 3 π / 4)] [(x - π) / (π / 2 - π)]

L₃ = [(x - 0) / (3 π / 4 - 0)] [(x - π / 4) / (3 π / 4 - π / 4)] [(x - π / 2) / (3 π / 4 - π / 2)] [(x - π) / (3 π / 4 - π)]

Les dénominateurs sont résolus:

L₁ = [x / π / 4] [(x - π / 2) / (- π / 4)] [(x - 3 π / 4) / (- π / 2)] [(x - π) / (- 3π / 4)]

L₂ = [x / π / 2] [(x - π / 4) / (π / 4)] [(x - 3 π / 4) / (- π / 4)] [(x - π) / (- π / 2)]

L₃ = [x / (3 π / 4)] [(x - π / 4) / (π / 2)] [(x - π / 2) / (π / 4)] [(x - π) / (- π / 4)]

Il est simplifié et regroupé pour obtenir:

L₁ = x (x - π / 2) (x - 3 π / 4) (x - π) / (- 3 π ⁴/ 128)

L₂ = x (x - π / 4) (x - 3 π / 4) (x - π) / (π ⁴/ 64)

L₃ = x (x - π / 4) (x - π / 2) (x - π) / (- 3 π ⁴/ 128)

Exercice 2

Obtenir le polynôme d'interpolation qui aborde la fonction Sen (x) dans l'intervalle [0, π] avec les cinq points d'interpolation choisis dans l'exercice 1 et leurs polynômes de lagrange respectifs.

Solution

Le polynôme d'interpolation est:

P (x) = sin (0) * l₀ + Sen (π / 4) * L₁ + Sen (π / 2) * L₂ + Sen (3π / 4) * L₃ + Sen (π) * L4

L'évaluation du sinus et de la fonction de multiplication est:

P (x) = (√2 / 2) L₁ + 1 * L₂ + (--√2 / 2) L₃

Après un travail algébrique ardu, le polynôme d'interpolation est:

P (x) = 2. 7481 x⁴ -quinze. 138 x³ +23. 467 x² - 9. 5236 x

Les références

1. Goodman, un. L. H. mille neuf cent quatre vingt seize. Algèbre et trigonométrie avec géométrie analytique. Pearson Education.
2. Harpe, p. d. (2000). Sujets de la théorie des groupes géométriques. University of Chicago Press.
3. Hazewinkel, m. (2001). Interpolation linéaire ", Encyclopedia of Mathematics.
4. Hoffmann, e. (2002). À la chronologie de l'interpolation: de l'astronomie ancienne au traitement moderne du signal et de l'image. Actes de l'IEEE.
5. Wikipédia. Interpolation polynomiale de Lagrange. Récupéré de: Wikipedia.com