Gradient potentiel

Quel est le gradient potentiel?

Il Gradient potentiel C'est un vecteur qui représente le rapport de changement du potentiel électrique par rapport à la distance dans chaque axe d'un système de coordonnées cartésiennes. Ainsi, le vecteur de gradient potentiel indique que l'adresse dans laquelle le taux de change du potentiel électrique est plus élevée, selon la distance.

À son tour, le module de gradient potentiel reflète le taux de variation de la variation du potentiel électrique dans une direction particulière. S'il y a une connaissance de la valeur de cela à chaque point d'une région spatiale, alors le champ électrique peut être obtenu à partir du gradient potentiel.

Le champ électrique est défini comme un vecteur, qui a une direction et une amplitude spécifiques. Lors de la détermination de la direction dans laquelle le potentiel électrique diminue plus rapidement - ce sera le point de référence - et en divisant cette valeur par la distance parcourue, l'ampleur du champ électrique est obtenue.

Caractéristiques du gradient potentiel

Le gradient potentiel est un vecteur délimité par des coordonnées spatiales spécifiques, qui mesure le rapport de changement entre le potentiel électrique et la distance parcourue par ledit potentiel. 

Les caractéristiques les plus remarquables du gradient de potentiel électrique sont détaillées ci-dessous:

1- Le gradient potentiel est un vecteur. Par conséquent, il a une magnitude et une direction spécifiques.

2- Étant donné que le gradient potentiel est un vecteur dans l'espace, il a des amplitudes dirigés dans les axes x (largeur), y (haut) et z, si le système de coordonnées cartésien est considéré comme une référence.

Peut vous servir: Système d'exploitation manquant: qu'est-ce que cela signifie et comment le résoudre

3- Ce vecteur est perpendiculaire à la surface de l'équipement au point auquel le potentiel électrique est évalué.

4- Le vecteur de gradient potentiel est dirigé vers la direction de la variation maximale de la fonction de potentiel électrique à tout moment.

5- Le module de gradient potentiel est égal à la dérivée de la fonction de potentiel électrique par rapport à la distance parcourue dans le sens de chacun des axes du système de coordonnées cartésiennes.

6- Le gradient potentiel a une valeur nulle aux points stationnaires (points maximum, minimum et chaise).

7- Dans le système des unités internationales (SI), les unités potentielles de mesure du gradient sont des volts / mètres.

8- La direction du champ électrique est la même dans laquelle le potentiel électrique diminue son ampleur plus rapidement. À son tour, le gradient potentiel pointe dans la direction dans laquelle le potentiel augmente sa valeur par rapport à un changement de position. Ensuite, le champ électrique a la même valeur du gradient potentiel, mais avec le signe opposé.

Comment le calculer?

La différence de potentiel électrique entre deux points (point 1 et point 2) est donnée par l'expression suivante:

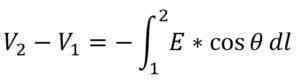
Où:

• V1: potentiel électrique au point 1.
• V2: potentiel électrique au point 2.
• E: amplitude du champ électrique.
• Ѳ: angle l'inclinaison du vecteur de champ électrique mesuré par rapport au système de coordonnées.

En exprimant cette formule différentiellement, ce qui suit suit:

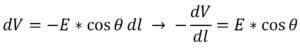
Le facteur e * cos (ѳ) fait référence au module du composant de champ électrique dans la direction de DL. Soit l l'axe horizontal du plan de référence, puis cos (ѳ) = 1, comme ceci:

Peut vous servir: technologie

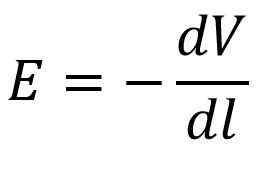
Ci-après, le quotient entre la variation du potentiel électrique (DV) et la variation de la distance parcourue (DS) est le module de gradient potentiel pour ledit composant. 

De là, il s'ensuit que l'ampleur du gradient de potentiel électrique est égale à la composante du champ électrique dans l'adresse de l'étude, mais avec le signe opposé.

Cependant, comme l'environnement réel est à trois dimensions, le gradient potentiel à un point donné doit être exprimé comme la somme de trois composants spatiaux dans les axes x et z du système cartésien.

Lorsque le vecteur de champ électrique se casse dans ses trois composants rectangulaires, vous avez ce qui suit:

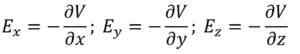
S'il y a une région dans le plan dans lequel le potentiel électrique a la même valeur, la dérivée partielle de ce paramètre par rapport à chacune des coordonnées cartésiennes sera nulle.

Ainsi, aux points de l'équipement, l'intensité du champ électrique aura une ampleur zéro.

Enfin, le vecteur de gradient potentiel peut être défini comme exactement le même vecteur de champ électrique (en amplitude), avec le signe opposé. Ainsi, vous avez ce qui suit:

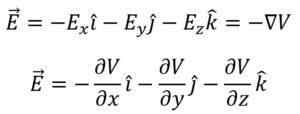
Exemple

D'après les calculs précédents, vous devez:

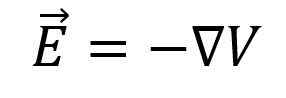
Cependant, avant de déterminer le champ électrique en fonction du gradient potentiel, ou vice versa, la direction dans laquelle la différence de potentiel électrique augmente doit être déterminée en premier.

Après cela, le quotient de la variation du potentiel électrique et la variation de la distance nette parcourue est déterminée.

De cette façon, l'ampleur du champ électrique associé est obtenue, ce qui est égal à l'ampleur du gradient potentiel en cette coordonnée.

Il peut vous servir: 23 avantages et inconvénients de l'étude en ligne

Exercer

Il y a deux plaques parallèles, comme en témoigne la figure suivante.

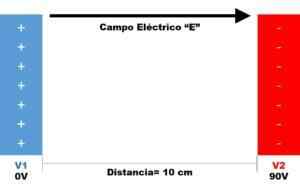
Étape 1

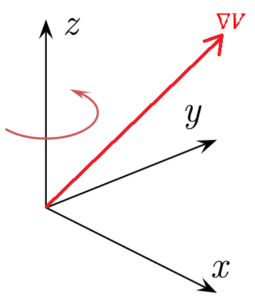
L'adresse de croissance du champ électrique sur le système de coordonnées cartésiennes est déterminée.

Le champ électrique ne pousse qu'en direction horizontale, étant donné la disposition des plaques parallèles. Par conséquent, il est possible de déduire que les composants du gradient potentiel sur l'axe y et l'axe z sont nuls.

Étape 2

Les données d'intérêt sont discriminées contre.

• Différence de potentiel: DV = V2 - V1 = 90 V - 0 V => DV = 90 V.
• Différence de distance: dx = 10 centimètres.

Pour garantir la congruence des unités de mesure utilisées selon le système international des unités, les amplitudes qui ne sont pas exprimées en elles-mêmes doivent être converties comme appropriées. Ainsi, 10 centimètres équivaut à 0,1 mètre, et enfin: dx = 0,1 m.

Étape 3

L'ampleur du vecteur de gradient potentiel est calculée comme approprié.