Fonctions mathématiques

Une fonction mathématique est la relation entre deux amplitudes, lorsque la première dépend du second. Volet

Quelles sont les fonctions mathématiques?

Le fonctions mathématiques Ils sont l'expression dans le langage mathématique d'une relation entre deux variables, et la valeur de la première des variables dépend du second. Normalement, ces variables sont symbolisées par les lettres x et y.  La variable x est appelée domaine ou variable indépendante; et au Y, codominium ou variable dépendante.

Regardons un exemple. Nous avons deux variables ou amplitudes: le dollar et les cents. Nous savons que 100 cents équivaut à un dollar. Par conséquent, les cents (x) sont le domaine et le dollar (y) correspond à la codominium. Cette relation peut être exprimée avec la fonction suivante (f):

F (x) = y / 100

Si j'ai 143 cents dans ma tirelire et que je veux savoir combien de dollars j'ai économisé, je n'applique que la fonction:

F (x) = 143/100

Par conséquent, j'ai 1,43 $.

Nous pouvons également exprimer la relation inverse, c'est-à-dire qu'un dollar équivaut à 100 cents. Par conséquent, les catégories des variables sont investies: le dollar (x) devient le domaine tandis que les cents sont le codominium. Nous l'exprimons de cette manière:

F (x) = x x 100

Si j'ai 1,43 $ dans ma tirelire, mais je veux savoir combien de cents ce chiffre est équivalent, il suffit d'appliquer cette deuxième fonction.

F (x): 1,43 x 100

Le résultat revient à mes 143 cents originaux.

Les variables des fonctions mathématiques

Une variable est simplement un symbole (x, y, z) qui représente une variété d'éléments.

Dans l'exemple précédent, les variables X et Y symbolisaient le dollar et le centime du dollar. Mais les mêmes symboles (x et y) peuvent être utilisés pour représenter une infinité d'éléments, tels que: l'âge d'une personne et leur poids; Nombre de vols vers une certaine destination et une période de temps (par semaine, par mois, par an), etc.

Peut vous servir: division synthétique

Les variables peuvent être classées en de nombreux types, mais les plus pertinentes pour les fonctions mathématiques sont les suivantes:

• Variable dépendante: Ceux dont la valeur dépend de la valeur attribuée à d'autres variables dans la fonction.
• Variable indépendante: Les changements dans ce type de variable influencent les valeurs du reste des variables de la fonction.
• Variable quantitative: Il est exprimé par des quantités numériques définies. Ils peuvent être des nombres entiers ou décimaux.

Caractéristiques des fonctions mathématiques

1- La relation entre les variables est exprimée en termes d'équivalence.

2- Pour chaque valeur de la variable x, il y a un, et seulement un équivalent de la variable et. Et vice versa: pour une certaine valeur de y, il y a un, et seulement un résultat de la variable x.

3- Ils peuvent être représentés graphiquement sur un plan cartésien, ce qui permet de prédire le comportement de l'une des variables de l'autre.

4- La définition moderne de la fonction mathématique est due au mathématicien allemand Peter Dirichlet (1805-1859), qui l'a publié en 1837.

Types de fonctions mathématiques

Les fonctions mathématiques peuvent être classées selon différents critères, tels que la relation établie entre les variables x et y o le comportement mathématique de la fonction.

Parmi les principaux types sont les suivants:

Fonctions algébriques

Ils se caractérisent en établissant une relation entre des composants exprimés soit par un monomial ou un polynôme. Cette relation peut être déterminée par des opérations mathématiques simples, telles que la soustraction, la multiplication, la division, la somme, la potentialisation ou la diffusion.

Fonctions linéaires

Lorsqu'ils sont représentés sur un plan cartésien, ils apparaissent avec la forme d'une ligne droite qui coupe l'axe de coordonnées à un certain point. D'où leur nom, bien qu'ils soient également connus sous le nom de fonctions de premier degré.

Peut vous servir: facteur commun: caractéristiques, exemples, exercices

Fonctions en morceaux

Dans ce type, la valeur du codominium et modifie le comportement de la fonction. Il y a donc deux intervalles avec un comportement différent par rapport à la valeur du domaine.

Fonctions transcendantes

Ce sont des fonctions très complexes. Les opérations algébriques courantes ne sont pas suffisantes (soustraction, multiplication, division, somme, potentialisation ou rayonnement) pour déterminer la relation entre les variables, de sorte que d'autres outils mathématiques doivent être utilisés, tels que les dérivés, les intégrales ou les logarithmes.

Fonctions trigonométriques

Ce type de fonctions montre la relation numérique qui existe entre les différents éléments d'un triangle et d'autres figures géométriques, en particulier parmi ses angles. Les formules pour le sein, le cosinus, la tangente, le secantique et Harmonte sont des exemples de ce type de fonctions.

Fonctions d'injectif

Les fonctions de ce type sont caractérisées par la particularité de la relation entre le domaine et la codominium. À chacune des valeurs de ce dernier une seule valeur de domaine correspond. Il peut également arriver qu'une valeur de domaine ne possède aucune valeur correspondante dans le codominium.

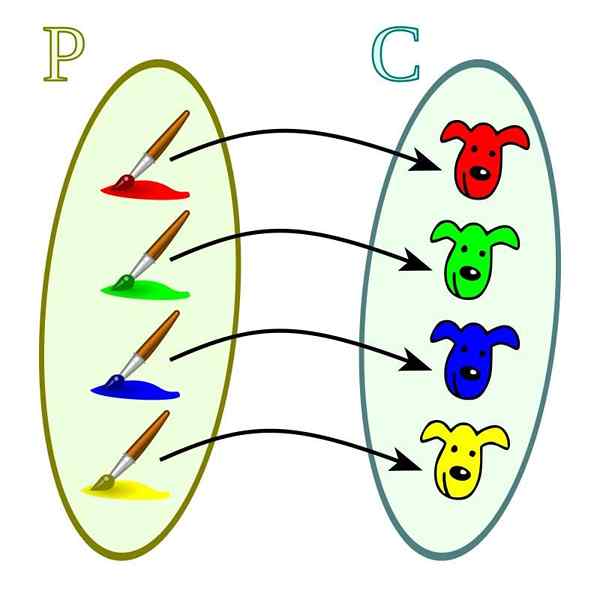Fonction d'injectif. Source: Wikimedia Commons

Fonctions onjectives

Dans ce cas, chacune des amplitudes de la codominium est liée à au moins une des valeurs du domaine. Ils se distinguent des fonctions d'injective dans lesquelles les valeurs de codominium peuvent être liées à plus d'une des valeurs de domaine.

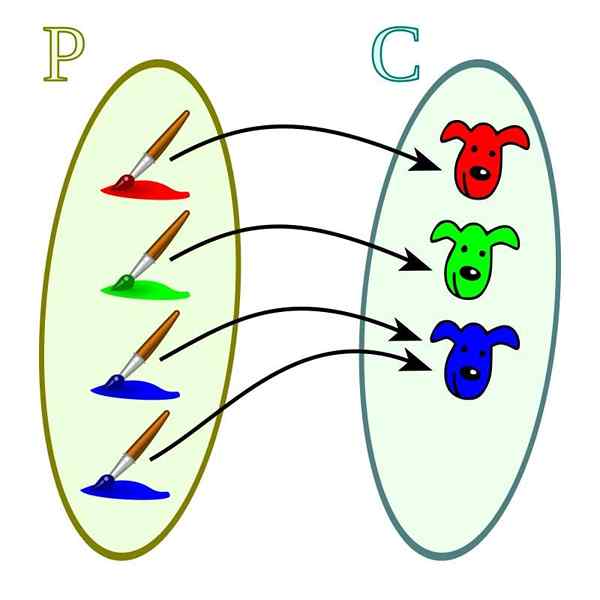Fonction de sur-objectif. Source: Wikimedia Commons

Fonctions bijectives

Ce type de fonctions présente à la fois des propriétés injectives et surcougées.

Quelles sont les fonctions mathématiques pour?

Les fonctions sont largement utilisées dans toutes les sciences qui ont des mathématiques en tant que science auxiliaire. C'est le cas de la physique, de l'ingénierie, de la médecine, de la finance, des statistiques, entre autres.

Peut vous servir: distribution de fréquence: comment faire un tableau, exemple, exercice

Dans la vie quotidienne

Cependant, nous pouvons également être utiles pour résoudre des problèmes quotidiens plus simples.

Imaginez que votre grand-père vous ait donné 10 pièces, que vous dépenserez en chocolat. Dans le kiosque, vous avez donné les 10 pièces à la personne à charge, lui disant de vous donner tous les chocolats qui peuvent être achetés avec cette quantité de devises. Ils vous ont donné 5 chocolats. Quel est le prix de chacun?

Nous proposons le problème: si 5 chocolats équivaut à 10 pièces, alors combien de pièces sont-elles équivalentes à un seul chocolat?

Notre variable indépendante (x) est la quantité de chocolats (5), tandis que la variable dépendante (Y) correspond au nombre de devises, c'est-à-dire 10.

Nous exprimons la fonction comme suit:

F (x) = 2x / x

F (x) = 2 (5) / 5

F (x) = 10/5

F (x) = 2

Et nous avons déjà la réponse: chaque chocolat coûte 2 pièces.

Les références

1. (S / F). Fonctions élémentaires. Le site des fonctions mathématiques. Pris des onctions.Wolfram.com.
2. (S / F). Qu'est-ce qu'une fonction? Tiré de Mathsisfun.com.