Propriétés de la fonction logarithmique, exemples, exercices

La fonction logarithmique C'est une relation mathématique qui associe chaque nombre réel positif X Avec votre logarithme et sur une base pour. Cette relation répond aux exigences pour être une fonction: chaque élément X appartenant au domaine a une image unique.

Donc:

f (x) = y = log_pour X , Avec un> 0 et différent de 1.

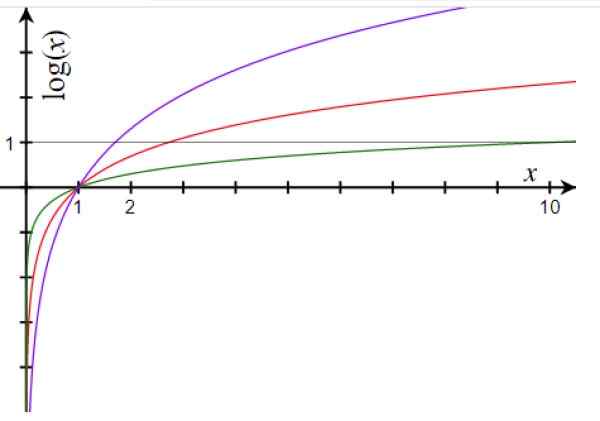
Figure 1. Graphique de fonction de logarithme pour la base 10 (vert), la base e (rouge) et la base 1.7 (violet). Source: Wikimedia Commons.

Les principales propriétés de la fonction logarithmique sont:

-Son domaine sont tous les Reais supérieurs à 0, sans compter 0. En d'autres termes, il n'y a pas de logarithme ou de nombres négatifs sur une base. Sous la forme d'un intervalle:

Soleil _F = (0, ∞ +)

-Le logarithme d'un nombre peut être négatif, positif ou 0, de sorte que sa gamme ou son itinéraire est:

Rgo _F = (-∞, ∞ +)

-La fonction logarithmique augmente toujours pour un> 1 et diminue<1.

-L'inverse de f (x) = journal_pour X est la fonction exponentielle.

En effet, la fonction de logarithme basée sur est la fonction inverse de la fonction potentielle:

F^-1(x) = a^et

Depuis le logarithme basé pour d'un nombre X, C'est le numéro et à laquelle la base doit être soulevée pour pour obtenir X.

-Le logarithme de base est toujours 1. Ainsi, le graphique de f (x) = journal_pour X Toujours se croiser à l'axe x au point (1.0)

-La fonction logarithmique est transcendant et ne peut pas être exprimé en polynôme ou comme un quotient. En plus du logarithme, ce groupe comprend des fonctions trigonométriques et exponentielles, entre autres.

[TOC]

Exemples

La fonction logarithmique peut être établie à travers différentes bases, mais les plus utilisées sont 10 et et, où et C'est le nombre d'Euler égal à 2 71828 .. .

Lorsque la base 10 est utilisée, le logarithme est appelé logarithme décimal, logarithme vulgaire, Briggs ou simplement le logarithme à sécher.

Et si le numéro E est utilisé, alors il s'appelle Neperian Logarithme, par John Napier, le mathématicien écossais qui a découvert les logarithmes.

Peut vous servir: inverse multiplicatif: explication, exemples, exercices résolus

La notation utilisée pour chacune est la suivante:

-Logarithme décimal: journal_dix x = log x

-Logarithme népérienne: ln x

Quand une autre base va être utilisée, c'est absolument nécessaire. Par exemple, s'il s'agit de logarithmes sur la base 2, il est écrit:

y = journal₂ X

Regardons le logarithme numéro 10 en trois bases différentes, pour illustrer ce point:

Log 10 = 1

ln 10 = 2.30259

enregistrer₂ 10 = 3.32193

Les calculatrices communes n'apportent que des logarithmes décimaux (log) et un logarithme néérien (fonction LN). Sur Internet, il y a des calculatrices avec d'autres bases. Dans tous les cas, le lecteur peut vérifier, avec l'aide de ceux-ci, qu'avec les valeurs précédentes, elle est remplie:

dix¹ = 10

et^2.3026 = 10.0001

2^3.32193 = 10.0000

De petites différences décimales sont dues à la quantité de décimales prises dans le calcul du logarithme.

Les avantages des logarithmes

Parmi les avantages de l'utilisation des logarithmes est la facilité qu'ils offrent pour travailler avec de grands nombres, en utilisant leur logarithme au lieu du nombre directement.

Cela est possible car la fonction de logarithme se développe plus lentement car les nombres sont plus importants, comme nous l'apprécions dans les graphiques.

Ainsi, même dans le cas de très grands nombres, leurs logarithmes sont beaucoup plus petits et manipuler les petits nombres est toujours plus facile.

De plus, les logarithmes répondent aux propriétés suivantes:

-Produit: Log (A.b) = log a + log b

-Quotient: log (a / b) = log a - log b

-Pouvoir: log A^b = b.enregistrer un

Et de cette manière, les produits et quotients deviennent des sommes et de la soustraction de plus petits nombres, tandis que la potentialisation est transformée en un produit simple bien que la puissance soit élevée.

C'est pourquoi les logarithmes permettent d'exprimer des nombres qui varient en très grandes gammes de valeurs, telles que l'intensité du son, le pH d'une solution, la luminosité des étoiles, la résistance électrique et l'intensité des tremblements de terre sur le Richter escalader.

Peut vous servir: angles alternatifs externes: exercices et exercices résolusFigure 2. Les logarithmes sont utilisés sur l'échelle Richter pour quantifier l'ampleur des tremblements de terre. L'image montre un bâtiment effondré à Concepción, au Chili, pendant le tremblement de terre de 2010. Source: Wikimedia Commons.

Regardons un exemple de la gestion des propriétés des logarithmes:

Exemple

Trouvez la valeur de x dans l'expression suivante:

log (5x +1) = 1 + log (2x-1)

Répondre

Nous avons ici une équation logarithmique, compte tenu du fait que l'inconnu est sur l'argument du logarithme. Il est résolu en laissant un seul logarithme de chaque côté de l'égalité.

Nous commençons par placer tous les termes qui contiennent "x" à gauche de l'égalité, et ceux qui ne contiennent que des nombres à droite:

log (5x + 1) - log (2x -1) = 1

À gauche, nous avons la soustraction de deux logarithmes, qui peuvent être écrits comme le logarithme d'un quotient:

log [(5x + 1) / (2x-1)] = 1

Cependant, à droite est le numéro 1, que nous pouvons exprimer en tant que journal 10, comme nous l'avons vu précédemment. Ensuite:

log [(5x + 1) / (2x-1)] = log 10

Pour que l'égalité soit remplie, le arguments des logarithmes doivent être les mêmes:

(5x + 1) / (2x-1) = 10

5x + 1 = 10 (2x - 1)

5x + 1 = 20 x - 10

-15 x = -11

x = 11/15

Exercice d'application: l'échelle de Richter

En 1957, un tremblement de terre s'est produit au Mexique dont l'ampleur était de 7.7 sur l'échelle Richter. En 1960, un autre tremblement de terre de plus grande ampleur s'est produit au Chili, 9.5.

Calculez combien de fois le tremblement de terre chilien était plus intense que celui du Mexique, sachant que l'ampleur m_R Sur l'échelle de Richter, il est donné par la formule:

M_R = log (10⁴ Yo)

Solution

L'ampleur de l'échelle de Richter d'un tremblement de terre est une fonction logarithmique. Nous allons calculer l'intensité de chaque tremblement de terre, car nous avons les amplitudes Richter. Faisons-le pas à pas:

Peut vous servir: Nombres primo: caractéristiques, exemples, exercices

-Mexique: 7.7 = log (10⁴ Yo)

Comme l'inverse de la fonction de logarithme est l'exponentiel, nous appliquons cela des deux côtés de l'égalité avec l'intention de nettoyer I, qui se trouve dans l'argument du logarithme.

Puisqu'ils sont des logarithmes décimaux, la base est de 10. Ensuite:

Dans le terme de droite, 10 et log (10⁴ I) Ils sont annulés (comme avec la racine carrée et carrée), étant: partant:

dix ^7.7 = 10⁴ Toi

L'intensité du tremblement de terre du Mexique était:

Toi_M = 10 ^7.7 / dix⁴ = 10^3.7

 -le Chili: 9.5 = log (10⁴ Yo)

La même procédure nous amène à l'intensité du tremblement de terre chilien i_Ch:

Toi_Ch = 10 ^9.5 / dix⁴ = 10^5.5

 Nous pouvons maintenant comparer les deux intensités:

Toi_Ch / Yo_M = 10^5.5 / dix^3.7 = 10^1.8 = 63.1

 Toi_Ch = 63.1. Toi_M

Le tremblement de terre du Chili était environ 63 fois plus intense que le Mexique. Comme l'ampleur est logarithmique, elle se développe plus lentement que l'intensité, donc une différence de 1 amplitude signifie une amplitude 10 fois plus élevée de l'onde sismique.

La différence entre les amplitudes des deux tremblements de terre est 1.8, par conséquent, nous pourrions nous attendre à une différence d'intensités plus proche de 100 que de 10, comme cela s'est produit efficacement.

En fait, si la différence avait été 2 exactement, le tremblement de terre chilien aurait été 100 fois plus intense que le mexicain.

Les références

1. Carena, m. 2019. Manuel des mathématiques de préunité. Université nationale de la côte.
2. Figuera, J. 2000. Mathématiques 1er. Année diversifiée. Éditions co-bo.
3. Jiménez, R. 2008. Algèbre. Prentice Hall.
4. Larson, R. 2010. Calcul d'une variable. 9na. Édition. McGraw Hill.
5. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.