Fonction des caractéristiques constantes, exemples, exercices

La fonction constante C'est celui dans lequel la valeur de et. En d'autres termes: une fonction constante a toujours la forme  f (x) = k, où k C'est un vrai nombre.

En graphiquement la fonction constante dans le système de coordonnées Xy, C'est toujours une ligne droite parallèle à l'axe ou à l'axe horizontal de la X.

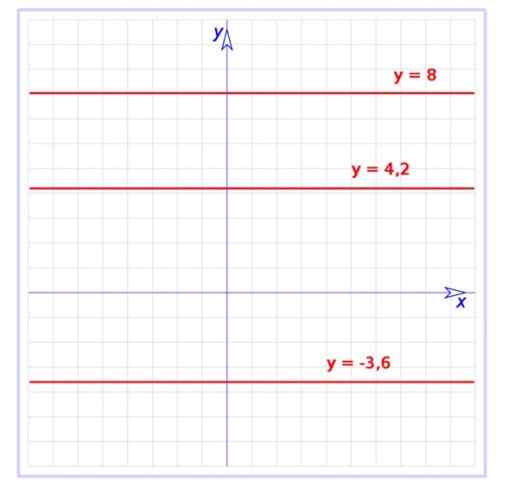
Figure 1. Graphique de plusieurs fonctions constantes sur le plan cartésien. Source: Wikimedia Commons. Utilisateur: Hite [domaine public]

Cette fonction est un cas particulier de la fonction connexe, dont le graphique est également une ligne droite, mais avec une pente. La fonction constante a une attente nulle, c'est-à-dire qu'il s'agit d'une ligne horizontale, comme le montre la figure 1.

Il y a le graphique de trois fonctions constantes:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Tous sont directement parallèles à l'axe horizontal, le premier est en dessous de cet axe, tandis que les autres sont au-dessus.

[TOC]

Caractéristiques de la fonction constante

Nous pouvons résumer les principales caractéristiques de la fonction constante comme suit:

-Son graphique est une ligne droite horizontale.

-Il a une intersection unique avec l'axe et, valeur k.

-C'est continu.

-La maîtrise de la fonction constante (l'ensemble de valeurs X) est l'ensemble des nombres réels R.

-L'itinéraire, la plage ou la contradiction (l'ensemble des valeurs que la variable prend et) est simplement la constante k.

Exemples

Les fonctions sont nécessaires pour établir des liens entre les amplitudes qui dépendent les uns des autres d'une manière ou d'une autre. La relation existante entre eux peut être modélisée mathématiquement, pour savoir comment l'un d'eux se comporte lorsque l'autre varie.

Peut vous servir: Papomudas

Cela aide à construire des modèles pour de nombreuses situations et à faire des prédictions sur leur comportement et leur évolution.

Malgré sa simplicité apparente, la fonction constante a de nombreuses applications. Par exemple, quand il s'agit d'étudier les amplitudes qui restent constantes dans le temps, ou du moins, pour un moment appréciable.

De cette façon, les amplitudes se comportent dans des situations telles que les suivantes:

-La vitesse Croisière d'une voiture qui se déplace sur une longue autoroute rectiligne. Tant qu'il ne s'arrête pas ou n'accélère pas, la voiture porte un mouvement rectiligne uniforme.

Figure 2. Si la voiture ne s'arrête pas ou ne s'accélère pas, elle a un mouvement rectiligne uniforme. Source: Pixabay.

-Un condenseur entièrement chargé et déconnecté d'un circuit, a un fardeau constant dans le temps.

-Enfin, un parking à taux forfaitaire, maintient un prix constant peu importe combien de temps une voiture y est garée.

Une autre façon de représenter une fonction constante

La fonction constante peut alternativement peut être représentée comme suit:

f (x) = kx⁰

Depuis toute valeur de X Soulevé à 0 donne 1 en conséquence, l'expression précédente est réduite au familier:

f (x) = k

Bien sûr, cela se produit aussi longtemps que la valeur de k est différent de 0.

C'est pourquoi la fonction constante est également classée comme un fonction polynomiale grade 0, depuis l'exposant de la variable X C'est 0.

Exercices résolus

- Exercice 1

Répondre aux questions suivantes:

A) peut-on affirmer que la ligne donnée par x = 4 est une fonction constante? Raison que votre réponse.

b) Une fonction constante peut-elle avoir l'intersection avec l'axe x?

c) est la fonction f (x) = w constant²?

Réponds à

Voici le graphique de la ligne x = 4:

Peut vous servir: variables statistiques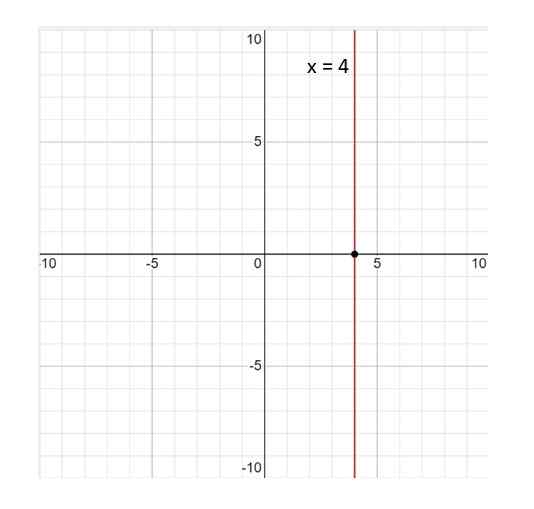 figure 3. Graphique de la ligne x = 4. Source: F. Zapata.

La ligne x = 4 n'est pas une fonction; Par définition, une fonction est une relation telle qu'à chaque valeur de la variable X Il correspond à une seule valeur de et. Et dans ce cas, ce n'est pas rempli, car la valeur x = 4 est associé à des valeurs infinies de et. Par conséquent, la réponse n'est pas.

Réponse b

En général, une fonction constante n'a pas d'intersection avec l'axe X, à moins que ce ne soit y = 0, Dans ce cas, c'est l'axe X Correctement dit.

Réponse C

Oui, depuis W C'est constant, son carré est aussi. Quels intérêts c'est que W Il ne dépend pas de la variable d'entrée X.

- Exercice 2

Trouver l'intersection entre les fonctions f (x) = 5 et G (x) = 5x - 2

Solution

Pour trouver l'intersection entre ces deux fonctions, ils peuvent être réécrits respectivement comme:

y = 5; y = 5x - 2

Ils sont appariés, obtenant:

5x - 2 = 5

Qui est une équation linéaire au premier degré, dont la solution est:

5x = 5 + 2 = 7

x = 7/5

Le point d'intersection est (7/5; 5).

- Exercice 3

Démontrer que celui dérivé d'une fonction constante est 0.

Solution

D'après la définition du dérivé que vous avez:

 f (x) = k

f (x + h) = k

Remplacement de la définition:

Ce qui précède a du sens, car la dérivée d'une fonction est définie comme la pente de la ligne tangente à la courbe à un point donné. La fonction constante a une attente nulle et toute ligne tangente aussi.

De plus, si nous considérons le dérivé comme un taux de change Dy / dx, La fonction constante ne subit aucun changement, donc son dérivé est vide.

Peut vous servir: Principe multiplicatif: techniques de comptage et exemples

- Exercice 4

Trouver l'intégrale indéfinie de f (x) = k.

Solution

- Exercice 5

Une société de téléphone portable propose un service Internet illimité avec un tarif forfaitaire payant 15 $ par mois. Quelle est la fonction de prix en fonction du temps?

Solution

Soit P le prix à payer à Time et T $, qui peut être exprimé en jours. La fonction est établie comme suit:

P (t) = 15

- Exercice 6

Le graphique de temps suivant correspond au mouvement d'une particule.

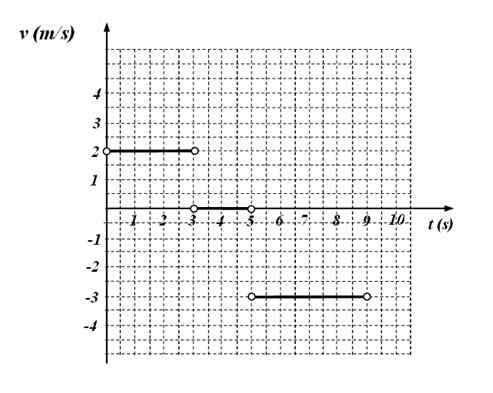Figure 4. Fonction V (T) Graphique de la fonction pour l'exercice 6. Source: F. Zapata.

On demande:

a) Écrivez une fonction d'expression pour la vitesse en fonction du temps V (t).

b) Trouvez la distance parcourue par le mobile dans l'intervalle de temps entre 0 et 9 secondes.

Solution à

Du graphique montrant que:

-V = 2 m / s Dans l'intervalle de temps entre 0 et 3 secondes

-Le mobile est détenu entre 3 et 5 secondes, car dans cet intervalle, la vitesse vaut 0.

-V = - 3 m / s Entre 5 et 9 secondes.

Il s'agit d'un exemple de morceaux de morceaux, ou de fonction en parties, qui à son tour sont composées de fonctions constantes, valides uniquement pour les intervalles de temps indiqués. Il est conclu que la fonction recherchée est:

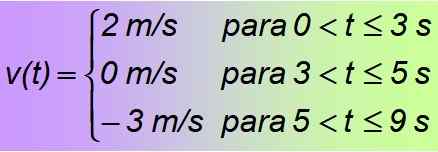
Solution B

À partir du graphique V (T), la distance parcourue par le mobile peut être calculée, ce qui est numériquement égal à la zone bas / sur la courbe. De cette manière:

-Distance parcourue entre 0 et 3 secondes = 2 m / s . 3 s = 6 m

-Entre 3 et 5 secondes, il a été détenu, donc il n'a parcouru aucune distance.

-Distance parcourue entre 5 et 9 secondes = 3 m / s . 4 s = 12 m

Au total, le mobile a tourné 18 m. Voyez que bien que la vitesse soit négative dans l'intervalle entre 5 et 9 secondes, la distance parcourue est positive. Ce qui se passe, c'est que pendant cet intervalle de temps, le mobile avait changé la signification de sa vitesse.

Les références

1. Géogebra. Fonctions constantes. Récupéré de: Geogebra.org.
2. Maplesoft. La fonction constante. Récupéré de: Maplesoft.com.
3. Wikilibros. Calcul dans une variable / fonctions / fonction constante. Récupéré de: est.Wikibooks.org.
4. Wikipédia. Fonction constante. Récupéré de: dans.Wikipédia.org
5. Wikipédia. Fonction constante. Récupéré de: est.Wikipédia.org.