Formule générale Équations quadratiques, exemples, exercices

La Formule générale, qui est également connu comme le formule de solvant Dans certains textes, il est utilisé pour résoudre les équations du deuxième degré: hache² + bx + c = 0.

En eux pour, b et c Ce sont des nombres réels, avec la condition que pour est différent de 0, être X L'inconnu. Ensuite, la formule générale présente la clairance de l'inconnu par une expression qui implique les valeurs de pour, b et c de la manière suivante:

Figure 1. La formule générale en mathématiques est utilisée pour résoudre les équations quadratiques. Source: F. Zapata.

Et à travers cette formule, vous pouvez trouver la solution de toute équation du deuxième degré ou quadratique, à condition que cette solution existe.

Selon les historiens, la formule générale était déjà connue des anciens mathématiques babyloniennes. Il a ensuite été transmis à d'autres peuples, comme les Égyptiens et les Grecs, par le biais d'échanges culturels.

La formule et ses variantes sont arrivées en Europe grâce aux mathématiciens musulmans installés dans la péninsule ibérique. Cependant, ils n'ont pas utilisé la notation algébrique que nous utilisons actuellement. Cette notation est due au mathématicien français et à l'expert cryptographique du XVIe siècle François Viete.

[TOC]

Équations quadratiques par la formule générale

Voyons comment la formule générale survient, afin de vérifier sa validité. À partir d'une équation quadratique générale:

hache² + bx + c = 0

Mettons en pratique des manipulations algébriques simples pour réaliser l'autorisation de l'inconnu. Il existe plusieurs façons de transporter cela, par exemple en terminant des carrés, comme illustré alors.

Démonstration de la formule générale

Nous commençons par ajouter (-c) des deux côtés de l'égalité:

hache² + Bx = - c

Et maintenant, il est multiplié par 4a, toujours des deux côtés de l'égalité, afin de ne pas modifier l'expression:

4e² X² + 4AB x = - 4AC

Ajout de b²:

4e²⋅X² + 4Ab⋅X + B² = - 4AC + B²

Le but de cela est de compléter les carrés du côté gauche de l'égalité, qui contient l'inconnu, de cette manière, son autorisation est facilitée. De cette façon:

Peut vous servir: Diviseurs de 8: Quelles sont les explications faciles

-Le premier terme: 4e² X² C'est le carré parfait de 2ax

-Le dernier, qui est b², C'est le carré parfait de b.

-Et le terme central est le double produit de 2ax et b: 2⋅2ax⋅b = 4abx

Par conséquent, nous avons un binôme carré:

4e²⋅X² + 4Ab⋅X + B² = (2ax + b)²

Et nous pouvons écrire:

(2ax + b)² = - 4AC + B²

Nous sommes à un pas de l'élimination de l'inconnu X:

Et nous obtenons déjà la formule générale que nous connaissons:

Il existe d'autres moyens de manipuler algébriquement l'équation quadratique et d'obtenir ce même résultat.

Exemples d'utilisation de la formule générale

Pour appliquer la formule générale, les valeurs de A, B et C sont soigneusement déterminées et remplacées dans la formule. Notez le symbole plus moins dans le numérateur; Cela indique que nous devons considérer deux possibilités concernant l'opération, une avec le signe + et une avec le signe -.

L'équation quadratique peut avoir les solutions suivantes, selon la valeur de la quantité sous-radicale, connue sous le nom discriminant:

-Oui B² - 4AC> 0, l'équation quadratique a deux solutions réelles et différentes.

-Quand b² - 4AC = 0, l'équation a une solution unique, donnée par:

x = -b / 2a

-Enfin, si b² - 4AC < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Examinons quelques exemples dans lesquels la formule générale est appliquée, remarquant que si l'un des coefficients qui accompagnent l'inconnu n'apparaît pas, il est entendu qu'il vaut 1. Et si le terme indépendant est celui qui n'est pas trouvé, alors il vaut 0.

- Exemple 1

Résolvez les équations quadratiques suivantes:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Réponds à

Nous écrivons les coefficients de chaque terme: a = 6, b = 11, c = -10 et remplaçant les valeurs dans la formule générale:

Peut vous servir: taxer

x = (-11 ± 19) / 12

Le résultat conduit aux deux vraies solutions suivantes:

X₁ = (-11 + 19) / 12 = 8/12 = 2/3

X₂ = (-11 -19) / 12 = -5/2

Réponse b

Encore une fois, les coefficients sont déterminés: a = 3, b = -5 et c = -1. En remplaçant dans la formule:

Contrairement au cas précédent, la racine carrée de 37 n'est pas un entier, mais nous pouvons également élever les deux solutions et laisser la racine ou trouver la valeur décimale correspondante à l'aide de la calculatrice:

X₁ = (-5 + √37) / 6 ≈ 0.18

X₂ = (-5 - √37) / 6 ≈ - 1.85

- Exemple 2

Résoudre l'équation du deuxième degré x² - 4x +13 = 0.

Répondre

Comme toujours, nous identifions les valeurs des coefficients et remplaçons la formule générale: a = 1, b = - 4, c = 13. Cela mène à:

Nous avons une racine négative, donc les solutions de cette équation sont des nombres complexes. La racine peut être exprimée en termes de Toi, la Unité imaginaire:

√ (36i²) = 6i

Depuis que je² = -1, donc les solutions complexes sont:

X₁ = (4 + 6i) / 2 = 2 + 3i

X₂ = (4 - 6i) / 2 = 2 - 3i

Exercice résolu

Un escalier de 10 m de long repose contre un mur vertical, avec le pied à 6 m de ce mur. L'escalier se glisse et le pied est séparé de 3 m de plus de la base.

Trouvez la distance verticale qui traverse le haut de l'escalier.

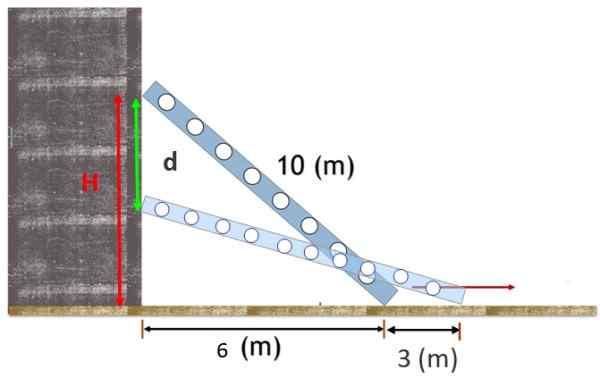Figure 2. Un escalier soutenu sur un mur glisse un peu et l'arrêt supérieur se déplace verticalement sur une distance d. Source: F. Zapata.

Solution

Pour trouver la distance verticale qui glisse le haut de l'escalier, vous devez trouver la position dans laquelle elle était à l'origine en ce qui concerne le sol. Nous pouvons le faire avec le théorème de Pythagore, car la figure qui est formée est celle d'un triangle droit:

H = (10² - 6²) ^½ = 8 m

Une fois l'escalier glisser, une distance se déplace d, Mesurer puisque le haut mesurait 8 m de haut, jusqu'à ce qu'il atteigne sa nouvelle position, à (H-D) mètres au-dessus du sol. L'inconnu à Clear est D.

Peut vous servir: fréquence accumulée: formule, calcul, distribution, exemples

Pour le trouver, nous proposons un nouveau triangle rectangle, qui est formé après que l'échelle a glissé un peu. Ce triangle a encore une hypotenusa égale à 10 m et le Cateto parallèle est maintenant de 6 m + 3 m = 9 m, donc:

(HAUTE DÉFINITION)² = 10² - 9² = 100 - 81 = 19

Nous remplaçons h = 8m, précédemment calculé:

(8-D)² = 19

L'équation peut être résolue de plusieurs manières, y compris l'utilisation de la formule générale, que nous montrerons ci-dessous avec ces étapes:

Étape 1

Développer la gauche notable de la gauche:

64 -16d + d² = 19

Étape 2

Établir l'équation du deuxième degré pour l'inconnu d:

d² - 16d + 45 = 0

Étape 3

-Les coefficients sont: a = 1, b = -16 et c = 45, nous les remplaçons dans la formule générale:

Les solutions de l'équation sont:

d₁ = (16 + √76) / 2 ≈ 12.36 m

d₂ = (16 - √76) / 2 ≈ 3.64 m

Étape 4

Les solutions obtenues sont analysées: la première n'a pas de sens physique, car il n'est pas possible pour l'échelle de compiler 12.36 m, si à l'origine l'arrêt était de 8 m de haut sur le sol.

Par conséquent, la bonne réponse est la deuxième solution: le haut de l'escalier glisse D = 3.64 m.

Le lecteur peut-il résoudre le problème en appliquant une autre méthode?

Les références

1. Baldor. 1977. Algèbre élémentaire. Éditions culturelles vénézuéliennes.
2. Hoffman, J. Sélection de problèmes de mathématiques. 2ieme volume.
3. Jiménez, R. 2008. Algèbre. Prentice Hall.
4. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
5. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.