Caractéristiques des facteurs communs, exemples, exercices

Il facteur commun d'une expression algébrique est une quantité qui est présente dans tous les termes de ce. Lorsque le facteur commun est connu, il est possible d'écrire l'expression de manière équivalente à travers un produit de facteurs.

Toutes les expressions algébriques n'ont pas un facteur commun, il n'y a que ceux qui ne peuvent être divisés entre eux et 1, il n'est donc pas possible de les écrire comme produit de facteurs. Un exemple d'expression qui n'a aucun facteur commun est:

x + y

Figure 1. Le facteur commun d'une expression algébrique en fait le produit indiqué de deux facteurs. Source: Pixabay.

Au lieu de cela oui:

5a + 10b

On voit que le 5 est présent dans les deux termes, depuis 10 = 5 ∙ 2. Puisque 5 est le facteur commun, alors les éléments suivants peuvent être écrits:

5a + 10b = 5 ∙ (A + 2B)

Le lecteur peut vérifier à travers une propriété distributive, que l'expression à droite est égale à l'original.

Le facteur commun peut également être littéral ou une combinaison de nombres et de lettres, par exemple dans 4x² - 2x. La X et le 2 Ils sont entre les facteurs et l'expression reste un produit:

4x² - 2x = 2x⋅ (x - 1)

L'avantage de trouver le facteur commun d'une expression et de l'écrire en tant que produit est qu'il est presque toujours facile de fonctionner avec lui. C'est pourquoi il est utilisé dans de nombreuses procédures algébriques et de calcul telles que:

-Lors de la résolution des équations, dont les solutions sont rapidement révélées lorsque le facteur commun est trouvé.

-Lors du calcul d'une limite avec une indétermination, cela peut disparaître en tenant correctement.

-La factorisation appropriée facilite également les opérations avec des expressions algébriques rationnelles, telles que les sommes et les soustractions.

[TOC]

Caractéristiques du facteur commun

Les principales caractéristiques du facteur commun sont les suivantes:

-Il peut s'agir d'un nombre, d'une expression algébrique ou d'une combinaison des deux.

-Le facteur commun doit être contenu dans chacun des termes de l'expression de facteur.

Peut vous servir: fonctions transcendantes: types, définition, propriétés, exemples

-Selon le montant des conditions qu'il contient, il se peut que ce soit:

1. Facteur monomial commun, si le facteur commun est d'un seul terme,
2. Facteur binomial commun si vous avez deux termes et
3. Facteur polynomial commun, si le facteur commun se compose de plusieurs termes.

Comment trouver le facteur commun d'une expression algébrique?

Pour trouver le facteur commun présent dans un polynôme, vous devez calculer le diviseur ou le MCD commun maximum des coefficients numériques de tous les termes, ainsi que les lettres ou littéraux de chaque terme et choisissez la puissance avec le moindre exposant.

Les lettres ou littéraux peuvent être présentés sous forme de monomiaux, de binômes ou de polynômes, comme on le verra dans les exemples suivants.

Le plus recommandé pour comprendre le processus d'obtention du facteur commun, est de suivre les exemples et de pratiquer la résolution de plusieurs exercices dans chaque cas.

Exemples de facteurs communs

Nous ne devons pas perdre de vue le fait que l'objectif de facteur commun est converti une expression en un produit indiqué de facteurs. Ensuite, les cas les plus pertinents sont analysés:

Facteur monomial commun

Vous avez les monomiaux suivants (expressions algébriques à un seul terme):

2x²; 10x⁴et; 100x⁶et²

Quel peut être le facteur commun pour les trois?

En commençant par les coefficients numériques: 2, 10 et 100, tous sont uniformes et leur MCD est 2. Quant à la partie littérale, la variable x est présente dans les trois termes, et la puissance la plus basse est x², Alors le facteur commun est 2x².

Les trois termes proposés peuvent être écrits comme des produits de ce facteur de cette manière:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²et

100x⁶et²= 2x²∙ 50X⁴et²

Multipliant les facteurs à droite, il peut être vérifié que le terme de gauche est obtenu.

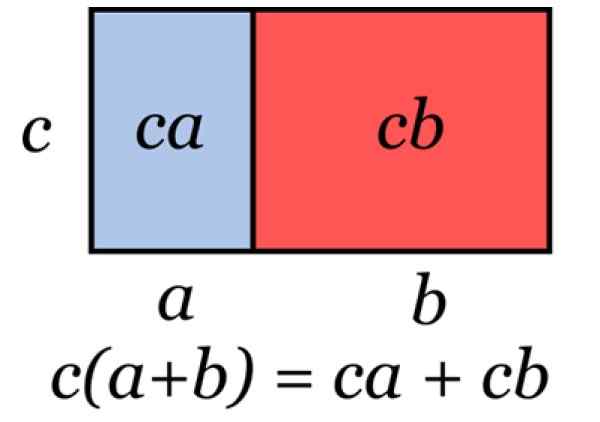Figure 2. Illustration qui représente le facteur commun. Source: Wikimedia Commons.

Cette technique est appliquée lorsqu'elle est nécessaire pour prendre en compte une expression algébrique, comme dans les exemples suivants:

• Exemple 1

Fait l'expression suivante:

Il peut vous servir: triangle isocèle

5x³et + 10x²et² + 5xy²

Le MCD des coefficients numériques de chaque terme est:

MCD (5.10) = 5

Quant à la partie littérale, les deux X comme la et Ils sont présents dans les trois termes et le moins d'exposant de chacun est 1, donc le facteur commun est 5xy Et vous pouvez écrire:

5x³et + 10x²et² + 5xy²= 5xy ∙ (x² +2xy²+et)

Facteur polynomial commun

Le facteur commun peut être constitué d'un binôme, d'un trinomial ou en général dans un polynôme. Dans ce cas, les instructions de la section précédente sont toujours valides, choisissant comme facteur commun celui avec le moindre exposant.

• Exemple 2

Écrivez l'expression suivante comme produit de deux facteurs:

2a (x - 1) - 3b (x - 1)

Par inspection directe, le facteur commun est le binomial (X-1), ensuite:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2a - 3b)

Factorisation en regroupant les termes

Parfois, l'existence d'un facteur commun n'est pas évidente, mais il est révélé si les termes sont regroupés de manière pratique:

• Exemple 3

Factoriser 3x³ - 9ax² - x + 3a

À première vue, il n'y a aucun facteur commun dans ces quatre termes, car par exemple le X Il est présent dans les trois premiers, mais pas dans le dernier. Et la pour C'est dans le deuxième et dans le dernier rien de plus.

Quant aux coefficients, il y a trois termes dans lesquels le 3 est présent, cependant pour être un facteur commun, il devrait être en tous termes.

Il semble que les techniques décrites ne peuvent pas être appliquées cette fois. Cependant, l'expression peut être en tenant compte en regroupant les deux premiers termes et les deux derniers, en étant prudent lors de la mise en place de la parenthèse, que les signes sont appropriés pour ne pas modifier l'original:

Peut vous servir: composants rectangulaires d'un vecteur (avec des exercices)

3x³ - 9ax² - x + 3a = (3x³ - 9ax²) - (x - 3a)

Notez le signe négatif au milieu des parenthèses: c'est nécessaire, car sinon l'expression originale changerait.

Dans la parenthèse gauche, le facteur commun est 3x², donc:

(3x³ - 9ax²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

Et il est observé qu'un facteur commun est déjà apparu: (x - 3a), C'est-à-dire qu'il est facteur pour la deuxième fois d'obtenir:

3x² (X- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Exercices de facteur commun

Exercice 1

Résoudre l'équation 4x³ +7x²  +6x = 0

Solution

"X" est donc un facteur commun:

3x³ -5x²  +2x = x (3x² −5x +2) = 0

Pour l'expression à gauche, c'est 0, il suffit que l'une de ces deux conditions soit remplie:

x = 0

SOIT:

3x² −5x +2 = 0

Il s'agit d'une équation complète du deuxième degré qui peut être résolue en appliquant la formule générale, également en utilisant une calculatrice scientifique ou une autre méthode algébrique. Les solutions de cette équation sont:

x = 1

x = 2/3

Une fois trouvé, il est illustratif d'écrire l'équation comme le produit de 3 facteurs, bien que la déclaration ne l'ait pas demandé. Ce serait comme ceci:

x⋅ (x-1) ⋅ (x-2/3) = 0

Exercice 2

Calculez la limite suivante si elle existe:

Solution

Il est d'abord remplacé à x = −2 pour essayer d'évaluer la limite, ce faisant, il est obtenu:

Comme il s'agit d'une indétermination de la forme 0/0, vous devez être facteur pour essayer de l'éliminer. Le dénominateur ne peut pas être facteur, mais le numérateur.

Dans le numérateur, le facteur commun est X:

X²+2x = x ∙ (x + 2)

L'expression factorielle est remplacée dans la limite et de cette manière l'indétermination disparaît:

Il est conclu que la limite existe et vaut −2.

Les références

1. Baldor, un. 2005. Algèbre. Groupe de patrie culturelle.
2. Jiménez, R. 2008. Algèbre. Prentice Hall.
3. Larson, R. 2012. Précalation. 8e. Édition. Cengage Learning.
4. Stewart, J. 2007. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
5. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.