Effort normal de quoi il s'agit, comment il est calculé, exemples

Il effort normal Appliqué à un certain matériau, également appelé effort uniaxial, c'est la relation entre la force appliquée perpendiculaire à une certaine surface et la zone de section transversale sur laquelle elle agit, ou la charge par unité de surface. Mathématiquement, si P est l'ampleur de la force et a est la zone où elle est appliquée, l'effort σ est le quotient: σ = p / a.

Les unités d'effort normal dans le système international sont Newton / Metro², connu sous le nom de Pascal et abrégé PA. Ce sont les mêmes unités de pression. D'autres unités qui apparaissent dans la littérature sont fréquemment des livres / pouces² soit psi.

Figure 1. Les roches sont constamment soumises à des efforts dus à une activité tectonique, provoquant des déformations dans la croûte terrestre. Source: Pixabay.

Dans la figure 2.

Ces forces produisent un effort normal qui est également appelé Charge axiale centré, car sa ligne d'action coïncide avec l'axe axial, sur lequel se trouve le centroïde.

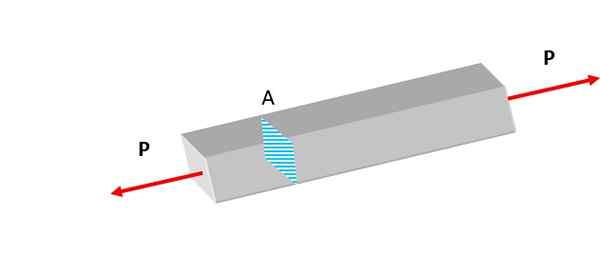Figure 2. La barre montrée est soumise à des forces de traction. Source: auto-faite.

Les efforts, qu'ils soient normaux ou autres, apparaissent en continu dans la nature. Dans la lithosphère, les roches sont soumises à la gravité et à l'activité tectonique, expérimentant les déformations.

De cette façon, des structures telles que les plis et les échecs sont originaires, dont l'étude est importante dans l'utilisation des minéraux et du génie civil, pour la construction de bâtiments et de routes, pour nommer quelques exemples.

[TOC]

Comment est-il calculé?

L'équation donnée au début σ = p / a permet de calculer l'effort normal moyen sur la zone en question. La valeur de P est l'ampleur de la force résultante sur la zone appliquée au centroïde et est suffisante pour de nombreuses situations simples.

Dans ce cas, la distribution des forces est uniforme, en particulier à des points loin de l'endroit où vous avez la barre soumise à une traction ou à une compression. Mais si l'effort est nécessaire pour calculer à un point spécifique ou si les forces ne sont pas réparties uniformément, il est nécessaire d'utiliser la définition suivante:

Peut vous servir: circuit électrique fermé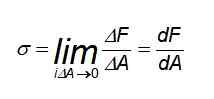

Alors en général, la valeur de l'effort à un point particulier peut être différente de la valeur moyenne. En fait, l'effort peut varier en fonction de la section pour considérer.

Ceci est illustré dans la figure suivante, dans laquelle les forces de traction F tentent de séparer la barre en équilibre dans les sections MM et nn.

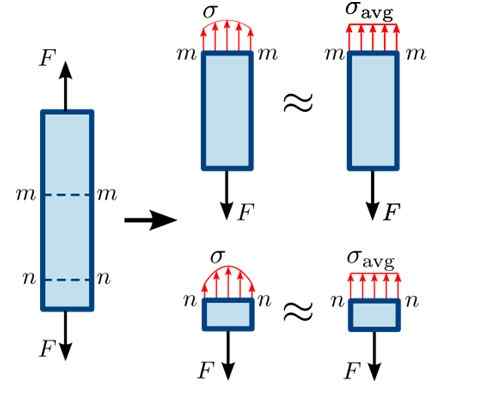figure 3. Distribution des efforts normaux dans différentes sections d'une barre. Source: https: // communes.Wikimedia.org / wiki / fichier: normal_stress.SVG # / Media / Fichier: Normal_stress.SVG

Comme la section nn Il est très proche de l'endroit où la force F en baisse, la distribution des forces à la surface n'est pas entièrement homogène, ces mineurs étant les plus loin de ce point. La distribution est un peu plus homogène dans la section MM.

Dans tous les cas, l'effort normal a toujours tendance à étirer ou à comprimer les deux parties du corps qui se trouvent des deux côtés de l'avion sur lequel ils agissent. D'un autre côté, d'autres efforts différents, comme le cisaillement, ont tendance à se déplacer et à séparer ces pièces.

La loi de Hooke et les efforts normaux

La loi de Hooke stipule que dans les limites élastiques, l'effort normal est directement proportionnel à la déformation subie par la barre ou l'objet. Dans ce cas:

Effort normal ∝ Déformation unitaire

La constante de proportionnalité étant le jeune (Y) module:

Effort normal (σ) = jeune module (y) x déformation unitaire (ε)

σ = y. ε

Avec ε = Δl / l, où Δl est la différence entre la longueur finale et la longueur initiale, qui est L.

Le jeune module ou module d'élasticité est une caractéristique du matériau, dont les dimensions sont les mêmes que celles de l'effort, car la déformation unitaire est sans dimension.

Il peut vous servir: 13 exemples de la deuxième loi de Newton dans la vie quotidienne

Importance de l'effort dans la résistance des matériaux et de la géologie

Il est très important de déterminer à quel point les matériaux aux efforts sont résistants. Pour les structures utilisées dans la construction de bâtiments, ainsi que dans la conception de pièces pour différents appareils, il est nécessaire de s'assurer que les matériaux choisis remplissent correctement leur fonction.

Par conséquent, les matériaux sont analysés de manière exhaustive dans les laboratoires par des essais destinés à savoir combien de force ils peuvent résister avant de se déformer et de se briser, perdant ainsi leurs fonctions. Sur la base de cela, la décision est prise de la fabrication ou non d'une certaine pièce ou de faire partie d'un appareil.

On pense que le premier scientifique à étudier systématiquement la résistance des matériaux était Leonardo da Vinci. Il a laissé des preuves de procès dans lesquels il a déterminé la résistance des fils suspendus aux pierres de différents pesos.

Dans les efforts à la fois l'ampleur de la force et aussi les dimensions de la structure et la façon dont elle est appliquée est importante, afin d'établir les limites dans lesquelles le matériau a un comportement élastique; c'est-à-dire qu'il revient à sa forme d'origine lorsque l'effort cesse.

Avec les résultats de ces tests, les courbes de déformation d'effort sont effectuées pour différents types de matériaux, tels que l'acier, le béton, l'aluminium et bien d'autres.

Exemples

Dans les exemples suivants, on suppose que les forces sont réparties uniformément et que le matériel est homogène et isotrope. Cela signifie que ses propriétés sont les mêmes dans n'importe quelle direction. Par conséquent, il est valable d'appliquer l'équation σ = p / a pour trouver des efforts.

-Exercice 1

Dans la figure 3, il est connu que l'effort normal moyen agissant sur la section AB a une magnitude de 48 kPa. Trouver: a) l'ampleur de la force F qui agit dans CB, b) l'effort sur la section BC.

Il peut vous servir: tir horizontal: caractéristiques, formules et équations, exercices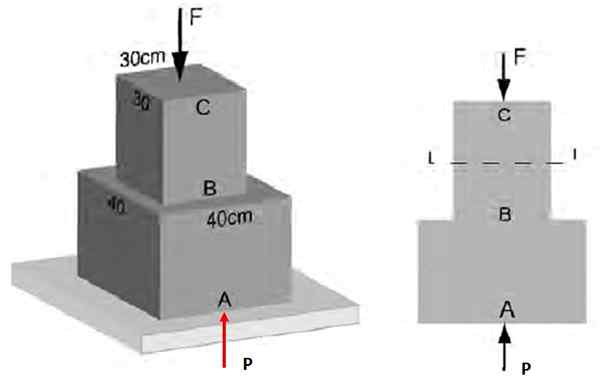Figure 4. Efforts normaux sur la structure de l'exemple 1 ..

Solution

Puisque la structure est en équilibre statique, selon la deuxième loi de Newton:

P-f = 0

L'effort normal sur la section AB a une magnitude:

σ_{UN B} = P / A_{UN B}

Où p = σ_{UN B} . POUR_{UN B} = 48000 PA. (40 x 10 ^-2 m)² = 7680 n

Donc f = 7680 n

L'effort normal sur la section BC est le rapport entre l'ampleur de F et la zone de la section transversale de ce côté:

σ_{avant JC} = F / a_{avant JC} = 7680 n / (30 x 10 ^-2 m)² = 85.3 kpa.

-Exercice 2

Un fil de 150 m de long et 2.5 mm de diamètre est étiré par une force de 500 n. Trouver:

a) effort longitudinal σ.

b) Déformation unitaire, sachant que la longueur finale est de 150.125 m.

c) le module d'élasticité ET de ce fil.

Solution

a) σ = f / a = f / π.r²

Le rayon du fil est la moitié du diamètre:

R = 1.25 mm = 1.25 x 10^-3 m.

La zone de section croisée est π.r², Ensuite, l'effort est:

σ = f / π.r² = 500 / (π.(1.25 x 10^-3)² PA = 101859.2 pa

b) ε = ΔL / l = (longueur finale - longueur initiale) / longueur initiale

Donc:

ε = (150.125 - 150) / 150 = 0.125/150 = 0.000833

c) Le module de fil du jeune est éliminé en connaissant les valeurs de ε et σ précédemment calculées:

Y = σ / ε = 101859.2 pa / 0.000833 = 1.22 x 10⁸ PA = 122 MPa.

Les références

1. Bière, f. 2010. Mécanique des matériaux. 5e. Édition. McGraw Hill. 7 - 9.
2. Giancoli, D.  2006. Physique: principes avec applications. 6^te  Élégant. Prentice Hall. 238-242.
3. Hibbeler, R.C. 2006. Mécanique des matériaux. 6e. Édition. Pearson Education. 22 -25
4. Valera Negrete, J. 2005. Notes de physique générale. Unam. 87-98.
5. Wikipédia. Stress (mécanique). Récupéré de: Wikipedia.org.