Erreur d'estimation standard comment calculé, exemples, exercices

Il Erreur d'estimation standard Mesurez l'écart dans une valeur de population d'échantillon. C'est-à-dire que l'erreur d'estimation standard mesure les variations possibles de la moyenne de l'échantillon par rapport à la valeur réelle de la moyenne de la population.

Par exemple, si vous voulez connaître l'âge moyen de la population d'un pays (moyenne de la population), un petit groupe d'habitants est pris, ce que nous appellerons des "spectacles". De là, l'âge moyen (moyenne de l'échantillon) est extrait et il est supposé que la population a cet âge moyen avec une erreur d'estimation standard qui varie plus ou moins.

M. W. Toews [cc par 2.5 (https: // CreativeCommons.Org / licences / par / 2.5)]

Il convient de noter qu'il est important de ne pas confondre l'écart type avec l'erreur standard et l'erreur d'estimation standard:

1- L'écart type est une mesure de la dispersion des données; c'est-à-dire que c'est une mesure de la variabilité de la population.

2- L'erreur standard est une mesure de la variabilité de l'échantillon, calculée en fonction de l'écart type de la population.

3- L'erreur d'estimation standard est une mesure de l'erreur qui est faite lors de la prise de la moyenne de l'échantillon comme estimation de la moyenne de la population.

[TOC]

Comment est-il calculé?

L'erreur d'estimation standard peut être calculée pour toutes les mesures obtenues dans les échantillons (par exemple, l'erreur d'estimation moyenne standard ou l'erreur standard de l'estimation de l'écart type) et mesure l'erreur qui est commise lors de l'estimation de la véritable mesure de la population à partir de sa valeur d'échantillon

À partir de l'erreur d'estimation standard, l'intervalle de confiance de la mesure correspondante est construit.

Peut vous servir: Matrice inversée: calcul et exercice résolus

La structure générale d'une formule pour l'erreur d'estimation standard est la suivante:

Erreur d'estimation standard = ± coefficient de confiance * Erreur standard

Coefficient de confiance = valeur limite d'un échantillon de statistique ou de distribution d'échantillonnage (normal ou Gauss Bell, étudiant t, entre autres) pour un certain intervalle de probabilités.

Erreur standard = écart-type de la population divisée par la racine carrée de la taille de l'échantillon.

Le coefficient de confiance indique la quantité d'erreurs standard qui sont disposées à ajouter et à soustraire adaptée à un certain niveau de confiance dans les résultats.

Exemples de calcul

Supposons que vous essayez d'estimer la proportion de personnes dans la population qui ont un comportement A, et vous voulez avoir une confiance à 95% dans leurs résultats.

Un échantillon de n personnes est prélevé et la proportion d'échantillon p et son complément Q sont déterminées.

Erreur d'estimation standard (EEE) = ± coefficient de confiance * Erreur standard

Coefficient de confiance = z = 1.96.

Erreur standard = la racine carrée de la raison entre le produit de la proportion de l'échantillon pour son complément et la taille de l'échantillon n.

À partir de l'erreur d'estimation standard, l'intervalle dans lequel la proportion de population ou la proportion d'échantillon d'autres échantillons qui peuvent être formées à partir de cette population sont établies, avec un niveau de confiance à 95%:

P -eee ≤ proportion de population ≤ p + eee

Exercices résolus

Exercice 1

1- Supposons que vous essayez d'estimer la proportion de personnes dans la population qui ont la préférence pour une formule laitière enrichie, et vous voulez avoir une confiance de 95% dans leurs résultats.

Peut vous servir: division synthétique

Un échantillon de 800 personnes est prélevé et il est déterminé que 560 personnes dans l'échantillon ont la préférence pour la formule laitière enrichie. Déterminer un intervalle dans lequel la proportion de population peut être attendue et la proportion d'autres échantillons qui peuvent être prélevés dans la population, avec une confiance de 95%

A) Calcularons la proportion d'échantillon P et son complément:

P = 560/800 = 0.70

Q = 1 -p = 1 -0.70 = 0.30

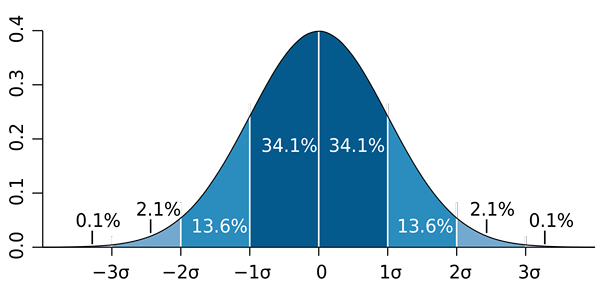
b) Il est connu que la proportion approche une distribution normale à des échantillons de grande taille (supérieurs à 30). Ensuite, la règle 68 - 95 - 99 de SO est appliquée.7 Et vous devez:

Coefficient de confiance = z = 1.96

Erreur standard = √ (p * q / n)

Erreur d'estimation standard (EEE) = ± (1.96) * √ (0.70) * (0.30) / 800) = ± 0.0318

c) À partir de l'erreur d'estimation standard, l'intervalle dans lequel la proportion de population est attendue avec un niveau de confiance à 95% est établie:

0.70 -0.0318 ≤ proportion de population ≤ 0.70 + 0.0318

0.6682 ≤ proportion de population ≤ 0.7318

Vous pouvez vous attendre à ce que la proportion d'échantillon de 70% change jusqu'à 3.18 points de pourcentage s'il prend un échantillon différent de 800 individus ou que la proportion réelle de la population se situe entre 70 et 3.18 = 66.82% et 70 + 3.18 = 73.18%.

Exercice 2

2- Nous allons prendre de Spiegel et Stephens, 2008, l'étude de cas suivante:

Sur le total des notes de mathématiques des étudiants des premiers an. Quelles sont les limites de confiance à 95% pour l'estimation de la moyenne des qualifications de mathématiques de l'université?

Il peut vous servir: quelle est la relation entre la zone du losange et le rectangle?

a) Calcularons l'erreur d'estimation standard:

Coefficient de confiance à 95% = z = 1.96

Erreur standard = s / √n

Erreur d'estimation standard (EEE) = ± (1.96) * (10√50) = ± 2.7718

b) À partir de l'erreur d'estimation standard, l'intervalle dans lequel la moyenne de la population ou la moyenne d'un autre échantillon 50 est établie, avec un niveau de confiance à 95%:

50 -2.7718 ≤ Population moyenne ≤ 50 + 2.7718

47.2282 ≤ moyenne de population ≤ 52.7718

c) Vous pouvez vous attendre à ce que la moyenne de l'échantillon change jusqu'à 2.7718 points si un échantillon différent de 50 grades est prélevé ou que la moyenne réelle des notes mathématiques de la population de l'université se situe entre 47.2282 points et 52.7718 points.

Les références

1. Abraira, V. (2002). Écart type et erreur standard. Magazine Semerne. Web récupéré.Archive.org.
2. Rumsey, D. (2007). Statistiques intermédiaires pour les mannequins. Wiley Publishing, Inc.
3. Salinas, H. (2010). Statistiques et probabilités. Récupéré du tapis.Uda.CL.
4. Sokal, R.; Rohlf, f. (2000). Biométrie. Les principes et la pratique des statistiques dans la recherche biologique. Troisième Ed. Blume Editions.
5. Spiegel, m.; Stephens, L. (2008). Statistiques. Quatrième Ed. McGraw-Hill / Inter-American du Mexique. POUR.
6. Wikipédia. (2019). 68-95-99.7 Règle. Récupéré de.Wikipédia.org.
7. Wikipédia. (2019). Erreur standard. Récupéré de.Wikipédia.org.