Formule d'énergie électromagnétique, équations, utilisations, exemples

La Énergie électromagnétique C'est celui qui se propage à travers des ondes électromagnétiques (EM). Exemple de cela est la lumière du soleil qui rayonne de chaleur, le courant qui est extrait de la sortie électrique et de celui que les rames X doivent produire des radiographies.

Comme les ondes sonores lorsqu'ils font vibrer le tympan, les ondes électromagnétiques sont capables de transférer de l'énergie qui peut plus tard devenir de la chaleur, des courants électriques ou des signaux divers.

Figure 1. Des antennes sont nécessaires dans les télécommunications. Les signes avec lesquels ils travaillent ont une énergie électromagnétique. Source: Pixabay.

L'énergie électromagnétique se propage à la fois dans un environnement matériel et vide, toujours sous la forme d'une onde transversale et l'utiliser n'est pas quelque chose de nouveau. La lumière du soleil est la principale source d'énergie électromagnétique et la plus ancienne connue, mais l'utilisation de l'électricité est un peu plus récente.

C'était juste en 1891 quand Edison Company mettre en service la première installation électrique à la Maison Blanche à Washington DC. Et cela en complément aux lumières à base de gaz qui étaient utilisées à l'époque, car au début, il y avait suffisamment de scepticisme en termes d'utilisation.

La vérité est que même, dans les endroits les plus éloignés et les plus défavorables, l'énergie électromagnétique qui arrive sans cesse de l'espace continue de maintenir la dynamique que nous appelons notre maison dans l'univers.

[TOC]

Formule et équations

Les ondes électromagnétiques sont des ondes transversales, dans lesquelles le champ électrique ET Et le champ magnétique B Ils sont perpendiculaires les uns aux autres, étant également la direction de propagation de l'onde perpendiculaire aux champs.

Toutes les vagues sont caractérisées par leur fréquence. Il s'agit du large éventail de fréquences des ondes EM, qui leur donne la polyvalence lors de la transformation de leur énergie, qui est proportionnelle à la fréquence.

La figure 2 montre une onde électromagnétique, en elle le champ électrique ET En bleu, oscille dans l'avion zy, Le champ magnétique B En rouge, il le fait dans l'avion Xy, Tandis que la vitesse de la vague est dirigée le long de l'axe +et, Selon le système de coordonnées indiqué.

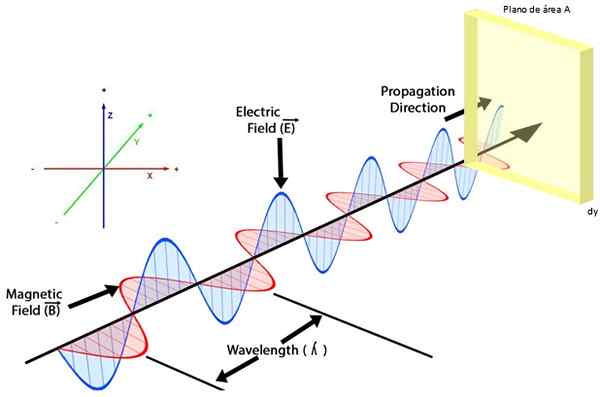Figure 2. Une onde électromagnétique affectant une surface fournit de l'énergie selon le vecteur Poynting. Source: F. Zapata.

Si sur le chemin des deux vagues, une surface est apportée, disons un plan de zone POUR et épaisseur Dy, de sorte qu'il est perpendiculaire au taux d'onde, le flux d'énergie électromagnétique par unité de surface, indiqué S, est décrit à travers Vecteur de Poynting:

S = (1 / μ_soit) ET × B

μ_soit C'est la perméabilité du vide (μ_soit = 4π .dix^-7 Tesla. Metro / ampère), Une constante liée à la facilité que le milieu donne à l'onde électromagnétique pour se déplacer.

Peut vous servir: nain blanc

Le vecteur de Poynting a été introduit par l'astrophysicien anglais John Henry Poynting en 1884, un pionnier de l'étude énergétique des champs électriques et magnétiques.

Puissance instantanée par unité de surface

Maintenant, nous devons prendre en compte que l'énergie est un scalaire, tandis que S C'est un vecteur.

Rappelant que la puissance est l'énergie livrée par unité de temps, puis le module de S Indique le Puissance instantanée par unité de surface dans le sens de la propagation de l'onde électromagnétique (taux de transfert d'énergie).

Puisque ET et B Ils sont perpendiculaires les uns aux autres, le module de ET X B C'est simplement eb Et la puissance instantanée (un scalaire) reste:

S = (1 / μ_soit) Eb

Il est facile de vérifier que les unités S sont watt / m² Dans le système international.

Il y a encore plus. Les amplitudes des champs ET et B Ils sont liés les uns aux autres à travers la vitesse de la lumière c. En fait, les ondes électromagnétiques dans le vide se propagent comme ce rapide. Cette relation est:

E = CB

Le remplacement de cette relation dans S est obtenu:

S = (1 / μ_soit.CE²

Le vecteur Poynting varie avec le temps de sinusoïdal, donc l'expression précédente est sa valeur maximale, car l'énergie délivrée par l'onde électromagnétique oscille également, tout comme les champs le font. Bien sûr, la fréquence de l'oscillation est très grande, il n'est donc pas possible de le détecter en lumière visible, par exemple.

Applications

Parmi les multiples utilisations qui, selon nous, ont déjà une énergie électromagnétique, en voici deux qui sont continuellement utilisées dans de nombreuses applications:

Antenne dipolo

Les antennes remplissent partout l'espace avec des ondes électromagnétiques. Il existe des émetteurs qui transforment les signaux électriques en ondes radio ou micro-ondes, par exemple. Et il y a des récepteurs qui font le travail inverse: ils collectent les vagues et les font des signaux électriques.

Voyons comment créer un signal électromagnétique qui se propage dans l'espace, à partir d'un dipôle électrique. Le dipôle se compose de deux charges électriques d'orgueil et de signes opposés, séparés par une petite distance.

Peut vous servir: conducteurs électriques

Dans la figure suivante, le champ électrique ET Lorsque la charge + est en place (figure de gauche). ET Points vers le bas au point montré.

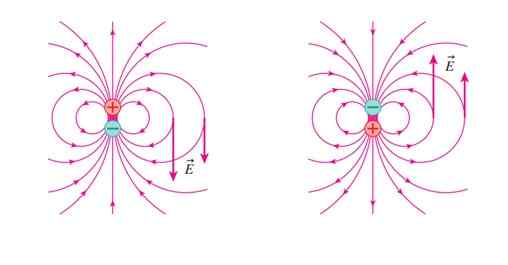figure 3. Champ électrique d'un dipôle dans deux positions différentes. Source: Randall Knight. Physique pour les scientifiques et les ingénieurs.

Dans la figure 3 à droite, la position dipolaire a changé et maintenant ET pointe. Nous répétons ce changement plusieurs fois et très rapidement, disons la fréquence F. Un champ est créé ainsi ET Variable dans le temps donne naissance à un champ magnétique B, également variable et dont la forme est sinusoïdale (voir figure 4 et en dessous de l'exemple 1).

Et comment la loi de Faraday garantit qu'un champ magnétique B Variable dans le temps donne naissance à un champ électrique, car il s'avère que la fabrication du dipôle a déjà un champ électromagnétique capable de se propager.

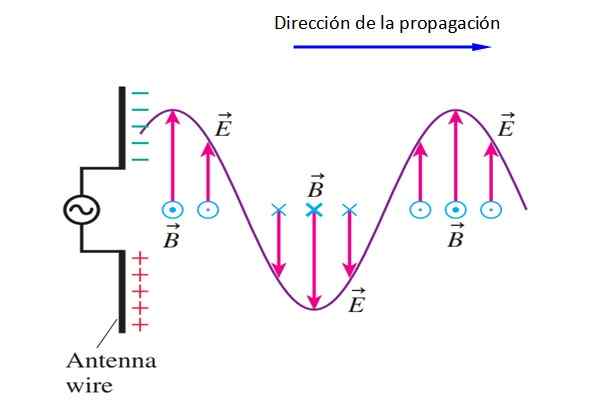Figure 4. Une antenne dipolaire génère un signal qui transporte l'énergie électromagnétique. Source: F. Zapata.

Je sens ça B points à l'intérieur ou à l'extérieur de l'écran alternativement (il est toujours perpendiculaire ET).

Énergie du champ électrique: le condenseur

Les condensateurs ont la vertu du stockage de la charge électrique et donc de l'énergie électrique. Ils font partie de nombreux appareils: moteurs, radio et circuits télévisés, système de lumière de voiture et bien plus encore.

Les condensateurs se composent de deux conducteurs séparés à une petite distance. Chacun est conféré une charge d'égalité et du signe opposé, puis créant un champ électrique dans l'espace entre les deux pilotes. La géométrie peut varier, étant bien connue de celle du condensateur de plaque parallèle plat.

L'énergie stockée dans un condenseur vient du travail qui a été fait pour le charger, qui a servi à créer le champ électrique à l'intérieur. Présentation d'un matériau diélectrique entre les plaques, la capacité du condensateur augmente et donc l'énergie que cela peut stocker.

Un condensateur de capacité et initialement déchargé, qui est chargé par une batterie qui fournit une tension V, jusqu'à atteindre une charge Q, stocke une énergie ou donnée par:

U = ½ (q²/ C) = ½ qv = ½ cv²

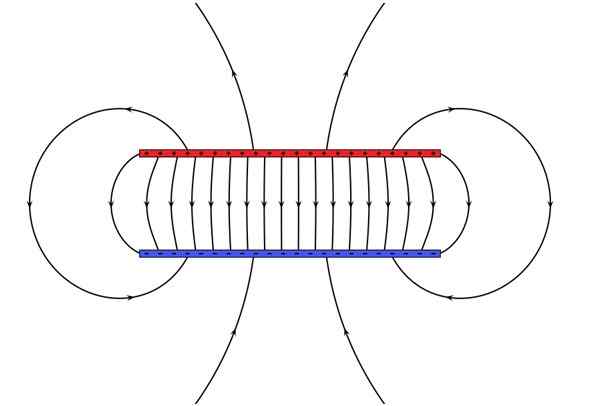Figure 5. Une plaques plates parallèles condenseur stocke l'énergie électromagnétique. Source: Wikimedia Commons. Geek3 [cc by-sa 4.0 (https: // CreativeCommons.Org / licences / by-sa / 4.0)].

Exemples

Exemple 1: Intensité d'une onde électromagnétique

Auparavant, il a été dit que l'amplitude du vecteur Poynting équivaut à la puissance que l'onde offre pour chaque mètre carré de surface, et que, en plus, étant le vecteur dépendant du temps, sa valeur oscillée jusqu'à un maximum d'un maximum de maximum de S = S = (1 / μ_soit.CE².

La valeur moyenne de S dans un cycle d'onde est facile à mesurer et à indiquer l'énergie des vagues. Cette valeur est connue sous le nom intensité des vagues Et il est calculé de cette manière:

Peut vous servir: quel est l'équilibre dynamique? (Avec exemple)

I = s_moitié = S = (1 / μ_soit.CE²_moitié

Une onde électromagnétique est représentée par une fonction sinusoïdale:

E = e_soit Sen (Kx - ωt)

Où ET_soit C'est l'amplitude de l'onde, k Le numéro d'onde et Ω La fréquence angulaire. Ensuite:

La valeur moyenne de la fonction SEN² X en un cycle est ½. Il est officiellement calculé par l'expression suivante, qui est possible à vérifier à l'aide d'une table intégrale ou à effectuer l'intégrale analytiquement:

Donc s_moitié Il reste comme:Lorsqu'une source émet également dans toutes les directions, la puissance est rayonnée en fonction de l'inverse au carré de la distance à la source (figure 5). Ouais P_m C'est la puissance moyenne, alors, à distance r L'intensité Toi du signal, il est donné par:

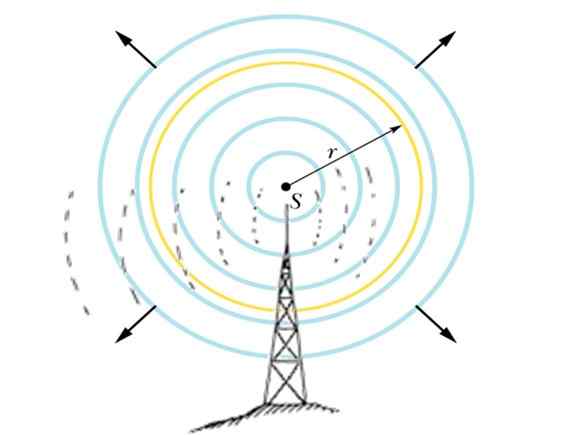Figure 5. L'antenne rayonne le signal sous forme sphérique. Source: F. Zapata.

Exemple 2: Application à une antenne d'émission

Il existe une station de radio qui transmet un signal de puissance et de fréquence de 10 kW de 100 MHz, qui se propage sous forme sphérique, comme sur la figure ci-dessus.

Trouver: a) L'amplitude des champs électriques et magnétiques à un point situé à 1 km de l'antenne et b) l'énergie électromagnétique totale qui affecte une feuille carrée de 10 cm en une période de 5 minutes.

Les données sont:

Vitesse lumineuse dans le vide: c = 300.000 km / s

Perméabilité sous vide: μ_soit = 4π .dix^-7 T.M / A (Tesla. Metro / ampère)

Solution à

L'équation donnée dans l'exemple 1 est utilisée pour trouver l'intensité de l'onde électromagnétique, mais d'abord les valeurs du système international doivent être exprimées:

10 kW = 10000 W

100 MHz = 100 x 10⁶ HZ

IR Ces valeurs sont remplacées dans l'équation de l'intensité, car c'est une source qui émet également (source isotrope):

Il s'agit précisément de la puissance moyenne par unité de surface ou de valeur moyenne du module Vector Poynting:

Auparavant, on disait que les amplitudes de ET et B Ils étaient liés par la vitesse de la lumière:

E = CB

B = (0.775/300.000.000) t = 2.58 x 10^-9 T

Solution B

S_moitié C'est la puissance par unité de surface et, à son tour, la puissance est l'énergie par unité de temps. Multiplier s_moitié Pour la zone de la plaque et pour le temps d'exposition, le résultat demandé est obtenu:

5 minutes = 300 secondes

Zone = (10/100)²  m² = 0.01 m².

U = 0.775 x 300 x 0.01 Joules = 2.325 Joules.

Les références

1. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 6. Électromagnétisme. Édité par Douglas Figueroa (USB). 307-314.
2. ICES (Comité international sur la sécurité électromagnétique). Faits d'énergie électromagnétique et vue qualitative. Récupéré de: ices-emfsafety.org.
3. Chevalier, r. 2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson. 893 - 896.
4. Université d'État de Portland. Em Waves Trate Energy. Récupéré de: pdx.Édu
5. Qu'est-ce que l'énergie électromagnétique et pourquoi est-ce important?. Récupéré de: sciencestruck.com.