Équation générale d'une ligne dont la pente est égale à 2/3

L'équation générale d'une ligne l est la suivante: AX + par + c = 0, où a, b et c sont constants, x est la variable indépendante E et la variable dépendante.

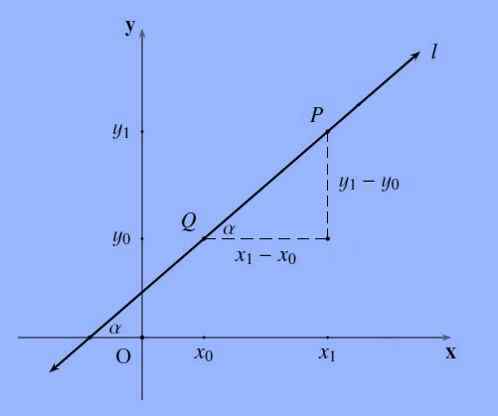
La pente d'une ligne, désignée de manière générale par la lettre m, qui passe par les points p = (x1, y1) et q = (x0, y0) est le quotient suivant m: = (y1-y0) / (x1 -X0).

La pente d'une ligne droite représente l'inclinaison; Dit plus formellement, la pente d'une ligne est la tangente de l'angle que cette forme avec l'axe x.

Il convient de noter que l'ordre dans lequel les points sont nommés est indifférent, puisque (y0-y1) / (x0-x1) = - (y1-y0) / (- (x1-x0)) = (y1-y0) / (X1-x0).

Ligne en attente

Si deux points sont connus à travers lesquels une ligne passe, il est facile de calculer sa pente. Mais que se passe-t-il si ces points ne sont pas connus?

Compte tenu de l'équation générale d'une ligne ax + by + c = 0, il doit.

Quelle est l'équation générale d'une ligne dont la pente est 2/3?

Comme la pente de la ligne est 2/3, alors l'égalité est établie -a / b = 2/3, ce qui peut voir que a = -2 et b = 3. De sorte que l'équation générale d'une ligne avec une pente égale à 2/3 est -2x + 3y + c = 0.

Il convient de préciser que si vous êtes choisi a = 2 et b = -3, la même équation sera obtenue. En effet, 2x -3y + c = 0, ce qui est égal à celui précédent multiplié par -1. Le signe de C n'a pas d'importance, car c'est une constante générale.

Une autre observation qui peut être faite est que pour a = -4 et b = 6, la même ligne est obtenue, bien que son équation générale soit différente. Dans ce cas, l'équation générale est de -4x + 6y + c = 0.

Y a-t-il d'autres moyens de trouver l'équation générale de la ligne?

La réponse est oui. Si la pente d'une ligne est connue, il existe deux formes, supplémentaires à la précédente, pour trouver l'équation générale.

Pour cela, l'équation ponctuelle et l'équation de coupe sont utilisées.

-L'équation ponctuelle: si m est la pente d'une ligne et p = (x0, y0) un point où il passe, alors l'équation y-y0 = m (x-x0) est appelée l'équation en instance de points.

-L'équation en cours de coupe: si m est la pente d'une ligne et (0, b) est la coupe de la ligne avec l'axe y, alors l'équation y = mx + b est appelée l'équation en attente de coupe.

En utilisant le premier cas, il est obtenu que l'équation ponctuelle d'une ligne dont la pente est 2/3 est donnée par l'expression y-y0 = (2/3) (x-x0).

Pour atteindre l'équation générale, tous les termes sont multipliés par 3 des deux côtés et sont regroupés, obtenant ainsi que -2x + 3y + (2 × 0-3y0) = 0 est l'équation générale de la ligne, où C = 2 × 0-3y0.

Si le deuxième cas est utilisé, il est obtenu que l'équation de coupe d'une ligne dont la pente est 2/3 est y = (2/3) x + b.

Encore une fois, multipliant 3 des deux côtés et regroupant toutes les variables, il est obtenu -2x + 3y -3b = 0. Ce dernier est l'équation générale de la ligne où C = -3B.

En fait, en regardant attentivement les deux cas, on peut voir que le deuxième cas est simplement un cas particulier du premier (lorsque x0 = 0).