Équation générale de parabole (exemples et exercices)

La Équation générale de parabole contient des termes quadratiques dans X et en et, ainsi que des termes linéaires dans les deux variables plus un terme indépendant. Le premier axe de symétrie est parallèle à l'axe vertical et celui du second est l'axe horizontal.

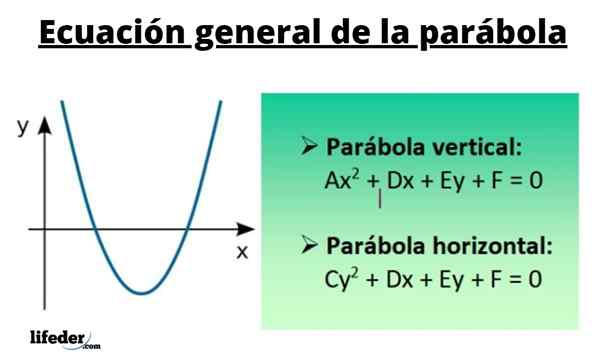
En général, l'équation quadratique qui n'a pas le terme croisé Xy Il est écrit comme:

Hache² + Cycle² +Dx + ey + f = 0

Les valeurs de A, C, D, E et F sont des nombres réels. Imposant les conditions à ∙ c = 0 et a + c ≠ 0, la courbe qui résulte de la graphique des points qui satisfont cette équation est une parabole.

Cas 1

Pour une parabole verticale, son équation générale est:

Hache² + Dx + ey + f = 0

Où a et e sont différents de 0. En d'autres termes, lorsqu'un terme apparaît avec x², La parabole est verticale.

Cas 2

Pour sa part, pour la parabole horizontale, vous avez:

Cycle² + Dx + ey + f = 0

Ici c et d sont également différents de 0, donc le terme quadratique correspond à et².

Dans tous les cas, l'équation générale de la parabole est quadratique dans l'une des variables et linéaires dans l'autre.

Éléments de parabole

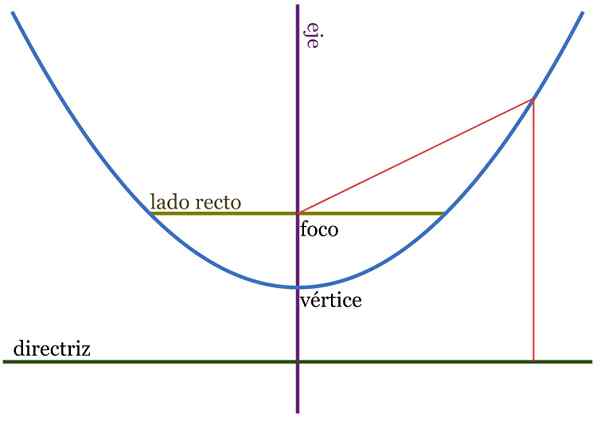Figure 2. Éléments de parabole. Les distances QF et QH sont égales. Source: Wikimedia Commons.

La parabole, définie comme un lieu géométrique, se compose de l'ensemble de points d'un avion qui équivaut à un autre point appelé se concentrer Et aussi d'une ligne, connue sous le nom directive directe.

De l'équation générale, il est possible d'étudier la parabole en spécifiant ses éléments. Y compris l'objectif et la directive, ces éléments décrits sont brièvement:

-Axe, qui fait référence à l'axe de symétrie de la parabole, peut être horizontal (parallèle à l'axe de l'abscisse) ou vertical (parallèle à l'axe des ordonnées).

Peut vous servir: facteur commun pour le regroupement des termes: exemples, exercices

-Orientation, qui à son tour correspond à l'orientation de l'axe. La parabole est verticale si son axe de symétrie est vertical, et il est horizontal lorsque l'axe est également.

-Sommet, C'est le moment où l'axe croise la parabole.

-Se concentrer, point situé sur l'axe, à l'intérieur de la parabole et à distance p du sommet. Tous les points de la parabole équidist l'objectif et la direction de la directive.

-Paramètre, C'est la distance p Entre le foyer et le sommet.

-Directive directe, qui est perpendiculaire à l'axe y et aussi à une distance p du sommet de la parabole, mais ne le coupe pas, car il est à l'extérieur.

-Côté droit, C'est la corde qui passe par la focalisation, croisant la parabole en deux points, perpendiculaire à son axe.

-Excentricité, que dans le cas de la parabole, cela vaut toujours 1.

-Représentation graphique.

Les informations pour déterminer tous ces éléments sont contenues dans l'équation générale.

La forme canonique

Pour déterminer les éléments de la parabole, il est parfois pratique de passer la forme générale à la forme canonique de la même chose, au moyen de la méthode de compléter les carrés dans la variable quadratique.

Cette forme canonique est:

(X-H)² = 4p (Y-K)

Où le point (h, k) est le sommet V de la parabole. La forme canonique de l'équation générale peut également devenir, développant le produit notable et réorganisant les termes.

Exemples

Exemple 1

Voici les équations de parabole en général:

a) 4x² + 5y - 3 = 0

b) 1 - 2y + 3x-et² = 0

En a) les coefficients sont identifiés: a = 4, c = 0, d = 0, e = 5, f = -3. C'est une parabole dont l'axe de symétrie est vertical.

Peut vous servir: division synthétique

De sa part, en b) l'équation générale demeure:

- et² + 3x - 2y + 1 = 0

Et les coefficients sont: c = -1, d = 3, e = -2 et f = 1.

Exemple 2

La parabole suivante est sous une forme canonique:

(Y-1)² = 6 (x-3)

Pour trouver son équation générale, le produit notable est développé et la parenthèse est réalisée à droite:

et² -2y + 1 = 6x -18

Maintenant, tous les termes de gauche sont passés et ils sont regroupés de manière pratique:

et² -2y + 1- 6x +18 = 0 → et² - 6x -2y + 19 = 0

Comme le terme quadratique est et² C'est une parabole horizontale. Les coefficients sont:

C = 1; D = -6; E = -2, f = 19.

Exercices résolus

Exercice 1

La parabole suivante est donnée en général:

X² -10x -12y - 11 = 0

On demande de l'écrire sous la forme canonique.

Solution

Aller au formulaire canonique est obtenu en complétant les carrés, dans ce cas, en variable x. Les termes en x commencent entre parenthèses:

(X² -10x) -12y - 11 = 0

Vous devez transformer ce qui est entre parenthèses en un trinôme carré parfait, qui est réalisé en ajoutant 5², qui doit naturellement être soustrait, car sinon l'expression est modifiée. Il reste comme ceci:

(X² −10x + 5²) −12y - 11−5²= 0

Les trois termes entre parenthèses constituent le trinôme carré parfait (X-5)². Il peut être vérifié en développant ce produit notable pour corroborer. Maintenant, la parabole reste:

(X-5)² -12y -36 = 0

Ce qui suit est de prendre en compte les termes en dehors de la parenthèse:

(X-5)² -12 (y +3) = 0

Qui se transforme enfin en:

(X-5)² = 12 (y +3)

Exemple 2

Trouvez les éléments de la parabole précédente et construisez vos graphiques.

Solution

Sommet

Le sommet de la parabole a des coordonnées V (5, -3)

Cela peut vous servir: prisme hépagonal

Axe

La ligne x = 5.

Paramètre

Concernant la valeur du paramètre p qui apparaît sous la forme canonique: (X-H)² = 4p (Y-K) compare les deux équations:

4p = 12

P = 12/4 = 3

Orientation

Cette parabole est verticale et s'ouvre. Comme le sommet est situé à x = 5, y = -3, alors l'axe de symétrie est la ligne verticale x = 5.

Se concentrer

L'accent est mis sur la ligne x = 5, il a donc une coordonnée x = 5 également.

La coordonnée et De l'accent doit être des unités P au-dessus de K, c'est-à-dire: p + k = 3 + (-3) = 0, alors le foyer est au point (5.0).

Directive directe

Il est perpendiculaire à l'axe, donc il est de la forme y = c, maintenant, comme une distance p du sommet est loin de, mais en dehors de la parabole, cela signifie qu'il est à une distance p en dessous de K:

y = k -p = -3-3 = -6

Côté droit

Ce segment passe à la parabole, passe par l'orientation et est parallèle à la directive, donc elle est contenue dans la ligne y = 0.

Représentation graphique

Il peut être facilement obtenu à partir de logiciels graphiques en ligne gratuits, tels que Geogebra. Dans la boîte d'entrée, il est placé comme suit:

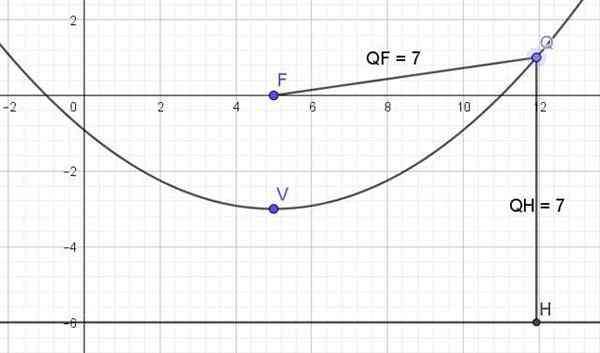figure 3. Graphique de la parabole x² -10x -12y - 11 = 0. Source: F. Zapata.

Les références

1. Baldor. 1977. Algèbre élémentaire. Éditions culturelles vénézuéliennes.
2. Hoffman, J. Sélection de problèmes de mathématiques. 2ieme volume.
3. Jiménez, R. 2008. Algèbre. Prentice Hall.
4. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
5. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.