Équation de continuité

Nous expliquons quelle est l'équation de continuité, sa formule, ses applications, ses exemples et proposer des exercices pour résoudre

Quelle est l'équation de continuité?

La équation de continuité, Pour le liquide incompressible, il établit que la masse totale d'un fluide qui circule à travers un tube, sans perte ni bénéfice, reste constante. En d'autres termes, la pâte est conservée sans changements à mesure que le fluide se déplace.

Un fluide incompressible est que dont la densité reste approximativement constante tout en coulant. Par exemple, l'eau est un liquide considéré comme incompressible dans des conditions de pression et de température standard.

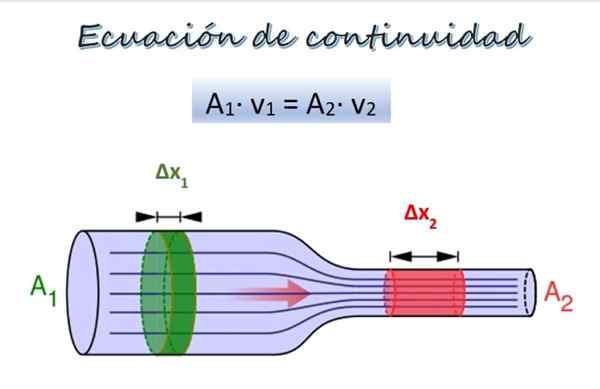
Il existe une manière mathématique d'exprimer la conservation de la masse, dans l'équation de continuité, donnée par:

POUR₁∙ V₁ = A₂∙ V₂

Où V₁ et V₂ Ils représentent la vitesse du liquide en deux sections d'un tuyau, tandis que₁ déjà₂ Ce sont les zones de section croisée respectives.

Le produit de la zone de section transversale par vitesse est appelée couler Et l'équation de continuité implique que, tout au long du tuyau, l'écoulement est constant. Le flux est également connu sous le nom débit volumique, Il est compris en observant soigneusement l'expression précédente, dont les dimensions sont le volume par unité de temps.

Formule

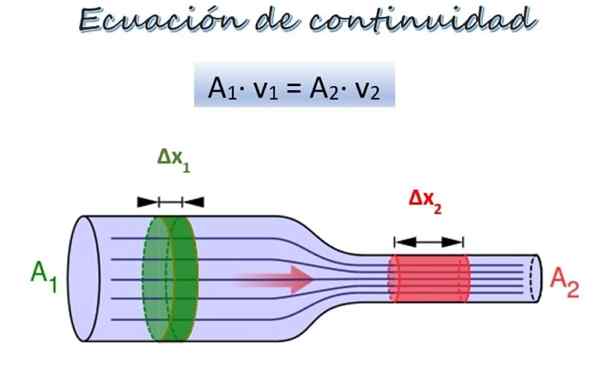L'équation de continuité pour l'écoulement d'un fluide le long d'un tuyau de différents diamètres. Source: Wikimedia Commons / F. Zapata.

Dans l'image supérieure, il y a un tuyau avec deux sections de diamètre différent et à la même hauteur, bien qu'ils puissent être à des hauteurs différentes sans représenter un problème.

Dans la section 1, plus large, la zone de section transversale est de₁ Et le fluide se déplace avec la vitesse v₁, Alors que dans la section 2, plus étroit, la zone de section croisée est de₂ et la vitesse du fluide est V₂.

Une partie de la pâte Δm₁ (vert) se déplace par la section 1 dans un temps Δt. Pendant cette période, la partie Δm₂ (rouge) voyager à travers la section 2. Comme le fluide est incompressible, sa densité est la même à tous ses points, donc à partir de la définition de la densité:

Il peut vous servir: Gase constante: ce que c'est, le calcul et les exemples

Ici ρ est densité, m est la masse et le volume V. Selon cela, la masse Δm₁ est égal à:

Δm₁ = ρ ∙ v₁

Où le volume V₁ C'est le produit entre la section transversale et la distance Δx₁:

Δm₁ = ρ ∙ (a₁ ∙ Δx₁)

Mais depuis:

Puis la partie de la pâte Δm₁ Vous pouvez écrire, en termes de vitesse et de temps Δt comme:

Δm₁ = ρ ∙ a₁ ∙ Δx₁ = ρ ∙ a₁ ∙ (V₁ ∙ Δt)

Analogue La partie Δm est écrite₂ qui circule en même temps par la section 2:

Δm₂ = ρ ∙ a₂ ∙ Δx₂ = ρ ∙ a₂ ∙ (V₂ ∙ Δt)

Par conservation de la masse:

Δm₁ = Δm₂

ET:

ρ ∙ a₁ ∙ V₁ ∙ Δt = ρ ∙ a₂ ∙ V₂ ∙ Δt

Comme ΔT et ρ sont annulés, résultats:

POUR₁ ∙ V₁ = A₂ ∙ V₂

Le flux q

Le produit de la section transversale A par la vitesse du fluide V est appelé débit et dénote Q. Il équivaut au volume de fluide par unité de temps à travers le tuyau ou à l'écoulement de volume:

 V Volume et Δt l'intervalle de temps. Le débit dans le système international des unités est m³/ s, bien que les pieds cubes, les gallons / min, les gallons / s a ​​des litres / s et gallons / s sont fréquents. Certains des facteurs de conversion les plus utilisés sont les suivants:

• 1 m³/ S = 264.172 gal / s
• 1 l / s = 0.001 m³/
• 1 pieds³/ S = 0.0283168 M³/
• 1 l / s = 0,264172 gal / s
• 1 m³/ S = 15850,3 gal / min

Notez qu'en diminuant la section transversale du tube, la vitesse du fluide augmente, et vice versa, si la section transversale augmente, alors la vitesse diminue pour que l'écoulement soit constant.

Applications et exemples

L'équation de continuité est utilisée dans l'analyse de l'écoulement du fluide, en combinaison avec l'équation de Bernoulli, dans laquelle les variations de la vitesse du fluide dans les différentes sections sont prises en compte, ainsi que les changements de pression et l'effet de la hauteur.

Peut vous servir: courant direct

Exemple 1

Dans le tuyau de jardin familial, lorsque l'eau quitte normalement le jet a une certaine plage, mais s'il met son doigt à la sortie du tuyau, réduisant le trou de sortie, la plage du jet est plus grande est.

Ici, l'équation de continuité est remplie, car, en diminuant la zone de la buse de sortie, la vitesse du jet augmente de sorte que la surface de vitesse par vitesse est constante.

Exemple 2

Le jet d'eau se rétrécit lorsqu'il tombe, car sa vitesse augmente. De cette façon, la vitesse du produit par zone reste constante

Un autre exemple où l'équation de continuité est mise en évidence est le jet d'eau qui se rétrécit lorsqu'il tombe, en raison de l'augmentation de la vitesse de l'eau pendant l'automne.

De cette façon, l'écoulement est constant, tandis que le jet continue de couler dans un régime laminaire, c'est-à-dire que l'eau tombe doucement sans turbulence ni tourbillon.

Exercices résolus

Exercice 1

L'eau circule à travers un tuyau de 20 cm de diamètre. Sachant que l'écoulement est de 2000 L / s, trouvez la vitesse de l'eau dans le tuyau.

• Solution

Il est pratique d'exprimer tout en unités du système international. Premièrement, la section transversale du tuyau est calculée, se rappelant que le rayon est la moitié du diamètre:

A = π ∙ (d / 2)²

D = 20 cm = 0.2 m

Par conséquent, la zone est:

A = π ∙ (d / 2)² = A = π ∙ (0.2 m / 2)² = 0.0314 M².

Le flux est exprimé en m³/ s à l'aide du facteur de conversion approprié:

Q = 2000 l / s = 2 m³/

À partir de la formule Q = a ∙ v La vitesse à laquelle le fluide circule à travers le tuyau est éliminé:

Exercice 2

Vous avez un tuyau de section croisée variable à travers lequel l'eau circule. À un certain point, la section transversale est 0.070 m² Et la vitesse de l'eau est 3.50 m / s. Calculer:

Peut vous servir: PASCAL PRINCIPE: HISTOIRE, applications, exemples

a) La vitesse de l'eau à un autre point du tuyau dont la zone de section transversale est 0.105 m².

b) Le volume d'eau qui est déchargé par une extrémité ouverte en 1 heure.

• Solution à

L'équation de continuité est utilisée, correspondant au flux du premier point avec le flux du second. Le flux est:

Q = A ∙ V

Pour la continuité:

Q₁ = Q₂

POUR₁ ∙ V₁ = A₂ ∙ V₂

Maintenant, ils remplacent les données fournies par l'énoncé:

• POUR₁ = 0.070 m²
• V₁ = 3.50 m / s
• POUR₂ = 0.105 m²
• V₂ =?

Et efface V₂:

Solution B

Étant donné que le flux est également le volume par unité de temps, il doit:

Par conséquent, le volume V est:

V = q ∙ Δt = (a ∙ v) Δt

Le flux qui peut être calculé avec les données du point 1 ou de celles du point 2, car elle est la même aux deux points:

Q = A₁ ∙ V₁ = 0.070 m² ∙ 3.50 m / s = 0.245 m³ /

Sachant que 1 heure = 3600 s, le volume d'eau déchargé est:

V = q ∙ Δt = (0.245 m³ / s) × (3600 s) = 882 m³

En 1 heure 882 m sont téléchargés³ d'eau à travers le tuyau.