Formules de distribution hypergéométrique, équations, modèle

La distribution hypergéométrique Il s'agit d'une fonction statistique discrète, adéquate pour calculer la probabilité dans des expériences aléatoires avec deux résultats possibles. La condition requise pour l'appliquer est qu'il s'agit de petites populations, dans lesquelles les extractions ne sont pas remplacées et les probabilités ne sont pas constantes. 

Par conséquent, lorsqu'un élément de la population est choisi pour connaître le résultat (vrai ou faux) d'une certaine caractéristique, ce même élément ne peut pas être choisi à nouveau.

Figure 1. Dans une population de vis comme celle-ci, il y a sûrement des spécimens défectueux. Source: Pixabay.

Certes, l'élément suivant choisi est donc plus susceptible d'obtenir un vrai résultat, si l'élément précédent avait un résultat négatif. Cela signifie que la probabilité varie, dans la mesure où les éléments de l'échantillon sont extraits.

Les principales applications de la distribution hypergéométrique sont: le contrôle de la qualité dans les processus avec peu de population et le calcul des probabilités dans les jeux aléatoires.

Quant à la fonction mathématique qui définit la distribution hypergéométrique, il s'agit de trois paramètres, qui sont:

- Nombre d'éléments de population (n)

- Taille de l'échantillon (M) 

- Nombre d'événements dans la population complète avec un résultat favorable (ou défavorable) de la caractéristique étudiée (n).

[TOC]

Formules et équations

La formule de distribution hypergéométrique donne une probabilité P de quoi X Des cas favorables d'une certaine caractéristique se produisent. La façon de l'écrire mathématiquement, selon les nombres combinatoires, est:

Dans l'expression précédente N, n et m Ce sont des paramètres et X la variable elle-même. 

-La population totale est N.

-Le nombre de résultats positifs d'une certaine caractéristique binaire par rapport à la population totale est n.

-Le nombre d'éléments de l'échantillon est m.

Dans ce cas, X C'est une variable aléatoire qui prend de la valeur X et P (x) indique la probabilité d'occurrence de X cas favorables de la caractéristique étudiée.

Variables statistiques importantes

Les autres variables statistiques pour la distribution hypergéométrique sont:

- Moitié μ = m * n / n

- Variance σ ^ 2 = m * (n / n) * (1 n / n) * (n-m) / (n-1)

- Déviation typique σ qui est la racine carrée de la variance.

Modèle et propriétés 

Pour accéder au modèle de distribution hypergéométrique, il est basé sur la probabilité d'obtenir X cas favorables dans un échantillon de taille m. Cet échantillon contient des éléments qui répondent à la propriété à l'étude et aux éléments qui ne.

Rappelons-nous que n représente le nombre de cas favorables dans la population totale de N articles. Ensuite, la probabilité serait calculée comme ceci:

Peut vous servir: espace vectoriel: base et dimension, axiomes, propriétés

P (x) = (# des façons d'obtenir X # de manière défaillante) / (# Total Woards of Sélection)

Exprimant ce qui précède sous la forme de nombres combinatoires, le modèle de distribution des probabilités suivant est atteint:

Propriétés principales de la distribution hypergéométrique

Sont les suivants:

- L'échantillon doit toujours être petit, bien que la population soit importante.

- Les éléments de l'échantillon sont extraits de un, sans les incorporer à nouveau dans la population.

- La propriété à étudier est binaire, c'est-à-dire qu'elle ne peut prendre que deux valeurs: 1 soit 0, ou bien VRAI soit faux.

Dans chaque étape d'extraction d'étape, la probabilité change en fonction des résultats précédents.

Approche par distribution binomiale

Une autre propriété de distribution hypergéométrique est qu'elle peut être approchée par la distribution binomiale, désignée comme Bi, Tant que la population N être grand et au moins 10 fois supérieur à l'échantillon m. Dans ce cas, ce serait comme ceci:

P (n, n, m; x) = bi (m, n / n, x)           

Tant que n est grand et n> 10m

Exemples

Exemple 1

Supposons qu'une machine qui produit des vis et des données accumulées indiquent que 1% sortent avec des défauts. Ensuite, dans une boîte de n = 500 vis, le nombre de défauts sera:

N = 500 * 1/100 = 5

Probabilités par distribution hypergéométrique

Supposons que de cette boîte (c'est-à-dire de cette population), nous prenons un échantillon de m = 60 vis.

La probabilité qu'aucune vis (x = 0) de l'échantillon ne laisse défectueuse est de 52,63%. Ce résultat est atteint lors de l'utilisation de la fonction de distribution hypergéométrique:

P (500, 5, 60; 0) = 0,5263

La probabilité que x = 3 des vis d'échantillon laisse défectueuse est: p (500, 5, 60; 3) = 0,0129.

En revanche, la probabilité que x = 4 vis des années 60 de l'échantillon laisse défectueuse est: p (500, 5, 60; 4) = 0,0008.

Enfin, la probabilité que x = 5 vis dans cet échantillon sortent avec un défaut est: P (500, 5, 60; 5) = 0.

Mais si vous voulez connaître la probabilité que dans cet échantillon, il y a plus de 3 vis défectueuses, alors la probabilité accumulée doit être obtenue, ajoutant:

P (3) + P (4) + P (5) = 0,0129 + 0,0008 + 0 = 0,0137.

Cet exemple est illustré à la figure 2, obtenu par l'utilisation de Géogebra Logiciel gratuit à usage large dans les écoles, les instituts et les universités.

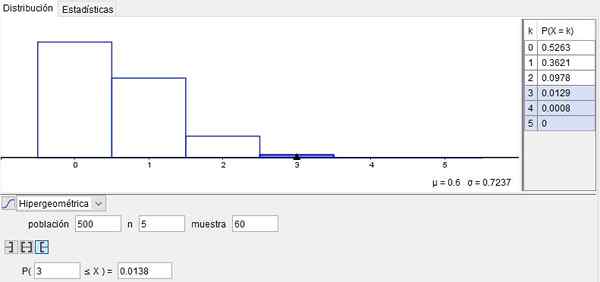Figure 2. Exemple de distribution hypergéométrique. Préparé par f. Zapata avec Geogebra.

Exemple 2

Un jeu de deck espagnol a 40 cartes, dont 10 ont de l'or et les 30 autres ne l'ont pas. Supposons que 7 cartes soient extraites de ce deck, qui ne reviennent pas au jeu.

Peut vous servir: Symétrie centrale: propriétés, exemples et exercices

Si x est le nombre d'or présents dans les 7 cartes extraites, alors la probabilité qui est X OROS dans une extraction de 7 cartes est donnée par la distribution hypergéométrique P (40,10,7; x).

Examinons ceci: Pour calculer la probabilité d'avoir 4 médailles d'or dans une extraction de 7 cartes, nous utilisons la formule de distribution hypergéométrique avec les valeurs suivantes:

Et le résultat est: 4,57% de probabilité.

Mais si vous voulez connaître la probabilité d'obtenir plus de 4 cartes, nous devrons ajouter:

P (4) + p (5) + p (6) + p (7) = 5,20%

Exercices résolus

L'ensemble d'exercices suivants est destiné à illustrer et à assimiler les concepts qui ont été présentés dans cet article. Il est important que le lecteur essaie de les résoudre seuls, avant de regarder la solution.

Exercice 1

Une usine prophylactique a révélé que sur 1000 préservatifs produits par une certaine machine, 5 sont défectueux. Pour effectuer un contrôle de la qualité, 100 préservatifs sont pris au hasard et le lot est rejeté s'il y a au moins un ou plusieurs défectueux. Répondre:

a) Quelle possibilité doit être un lot jeté?

b) Ce critère de contrôle de la qualité est-il efficace?

Solution

Dans ce cas, de très grands nombres combinatoires apparaîtront. Le calcul est difficile, sauf si un package d'ordinateur adéquat est disponible.

Mais parce qu'il s'agit d'une grande population et que l'échantillon est dix fois inférieur à la population totale, vous pouvez utiliser l'approche de la distribution hypergéométrique due à la distribution binomiale:

P (1000,5,100; x) = bi (100, 5/1000, x) = bi (100, 0.005, x) = c (100, x) * 0.005 ^ x (1-0.005) ^ (100-x)

Dans l'expression précédente C (100, x) C'est un numéro combinatoire. Ensuite, la probabilité de Haya plus d'un défectueuse sera calculée comme suit:

P (x> = 1) = 1 - bi (0) = 1-.6058 = 0.3942

C'est une excellente approche, par rapport à la valeur obtenue lors de l'application de la distribution hypergéométrique: 0.4102

On peut dire que, une probabilité de 40%, beaucoup de 100 prophylactiques devraient être rejetées, ce qui n'est pas très efficace.

Mais, être un peu moins exigeant dans le processus de contrôle de la qualité et éliminer.

Exercice 2

Une machine à taco en plastique fonctionne de telle manière que sur 10 pièces, une est déformée. Dans un échantillon de 5 pièces, cette possibilité doit être une pièce défectueuse.

Solution

Population: n = 10

Peut vous servir: Identité pythagorienne: démonstration, exemple, exercices

Numéro n défectueux pour chaque n: n = 1

Taille de l'échantillon: m = 5

P (10, 1, 5; 1) = c (1,1) * c (9,4) / c (10,5) = 1 * 126/252 = 0.5

Par conséquent, il y a une probabilité de 50% que dans un échantillon de 5, un taco sort déformé.

Exercice 3

Lors d'une réunion de jeunes lycées, il y a 7 femmes et 6 messieurs. Parmi les filles, 4 étudient les sciences humaines et 3 sciences. Dans le groupe de garçons, 1 étudie les sciences humaines et 5 sciences. Calculez ce qui suit:

a) Choisir au hasard trois filles: quelle est la probabilité d'étudier toutes les sciences humaines?.

b) Si trois participants sont choisis au hasard pour la rencontre d'amis: quels sont trois d'entre eux, quel que soit le sexe, étudiez les trois ou les sciences humaines aussi toutes les trois?.

c) Maintenant, sélectionnez deux amis au hasard et appelez X à la variable aléatoire "Nombre de ceux qui étudient les sciences humaines". Parmi les deux choisis, déterminer la valeur moyenne ou attendue de X et la variance σ ^ 2.

Solution à 

La population est le nombre total de filles: n = 7. Ceux qui étudient les sciences humaines sont n = 4, du total. L'échantillon aléatoire de filles sera m = 3.

Dans ce cas, la probabilité que les trois soient des sciences humaines soient données par la fonction hypergéométrique:

P (n = 7, n = 4, m = 3, x = 3) = c (4, 3) c (3, 0) / c (7, 3) = 0.1143

Ensuite, il y en a 11.4% de probabilité que trois chicas aléatoires étudient les sciences humaines.

Solution B

Les valeurs à utiliser sont:

-Population: n = 14

-Quantité qui étudie les lettres est: n = 6 et le

-Taille de l'échantillon: m = 3.

-Nombre d'amis qui étudient les sciences humaines: x

Selon cela, x = 3 signifie que les trois en sciences humaines d'étude, mais x = 0 signifie qu'aucune n'étudie les sciences humaines. La probabilité que les trois étudient la même est donnée par la somme:

P (14, 6, 3, x = 0) + p (14, 6, 3, x = 3) = 0.0560 + 0.1539 = 0.2099

Ensuite, nous avons une probabilité de 21% que trois participants à la réunion, choisis au hasard, étudient le même.

Solution C

Ici, nous avons les valeurs suivantes:

N = 14 population totale d'amis, n = 6 nombre total dans la population qui étudie les sciences humaines, la taille de l'échantillon est M = 2.

L'espoir est:

E (x) = m * (n / n) = 2 * (6/14) = 0.8572

Et la variance:

σ (x) ^ 2 =  m * (n / n) * (1 n / n) * (n-m) / (n-1) = 2 * (6/14) * (1-6 / 14) * (14-2) / (14 -1) =

= 2 * (6/14) * (1-6 / 14) * (14-2) / (14-1) = 2 * (3/7) * (1-3 / 7) * (12) (13)  = 0.4521

Les références

1. Distributions de probabilité discrètes. Récupéré de: biploot.usal.est
2. Statistique et probabilité. Distribution hypergéométrique. Récupéré de: projectoScartes.org
3. Cdpye-ugr. Distribution hypergéométrique. Récupéré de: ugr.est
4. Géogebra. Geogebra classique, calcul de probabilité. Récupéré de Geogebra.org
5. Homologation facile. Exercices de distribution hypergéométrique résolus. Récupéré de: probafacil.com
6. Minitab. Distribution hypergéométrique. Récupéré de: Support.Minitab.com
7. Université de Vigo. Principales distributions discrètes. Récupéré de: anapg.sites Internet.Uvigo.est
8. Vitutor. Statistiques et combinatoires. Récupéré de: Vitutor.filet
9. Weisstein, Eric W. Distribution hypergéométrique. Récupéré de: Mathworld.Wolfram.com
10. Wikipédia. Distribution hypergéométrique. Récupéré de: est.Wikipédia.com