Culture et société générales

Distribution exponentielle

3587
73
Eva Henry

Nous expliquons ce qu'est la distribution exponentielle, ses caractéristiques, ses formules, ses exemples et avons mis des exercices résolus

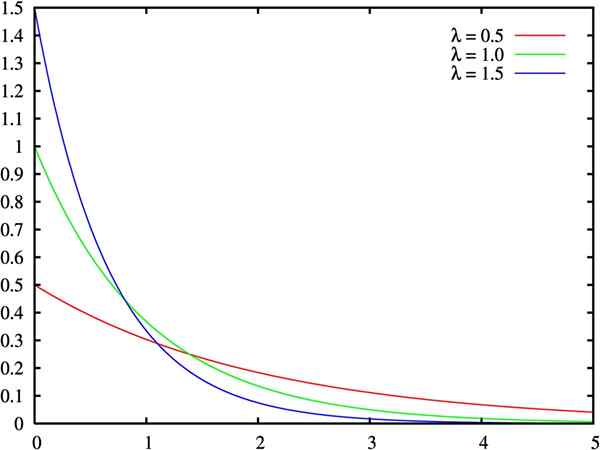
Graphique de la fonction de densité de la distribution exponentielle, pour trois valeurs du paramètre lambda. Source: Wikimedia Commons.

Qu'est-ce que la distribution exponentielle?

La distribution exponentielle C'est un modèle probabiliste pour les variables aléatoires continues. Cela signifie que, à travers lui, vous pouvez connaître la probabilité de survenue d'une certaine valeur de la variable, c'est donc une distribution de probabilité.

Pour obtenir la distribution, il commence à partir d'un fonction de densité, qui a une forme exponentielle de paramètre λ> 0:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ texte Ouais x \ leq 0 \ End cas$

La fonction de densité en tant que telle ne permet pas de calculer la probabilité, mais une fois établi F (x), la fonction de distribution F (x), par laquelle les probabilités sont obtenues, est obtenue par intégration de f (x). Par exemple, la probabilité P que la variable aléatoire prend des valeurs entre 0 et x est:

$F(x)=P[x\leq x]=\int_0^xf(x)dx$

Effectuer l'intégration, ce qui est très simple, car l'intégrale d'une exponentielle est la même exponentielle, à l'exception des constantes qui accompagnent l'argument, il est obtenu:

$F(x)=\int_0^x\lambda e^-\lambda xdx=\lambda \left (-\frac1\lambda \right )\left [ e^-\lambda x \right ]_0^x=-\left (e^-\lambda x-e^0 \right )=1-e^-\lambda x$

La distribution exponentielle est largement utilisée pour déterminer la probabilité d'un événement après un certain temps d'attente, comme le temps qui se déroule dans l'émergence d'un hôpital avant l'arrivée d'un patient.

Souvent, les événements se réfèrent à la défaillance ou à la répartition des types électriques, électroniques et autres. Dans ce cas, la distribution exponentielle aide à estimer le temps nécessaire à un composant pour échouer, ainsi que le temps entre les réparations. Ceci est connu sous le nom de théorie de la fiabilité.

Caractéristiques de la distribution exponentielle

Certaines des caractéristiques les plus remarquables de la fonction de densité f (x) de la distribution exponentielle sont les suivantes:

f (x) est positif.
La zone sous la courbe y = f (x) = λe^−λ^X Il est toujours égal à 1, car la somme des probabilités d'occurrence de toutes les valeurs de la variable doit être 1. C'est une condition que les fonctions de densité remplissent. Cette zone est calculée par l'intégrale:

Peut vous servir: Anuma

$\int_-\infty ^\infty f(x)dx=\int_-\infty ^\infty \lambda e^-\lambda xdx=1$

Manque de mémoire de distribution exponentielle

La caractéristique la plus remarquable de la distribution exponentielle est son manque de mémoire. Par exemple, supposons que le temps écoulé se moque avec cette distribution jusqu'à ce que la défaillance d'un élément se produise.

Eh bien, le manque de mémoire fait référence à savoir que l'élément a fonctionné pour un temps de survie «S», ne modifie pas la probabilité que l'élément continue de courir jusqu'à un certain temps supplémentaire «t».

C'est-à-dire que la probabilité que l'élément échoue d'ici à une certaine heure (1 minute, 1 heure, par exemple) ne dépend pas du fait d'avoir bien fonctionné jusqu'à présent.

Mathématiquement, il est calculé par définition de la probabilité d'événements indépendants:

$P[x\geq s+t/x\geq s]=\fracP[x\geq s+t]P[x\geq s]=\frac1-F(s+t)1-F(s)=\frac1- [1-e^-\lambda (s+t) ]1- [1-e^-\lambda s ]= \beginmatrix \\ \endmatrix$

$=e^-\lambda t$

Par conséquent, la probabilité ne dépend pas du s ou du temps de survie.

Formules

1.- La fonction de densité de la distribution exponentielle est:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ texte Ouais x \ leq 0 \ End cas$

Où λ est le paramètre de distribution.

2.- Comme décrit ci-dessus, la distribution des probabilités elle-même est désignée comme F (x) et les différentes probabilités sont obtenues par intégration de la fonction de densité:

$F(x)=\begincases 0 & \text si x\leq 0 \\ 1-e^-\lambda x& \text si x>0 \ End cas$

3.- À partir de ce qui précède, il s'ensuit que la probabilité que la variable prenne des valeurs inférieures ou égales à «x» est p [x≤x] = 1 −e^−λ^X.

4.- La zone sous la courbe y = f (x), incluse entre A et B, permet de calculer la probabilité que la variable soit dans l'intervalle [a, b]. Cette zone est:

P [a ≤ x ≤ b] = f (b) - f (a)

5.- La valeur de p [x ≥ a] est 1 - f (a) = 1 - (1 - e^−λ^X) = e^−λ^X

Valeur attendue de la distribution exponentielle

L'espoir ou la valeur attendue e (x) de la distribution exponentielle est la valeur qui devrait se produire plus fréquemment. Il est calculé à partir de l'intégrale:

Peut vous servir: techniques d'enregistrement d'informations

$E(x)=\int_0^\infty xf(x)dx$ Qui est facilement résolu par la méthode d'intégration par parties. Le résultat est:

E (x) = 1 / λ

Variance de la distribution exponentielle

Pour le calcul de la variance, l'intégrale doit être déterminée:

$Var(x)=\int_0^\infty x^2f(x)dx$

Qui est également résolu avec la méthode d'intégration par parties, pour obtenir:

Var (x) = 1 / λ²

Une particularité de la distribution exponentielle est que l'écart type S (x), défini comme la racine carrée de la variance est:

S (x) = √var (x) = √ (1 / λ²) = 1 / λ

C'est-à-dire que l'écart type est égal à l'espoir de distribution.

Exemples de distribution exponentielle

Datation des échantillons de carbone 14

La distribution exponentielle est utilisée pour déterminer le temps nécessaire pour désintégrer une particule radioactive. Ces heures sont utilisées pour dater les échantillons de fossiles par radiocarbone.

Le temps qu'il faut pour vérifier le courrier

Vous pouvez modéliser le temps que les utilisateurs prennent pour examiner leur e-mail, une fois la notification reçue, via une distribution exponentielle. Supposons que le paramètre de distribution soit λ = 0.2, alors, la probabilité qu'une personne prenne moins d'une minute pour revoir son e-mail est:

$P[x\leq 1]=\int_0^1f(x)dx=\int_0^10.2e^-0.2xdx$

Cette intégrale a été résolue au début, il ne reste que pour remplacer les valeurs numériques dans la solution et calculer le résultat final:

P [x ≤ 1] = 1 --e^-^0.2^×¹ = 1− e^-^0.2 = 1− 0.819 = 0.181

Il peut également être directement remplacé sur la fonction f (x) donnée ci-dessus, pour obtenir F (1).

Exercices

Exercice 1

Trouvez la probabilité qu'une personne plus tard une heure examine son e-mail, si la distribution de probabilité est exponentielle, avec paramètre λ = 0.2.

Solution

P [x ≥ 60] doit être calculé, car 1 heure équivaut à 60 minutes et la probabilité que la personne en fin de 60 minutes ou plus pour vérifier le courrier soit demandée. La probabilité est calculée avec la même intégrale présentée au début, en modifiant simplement les limites d'intégration:

Peut vous servir: Rapa Nui: histoire, caractéristiques, culture, traditions

$P[x\geq 60]=\int_60^\infty 0.2e^-0.2xdx=-\left ( -e^-0.2\times 60 \right )=0.000006144$

La valeur obtenue est petite, il est donc très peu probable qu'une personne prenne plus d'une heure pour revoir son e-mail.

Exercice 2

Les ampoules électriques ont généralement une durée finie, à l'exception de la célèbre ampoule de la caserne des pompiers de Livermore, en Californie, qui n'a jamais échoué depuis qu'elle était en cours, en 1901.

Supposons que la durée d'une ampoule actuelle suit une distribution exponentielle, avec une valeur attendue de 8 mois. Calculer:

a) Quelle est la probabilité que l'ampoule dure entre 5 et 14 mois?

b) La probabilité que l'ampoule dure plus de 25 mois, sachant qu'elle a plus de 11 mois de fonctionnement.

Solution à

La première chose est de trouver la valeur de λ, à travers la valeur attendue de la distribution e (x) = 8 mois. Selon ce qui a été dit dans la section précédente, la valeur attendue est donc l'inverse du paramètre λ:

E (x) = 1 / λ → λ = 1 / e (x) = 1/8 = 0.125

Ensuite, la probabilité demandée est calculée, au moyen de l'intégrale donnée au début, mais modifiant facilement les limites d'intégration:

Ensuite, il est remplacé dans la fonction f (x) donnée dans la section précédente, comme suit:

P [5 ≤ x ≤ 14] = f (14) - f (5) = [1 - e^{-(0.125 × 14)}] - [1 - e^{-(0.125 × 5)}] = 0.36

Solution B

Pour répondre à cette question, la propriété du manque de mémoire sera utilisée, énoncée ci-dessus. Comme on sait qu'il a déjà duré plus de 11 mois, alors:

S = 11 mois

Le délai supplémentaire pour durer 25 mois ou plus est:

T = 14 mois

P [x ≥ s + t│t ≥ s] = p [x ≥ 11 + 14│t ≥ 11] = e^{−0.125 × 14}= 0.174