Dérivés implicites comment ils sont résolus et résolus exercices

Le dérivés implicites Ce sont des outils utilisés dans une technique de différenciation appliquée aux fonctions. Ils s'appliquent lorsqu'il n'est pas possible, sous des méthodes régulières, à effectuer la clairance de la variable dépendante qui est de dériver. Cette autorisation est effectuée sur la base de la variable indépendante.

Par exemple, dans l'expression 3xy³ - 2y + xy² = xy, vous ne pouvez pas obtenir l'expression qui définit "y" en fonction de "x". De sorte que lorsque l'expression différentielle Dy / dx peut être obtenue.

[TOC]

Comment les dérivés implicites sont-ils résolus?

Pour résoudre une implication, elle est basée sur une expression implicite. Par exemple: 3xy³ - 2y + xy² - Xy = 0. Cela a déjà été clairement effacé, cependant, pour le faire, ce n'est pas une condition nécessaire pour obtenir le dérivé de y concernant x. Ensuite, chacun des éléments est dérivé de la règle de la chaîne pour les fonctions mixtes:

3xy³ Il se compose de 2 variables, donc D (3xy³) Il sera traité comme la dérivée d'un produit des fonctions.

D (3xy³) / dx = 3y³ + 3Y².(3x) et '= 3y³ + 9xy² et'

Où l'élément et 'est connu sous le nom de "et cousin»Et dy / dx représente

-2y dérive selon la loi k.U = k.OU'

D (-2y) = -2 et '

Xy² suppose un autre différentiel composé d'un produit de fonctions

D (xy²) = y² + 2xy et '

-Xy est une manière homologue

d (-xy) = -y -x et '

Ils sont remplacés en égalité, sachant que zéro dérivé est nul.

3Y³ + 9xy² et '- 2 et' + et² + 2xy et '- y - x et' = 0

Les éléments qui ont le terme et «sont regroupés d'un côté de l'égalité

Peut vous servir: vecteurs colinéaux

3Y³ + et² - y = -9xy² et '+ 2 et' + x et '

Le facteur commun et «dans le bon membre de l'égalité sont extraits

3Y³ + et² - y = y '(-9xy² + x + 2)

Enfin, le terme qui se multiplie et '. Obtenant ainsi l'expression correspondant à la dérivée implicite de y concernant x.

et '= dy / dx = (3y³ + et² - y) / (- 9xy² + x + 2)

Règle de la chaîne

Dans la dérivation implicite, la règle de la chaîne est toujours respectée. Toutes les expressions différentielles seront données en fonction de la variable indépendante x. De sorte que toute variable θ différente de x doit inclure le terme dθ / dx après avoir été dérivé.

Ce terme n'apparaîtra qu'au premier degré ou avec un exposant égal à 1. Cette qualité le rend complètement clairement sous les méthodes de factorisation traditionnelles. De sorte qu'il devient possible d'obtenir l'expression qui définit le différentiel dθ / dx.

Dans la règle de la chaîne, la nature progressive du processus de différenciation ou de dérivé est montrée. Où pour toute fonction composite f [g (x)], l'expression différentielle de f devra être

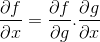
Ordre opérationnel

Dans chaque formule ou loi de dérivation appliquée, l'ordre des variables doit être pris en compte. Les critères associés à la variable indépendante sont respectés, sans modifier sa corrélation avec la variable dépendante.

Le rapport de la variable dépendante au moment de la dérive est prise directement.; À l'exception que cela sera considéré comme une deuxième fonction, c'est pourquoi les critères de règle de la chaîne pour les fonctions mixtes sont appliqués.

Cela peut être développé en expressions avec plus de 2 variables. Selon les mêmes principes.

Peut vous servir: quelle est la directive? (Géométrie)

Graphiquement, les mêmes critères sont gérés qui définissent le dérivé. Alors que la dérivée est la pente de la ligne tangente à la courbe du plan, le reste des différentiels appartenant aux variables dépendantes (Dy / Dx, DZ / DX) représentent des plans tangents aux corps vectoriels décrits par les fonctions de variable multiple variable.

Implicite d'une fonction

On dit qu'une fonction est implicitement définie, si l'expression y = f (x) peut être représentée comme une fonction variable multiple f (x, y) = 0 tandis que f est défini dans le plan r².

3xy³ - 2y + xy² = x et peut être écrit sous la forme 3xy³ - 2y + xy² - Xy = 0

Compte tenu de l'impossibilité d'expliquer la fonction y = f (x).

Histoire

Le calcul différentiel a commencé à être nommé par divers chercheurs mathématiques, vers le XVIIe siècle. La première fois qu'il a été mentionné, c'était par le biais des contributions de Newton et Leibniz. Les deux ont traité le calcul différentiel à partir de différents points de vue, mais convergeant dans leurs résultats.

Alors que Newton s'est concentré sur la différenciation en tant que vitesse de vitesse ou de variation, l'approche Leibniz était plus géométrique. On peut dire que Newton a attaqué les conjectures laissées par Apollonius de Perge et Leibniz les idées géométriques de Fermat.

La dérivation implicite apparaît immédiatement lorsque les équations différentielles et complètes considèrent. Ils ont étendu le concept géométrique de Leibniz à R³ et même des espaces multidimensionnels.

Applications

Les dérivés implicites sont utilisés dans diverses situations. Ils sont communs dans les problèmes de taux de change entre les variables connexes, où, selon le sens de l'étude, les variables seront considérées comme dépendantes ou indépendantes.

Ils ont également des applications géométriques intéressantes, comme dans les problèmes de réflexions ou d'ombres, sur des figures dont la forme peut être modélisée mathématiquement.

Peut vous servir: échantillonnage de quota: méthode, avantages, inconvénients, exemples

Ils sont fréquents dans les domaines de l'économie et de l'ingénierie, ainsi que dans diverses recherches sur les phénomènes naturels et les bâtiments expérimentaux.

Exercices résolus

Exercice 1

Définissez l'expression implicite qui définit DY / DX

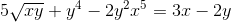
Chaque élément est différent de l'expression

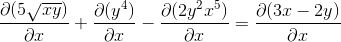
Établir la règle de la chaîne dans chaque cas compétent

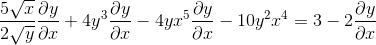
Regroupant d'un côté de l'égalité les éléments qui ont dy / dx

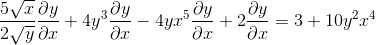
L'affectation utilise-t-elle le facteur commun

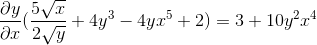
Est éliminé en obtenant l'expression recherchée

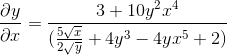
Exercice 2

Définissez l'expression implicite qui définit DY / DX

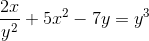
Exprimant les dérivés à réaliser

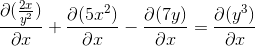
Dérivant implicitement selon la règle de la chaîne

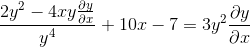
Prise en compte des éléments communs

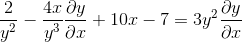
Regroupant le terme dy / dx d'un côté de l'égalité

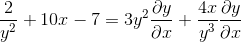
Facteur commun à l'élément différentiel

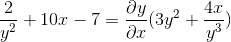
Nous effacons et obtenons l'expression recherchée

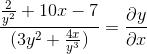
Les références

1. Calcul d'une seule variable. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 novembre. 2008
2. Le théorème de la fonction implicite: histoire, théorie et applications. Steven G. Krantz, Harold R. Parcs. Springer Science & Business Media, 9 novembre. 2012
3. Analyse multivariée. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 décembre. 2010
4. Dynamique du système: modélisation, simulation et contrôle des systèmes mécatroniques. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mars. 2012
5. Calcul: mathématiques et modélisation. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1er janvier. 1999